|
|
|
|
|
|
|
  |
 Jul 19 2014, 02:32 PM Jul 19 2014, 02:32 PM
Publicado:
#11
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente.
-------------------- |
|
|
|
 Jul 19 2014, 02:35 PM Jul 19 2014, 02:35 PM
Publicado:
#12
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 12-2 Control 3 Semestre Pimavera 2012
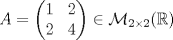 . Considere la función . Considere la función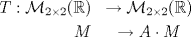 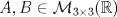 dadas por dadas por![TEX: \[A=\begin{pmatrix}<br />1&1&0\\<br />0&1&1\\<br />0&0&1<br />\end{pmatrix},\quad\begin{pmatrix}<br />1&1&0\\<br />1&1&0\\<br />0&0&1<br />\end{pmatrix}\]](/tex-image/9643bdca80d1751d898c0c683957bc27.png) Para cada una de ellas se pide los siguiente: Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 21 2014, 10:50 AM -------------------- |
|
|
|
 Jul 19 2014, 02:36 PM Jul 19 2014, 02:36 PM
Publicado:
#13
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente.
-------------------- |
|
|
|
 Jul 19 2014, 02:38 PM Jul 19 2014, 02:38 PM
Publicado:
#14
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 13-2 Control 3 Semestre Pimavera 2013
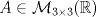 una matriz simétrica. Se sabe que el polinomio característico de A es una matriz simétrica. Se sabe que el polinomio característico de A es 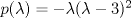 y que (1,-1,0) y (1,1,-2) son vectores proprios de A asociados al valor propio y que (1,-1,0) y (1,1,-2) son vectores proprios de A asociados al valor propio 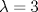 . Se pide construir la matriz A. . Se pide construir la matriz A.b) (3,0 ptos.) Considere la matriz 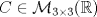 definida por definida por![TEX: \[\begin{pmatrix}<br />2&a&0\\<br />0&2&b\\<br />0&0&2<br />\end{pmatrix}\]](/tex-image/f515a4de3cd0ffdd44788a611fc0023b.png) ¿Para qué valores de a y b en IR la matriz C es diagonalizable? Jutifique su respuesta. 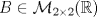 , considere la transformación lineal , considere la transformación lineal 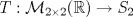 definida por definida por![TEX: \[T(X)=BX+X^TB^T\]](/tex-image/24fe6e28ca93ef75a8249a23843eab23.png) donde ![TEX: \[X=\begin{pmatrix}<br />x_1&x_2\\<br />x_3&x_4<br />\end{pmatrix}\in\mathcal{M}_{2\times 2}(\mathbb{R})\]](/tex-image/f900bba357cc768ac6d30c3cf923a5d8.png)
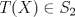 . .b) (3,0 ptos.) Para 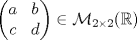 encuentre la matriz representante de T con respecto a la base canónica de encuentre la matriz representante de T con respecto a la base canónica de 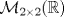 y la base y la base![TEX: \[\left\{\begin{pmatrix}<br />1&0\\<br />0&1\end{pmatrix},\ \begin{pmatrix}<br />0&1\\<br />1&0\end{pmatrix},\ \begin{pmatrix}<br />0&0\\<br />0&1\end{pmatrix}\right\}\]](/tex-image/6dcf1b5d39c9cc69f9e83693c44a3b23.png) de S2. c) (2,0 ptos.) Para 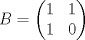 encuentre bases y dimensión para ker(T) e Im(T). encuentre bases y dimensión para ker(T) e Im(T).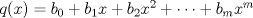 un polinomiode grado m y A una matriz cuadrada. Se define un polinomiode grado m y A una matriz cuadrada. Se define![TEX: \[q(A)=b_0I+b_1A+b_2A^2+\dots+b_mA^m\]](/tex-image/01b852b86a598b92a95e44d4c62fed7f.png) Si 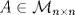 es una matriz diagonalizable, es una matriz diagonalizable, 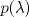 su polinomio característico y A=PDP-1, su diagonalización, se pide: su polinomio característico y A=PDP-1, su diagonalización, se pide:Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 21 2014, 11:07 AM -------------------- |
|
|
|
 Jul 19 2014, 02:46 PM Jul 19 2014, 02:46 PM
Publicado:
#15
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 14-1 Control 3 Semestre Pimavera 2014
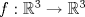 la tranformación lineal definida por la tranformación lineal definida por![TEX: \[f(x,y,z)=(-x-2y+2z,-y,-x-3y-4z)\]](/tex-image/f89cf0f2f3dda3af7ab387fa4049c0e5.png)
b) (2,0 ptos.) Calcular ![TEX: \[\begin{pmatrix}<br />-1&-2&2\\<br />0&-1&0\\<br />-1&-3&-4\end{pmatrix}^n\]](/tex-image/9b0e1dea84e72068bde3ad22550f9134.png) c) (2,0 ptos.) ¿Existe una matriz P tal que 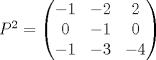 ? De existir encuéntrela, de lo contrario justifique claramente su respuesta. ? De existir encuéntrela, de lo contrario justifique claramente su respuesta.
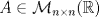 es igual a es igual a 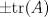 , donde tr(A) es la traza de la matriz A. Concluya que la traza es igual a la suma de los valores propios de la matriz. , donde tr(A) es la traza de la matriz A. Concluya que la traza es igual a la suma de los valores propios de la matriz.b) (3,0 ptos.) Sea 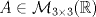 , diagonalizable con tr(A)=-4. Calcular los valores propios de A sabiendo que los valores propios de A2+2A son -1, 3 y 8. , diagonalizable con tr(A)=-4. Calcular los valores propios de A sabiendo que los valores propios de A2+2A son -1, 3 y 8.c) (1,0 pto.) Sea 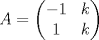 . Decida para qué valores de k la matriz es diagonalizable sobre IR, y para cuáles no lo es. . Decida para qué valores de k la matriz es diagonalizable sobre IR, y para cuáles no lo es.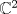 como un espacio vectorial sobre IR. Sea como un espacio vectorial sobre IR. Sea 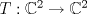 la transformación lineal dada por la transformación lineal dada por![TEX: \[T(x_1,x_2)=(2x_1-ix_2,x_1+x_2)\]](/tex-image/85c819502d14c1c871be6dfe6da3ce10.png) Sean B={(1,0),(0,1),(i,0),(0,i)} y B'={(1,i),(1,-i),(i,1),(i,-1)}.
b) (3,0 ptos.) Calcule, usando a) y matrices de cambio de base, las matrices representantes de la transformación lineal, TB'B, TBB', TB'B'. Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 19 2014, 02:47 PM -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:51 PM |





![TEX: \[\forall u,v \in \mathbb{R}^n, (u\cdot v)^2\leq\|u\|^2\|v\|^2\]](/tex-image/283098445a030208c5fa871145b851c6.png) Cauchy y Schwarz... Y Bun...
Cauchy y Schwarz... Y Bun...
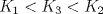 ???[/juice]
???[/juice]


![TEX: \[\beta = \left\{\begin{pmatrix}<br />1&0\\<br />0&0<br />\end{pmatrix},\begin{pmatrix}<br />0&1\\<br />0&0<br />\end{pmatrix},\begin{pmatrix}<br />0&0\\<br />1&0<br />\end{pmatrix},\begin{pmatrix}<br />0&0\\<br />0&1<br />\end{pmatrix}\right\}\]](/tex-image/38bbe4896c69a23e3ac58f7d15adaa62.png)
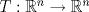 una función lineal tal que
una función lineal tal que 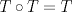 .Pruebe que
.Pruebe que 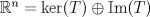 .
.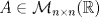 tiene sólo un valor propio igual a 1 y es diagonalizable, entonces A=I.
tiene sólo un valor propio igual a 1 y es diagonalizable, entonces A=I.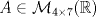 y
y 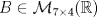 . Muestre que B·A no puede ser la identidad
. Muestre que B·A no puede ser la identidad 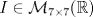
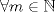 Am es combinción lineal de I, A, A2,...,An-1.
Am es combinción lineal de I, A, A2,...,An-1.