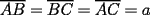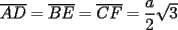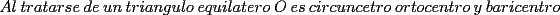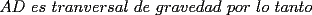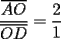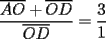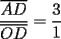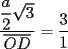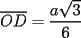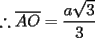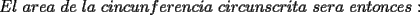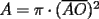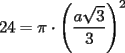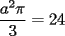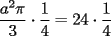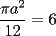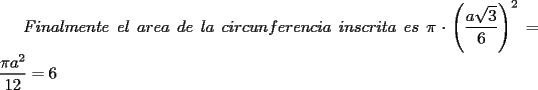Fecha 2. CEMAT 2007. VIII Región,.M3 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2007 > Segunda Fecha

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Fecha 2. CEMAT 2007. VIII Región,.M3, Individual

Joaquito Ver Perfil del Miembro Ver los mensajes de este miembro	May 12 2007, 11:20 PM Publicado: #1
Matemático Grupo: Usuario FMAT Mensajes: 54 Registrado: 21-April 07 Miembro Nº: 5.372 Nacionalidad: Sexo:	Prueba Individual: $TEX: Una "terna pitagorica" es una terna de numeros enteros positivos (a,b,c) tales que $a^2 + b^2 = c^2$. Ejemplos de ternas pitagoricas son (3,4,5), (5,12,13) y (6,8,10).<br /><br />Notese que si se divide por 2 los terminos de la tercera terna pitagorica de arriba, se obtiene la primera. Una "terna pitagorica primitiva" es una terna pitagorica cuyos 3 terminos no tienen un divisor comun mayor que 1. Asi, las 2 primeras ternas pitagorica de arriba son primitivas, pero la tercera no lo es.$ Problema 1 $TEX: Sean p,q enteros positivos con $p>q$. Demostrar que los numeros $a = p^2 - q^2$, $b = 2pq$ y $c= p^2 + q^2$ forman una terna pitagorica.<br /><br />Problema 2: La figura muestra un triangulo equilatero, con sus circunferencias circunscrita e inscrita (mayor y menor).$ [imágen aquí] $TEX: Si el area de la circ. circunscrita es 24, encontrar el area de la circ. inscrita.<br /><br />Problema 3: Sean p,q enteros positivos con $p>q$. Suponer que uno de ellos es impar y el otro par, y que su unico divisor comun es 1. Demostrar que los numeros $a = p^2 - q^2$, $b = 2pq$ y $c = p^2 + q^2$ forman una terna pitagorica primitiva.$ Eso No se puede poner tildes =\ Primer post . Archivo(s) Adjunto(s) olimp.JPG ( 7.17k ) Número de descargas: 1

Joaquito Ver Perfil del Miembro Ver los mensajes de este miembro	May 12 2007, 11:35 PM Publicado: #2
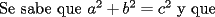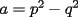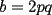Matemático Grupo: Usuario FMAT Mensajes: 54 Registrado: 21-April 07 Miembro Nº: 5.372 Nacionalidad: Sexo:	Bueno, mi solución del 1 es: 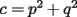$TEX: Se sabe que $a^2 + b^2 = c^2$ y que$ $TEX: $a = p^2 - q^2$$ $TEX: $b = 2pq$$ $TEX: $c= p^2 + q^2$$ Entonces, debería cumplirse que: 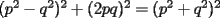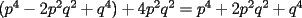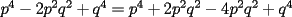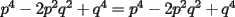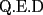$TEX: $(p^2 - q^2)^2 + (2pq)^2 = (p^2 + q^2)^2$$ $TEX: $(p^4 - 2p^2q^2 + q^4) + 4p^2q^2 = p^4 + 2p^2q^2 + q^4$$ $TEX: $p^4 - 2p^2q^2 + q^4 = p^4 + 2p^2q^2 - 4p^2q^2 + q^4$$ $TEX: $p^4 - 2p^2q^2 + q^4 = p^4 - 2p^2q^2 + q^4$$ $TEX: Q.E.D$

Aprendixmat Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 12:39 AM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 512 Registrado: 28-November 06 Miembro Nº: 3.014 Nacionalidad: Universidad: Sexo:	sorry por el condoro... Mensaje modificado por Aprendixmat el May 13 2007, 04:24 PM

keyno Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 01:13 AM Publicado: #4
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 25 Registrado: 31-March 06 Desde: chillan Miembro Nº: 738	Creo que la respuesta esta erronea. ya que la solución es 6 Solución Como el área es 24 tenemos que el radio de la circunferencia circunscrita es R=sqrt(24/Pi), luego como sabemos que el centro de la circuferencia inscrita coincide con la de la circunferencia circunscrita tenemos que 2OF=OC, entonces el radio de la circunsferencia inscrita es r=\frac{1}{2}\cdot \sqrt(frac{24}{Pi})=sqrt(frac{6}{Pi}). por lo tanto el área es 6.

keyno Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 01:18 AM Publicado: #5
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 25 Registrado: 31-March 06 Desde: chillan Miembro Nº: 738	FELICITO A LOS MONITORES YA QUE ESTA FECHA SE NOTO MAS ORGANIZACIÓN DE ELLOS, LO QUE SE VIO REFLEJADO A LA HORA DE COMENZAR CON LAS PRUEBAS

mical_alex Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 12:36 PM Publicado: #6
Principiante Matemático Grupo: Usuario FMAT Mensajes: 6 Registrado: 24-August 06 Desde: Concepcion Miembro Nº: 2.037 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	si la solucion de la 2, era 6

ciunhaly Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 02:45 PM Publicado: #7
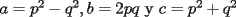Maestro Matemático Grupo: Colaborador Silver Mensajes: 128 Registrado: 30-June 06 Desde: En Rio de Janeiro, Brasil Miembro Nº: 1.477 Nacionalidad: Universidad: Sexo:	Joaquito, discuto con tu forma de resolver el problema 1, pues por lo que te pide la pregunta es si $TEX: $a=p^2-q^2, b=2pq$ y $c=p^2+q^2$$ entonces cumple una terna pitagórica. Lo que tú haces es partir de lo que se pide demostrar, no está mal tu razonammiento, pero por que no mejor ser más estricto y partir de la hipótesis. -------------------- _______________________________________________________________ "La primera regla de la enseñanza es saber lo que se debe enseñar. La segunda, es saber un poco más de aquello que se debe enseñar". George Polya Eu sou uma estudante da UFRJ.

Joaquito Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 04:37 PM Publicado: #8
Matemático Grupo: Usuario FMAT Mensajes: 54 Registrado: 21-April 07 Miembro Nº: 5.372 Nacionalidad: Sexo:	No entendí . ¿Cómo así? En fin, mi solución del 2 es esta: Solución problema 2 llamé: r: Radio circ. circunscrito. a: Radio circ. inscrito. At: Área triángulo Atr: Área Triángulos rectángulos x: Área circ. inscrito A: Área circ. cinscunscrito = 24 h: altura triángulo equilátero. b: base del mismo p: pi Lo que había que hacer era calcular a. y para ello había que calcular h y r, debido a que, lógicamente: 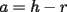$TEX: $a= h - r$$ Ya, lo que hice yo fue, en vez de calcular, dividí el triángulo equilátero en seis triángulos rectángulos iguales 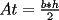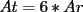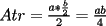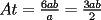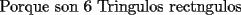; como muestra la figura. Tenemos que: $TEX: $At = \frac{bh}{2}$$ $TEX: $At = 6Ar$$ $TEX: $Atr = \frac{a\frac{b}{2}}{2} = \frac{ab}{4}$$ $TEX: $At = \frac{6ab}{a} = \frac{3ab}{2}$$ $TEX: Porque son 6 Triángulos rectángulos$ Igualamos 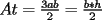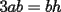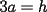$TEX: $At = \frac{3ab}{2} = \frac{bh}{2}$$ $TEX: $3ab = bh$$ $TEX: $3a = h$$ Bien, ahora aplico la fórmula y igualamos. 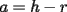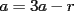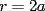$TEX: $a= h - r$$ $TEX: $a= 3a - r$$ $TEX: $r= 2a$$ Después, tenemos que: 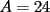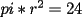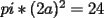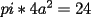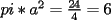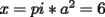$TEX: $A = 24$$ $TEX: $pir^2 = 24$$ $TEX: $pi(2a)^2 = 24$$ $TEX: $pi4a^2 = 24$$ $TEX: $pia^2 = \frac{24}{4} = 6$$ $TEX: $x = pia^2 = 6$$ Ahí está . Forma extraña quizás pero llegué al resultado =\ Archivo(s) Adjunto(s)* Dibujo.JPG ( 7.98k ) Número de descargas: 2

Joaquito Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 04:51 PM Publicado: #9
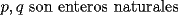Matemático Grupo: Usuario FMAT Mensajes: 54 Registrado: 21-April 07 Miembro Nº: 5.372 Nacionalidad: Sexo:	Bueno y esta es mi solución para el 3, que no sé si estará tan buena tampoco =\ pero en fin: 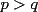$TEX: $p,q$ son enteros naturales$ $TEX: $p>q$$ Uno es par y el otro impar. Su único divisor común es 1 Se demostró en el Problema 1 que: 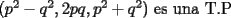$TEX: $(p^2 - q^2, 2pq, p^2 + q^2)$ es una T.P$ Se nos muestra que: 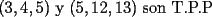$TEX: $(3,4,5)$ y $(5,12,13)$ son T.P.P$ Deducimos a partir de esto que : a,c son impares y b es par en una T.P.P. Y se nos dice también que el divisor común en una T.P.P no puede ser mayor que uno. Se cumple lo último, por lo que sólo hay que probar que b sea par. (si fueran a,c pares, 2 sería divisor común) 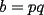$TEX: $b = pq$$ y si p,q son enteros positivos, p*q también; y como se cumple que 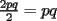$TEX: $\frac{2pq}{2} = pq$$ b es par. Q.E.D Vago quizás pero no recuerdo qué más puse .

Aprendixmat Ver Perfil del Miembro Ver los mensajes de este miembro	May 13 2007, 05:16 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 512 Registrado: 28-November 06 Miembro Nº: 3.014 Nacionalidad: Universidad: Sexo:	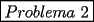$TEX: $\boxed{Problema\ 2}$$ Esta es mi solución: $TEX: $\overline{AB}=\overline{BC}=\overline{AC}=a$$ $TEX: $\overline{AD}=\overline{BE}=\overline{CF}=\dfrac{a}{2}\sqrt{3}$$ $TEX: $Al\ tratarse\ de\ un\ triangulo\ equilatero\ O\ es\ circuncetro\ ortocentro\ y\ baricentro$$ $TEX: $AD\ es\ tranversal\ de\ gravedad\ por\ lo\ tanto$$ $TEX: $\dfrac{\overline{AO}}{\overline{OD}}=\dfrac{2}{1}$$ $TEX: $\dfrac{\overline{AO}+\overline{OD}}{\overline{OD}}=\dfrac{3}{1}$$ $TEX: $\dfrac{\overline{AD}}{\overline{OD}}=\dfrac{3}{1}$$ $TEX: $\dfrac{\dfrac{a}{2}\sqrt{3}}{\overline{OD}}=\dfrac{3}{1}$$ $TEX: $\overline{OD}=\dfrac{a\sqrt{3}}{6}$$ $TEX: $\therefore \overline{AO}=\dfrac{a\sqrt{3}}{3}$$ $TEX: $El\ area\ de\ la\ cincunferencia\ circunscrita\ sera\ entonces:$$ $TEX: $A=\pi\cdot (\overline{AO})^2$$ $TEX: $24=\pi \cdot \left(\dfrac{a\sqrt{3}}{3}\right)^2$$ $TEX: $\dfrac{a^2\pi}{3}=24$$ $TEX: $\dfrac{a^2\pi}{3}\cdot \dfrac{1}{4}=24\cdot \dfrac{1}{4}$$ $TEX: $\dfrac{\pi a^2}{12}=6$$ $TEX: $Finalmente\ el\ area\ de\ la\ circunferencia\ inscrita\ es\ \pi\cdot \left(\dfrac{a\sqrt{3}}{6}\right)^2=\dfrac{\pi a^2}{12}=6$$ Agradezco a Gp20 por haber notado mi error xDDD Saludos Mensaje modificado por Aprendixmat el May 13 2007, 11:49 PM

« Posterior · Segunda Fecha · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 07:54 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.