duda sobre demostracion de tautologias

duda sobre demostracion de tautologias

Opciones

Caotico Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2014, 04:45 PM Publicado: #1
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 8-April 08 Miembro Nº: 19.425 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Necesito demostrar que (p ⇒ q) ⇒ [(∼ q) ⇒ (∼ p)] es una tautologia, pero la verdad es que no tengo idea de como se demuestra un tautologia (tengo un profe super bueno jajaja). Ayuda por favor (Sin tablas de verdad) Mensaje modificado por Caotico el Apr 19 2014, 05:32 PM

holder14 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2014, 06:47 PM Publicado: #2
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 5-April 14 Miembro Nº: 128.324 Sexo:	CITA(Caotico @ Apr 19 2014, 04:45 PM) Necesito demostrar que (p ⇒ q) ⇒ [(∼ q) ⇒ (∼ p)] es una tautologia, pero la verdad es que no tengo idea de como se demuestra un tautologia (tengo un profe super bueno jajaja). Ayuda por favor (Sin tablas de verdad) probaste llevando los implica a conectivos más débiles? p => q es equivalente a ¬p o q

Caotico Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2014, 07:01 PM Publicado: #3
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 8-April 08 Miembro Nº: 19.425 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Si, pero me refiero a como deberia quedar, por ejemplo llego a ((¬p) o q) ⇒ (q o (¬p)). Quedaria asi o hay que hacer algo mas?

samuelfuentes Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2014, 08:01 PM Publicado: #4
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 18-September 13 Miembro Nº: 122.509 Nacionalidad: Sexo:	¿Podría ser así? 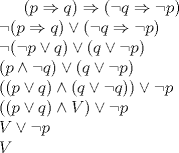$TEX: <br />$(p\Rightarrow q)\Rightarrow(\neg q\Rightarrow\neg p)\\<br />\neg(p\Rightarrow q)\vee(\neg q\Rightarrow\neg p)\\<br />\neg(\neg p\vee q)\vee(q\vee\neg p)\\<br />(p\wedge\neg q)\vee(q\vee\neg p)\\<br />((p\vee q)\wedge (q\vee\neg q))\vee\neg p\\<br />((p\vee q)\wedge V)\vee\neg p\\<br />V\vee\neg p\\<br />V$<br />$ Mensaje modificado por samuelfuentes el Apr 19 2014, 08:24 PM

samuelfuentes Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 19 2014, 08:24 PM Publicado: #5
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 18-September 13 Miembro Nº: 122.509 Nacionalidad: Sexo:	CITA(samuelfuentes @ Apr 19 2014, 09:01 PM) ¿Podría ser así? $TEX: <br />$(p\Rightarrow q)\Rightarrow(\neg q\Rightarrow\neg p)\\<br />\neg(p\Rightarrow q)\vee(\neg q\Rightarrow\neg p)\\<br />\neg(\neg p\vee q)\vee(q\vee\neg p)\\<br />(p\wedge\neg q)\vee(q\vee\neg p)\\<br />((p\vee q)\wedge (q\vee\neg q))\vee\neg p\\<br />((p\vee q)\wedge V)\vee\neg p\\<br />V\vee\neg p\\<br />V$<br />$ Estaba malo el final =/ $TEX: <br />$(p\Rightarrow q)\Rightarrow(\neg q\Rightarrow\neg p)\\<br />\neg(p\Rightarrow q)\vee(\neg q\Rightarrow\neg p)\\<br />\neg(\neg p\vee q)\vee(q\vee\neg p)\\<br />(p\wedge\neg q)\vee(q\vee\neg p)\\<br />((p\vee q)\wedge (q\vee\neg q))\vee\neg p\\<br />((p\vee q)\wedge V)\vee\neg p\\<br />(p\vee q)\vee\neg p\\<br />(p\vee\neg p)\vee q)\\<br />V\vee q\\<br />V$<br />$ Mensaje modificado por samuelfuentes el Apr 19 2014, 08:24 PM

holder14 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 20 2014, 08:39 PM Publicado: #6
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 5-April 14 Miembro Nº: 128.324 Sexo:	CITA(samuelfuentes @ Apr 19 2014, 08:24 PM) Estaba malo el final =/ 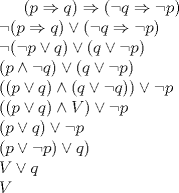$TEX: <br />$(p\Rightarrow q)\Rightarrow(\neg q\Rightarrow\neg p)\\<br />\neg(p\Rightarrow q)\vee(\neg q\Rightarrow\neg p)\\<br />\neg(\neg p\vee q)\vee(q\vee\neg p)\\<br />(p\wedge\neg q)\vee(q\vee\neg p)\\<br />((p\vee q)\wedge (q\vee\neg q))\vee\neg p\\<br />((p\vee q)\wedge V)\vee\neg p\\<br />(p\vee q)\vee\neg p\\<br />(p\vee\neg p)\vee q)\\<br />V\vee q\\<br />V$<br />$ cuando te piden demostrar una tautologia, usando tablas de verdad, todos saben que la columna debe ser siempre verdadera, sin usar tablas, la idea es usar los teoremas y deberiamos llegar siempre a V asi que yo opino que tu desarrollo es correcto, aunque sinceramente no lo revise paso a paso... pero la idea es esa, llevar a lo basico y obtener verdadero, esto implica que el valor de verdad de la proposicion compuesta inicial, es valida independiente del valor de verdad de cada proposicion basica o simple.

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 12th April 2025 - 06:54 AM