|
|
|
|
|
|
|
  |
 Feb 23 2014, 04:20 PM Feb 23 2014, 04:20 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 23-February 14 Miembro Nº: 127.090 Nacionalidad:  Sexo:  |
Gracias Mensaje modificado por CARLOS04 el Feb 23 2014, 04:30 PM
Archivo(s) Adjunto(s)
|
|
|
|
 Feb 23 2014, 06:07 PM Feb 23 2014, 06:07 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Observaciones:
Para lo que te hace falta del b, utiliza el siguiente hecho más general: Sea G un grupo. Si N es subgrupo normal de G y M es subgrupo característico de N, entonces M es subgrupo normal de G. (El subgrupo H que pones es subgrupo normal de G y tú demostraste que el r-subgrupo de Sylow de H es un subgrupo característico de H...) -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Feb 23 2014, 06:18 PM Feb 23 2014, 06:18 PM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 23-February 14 Miembro Nº: 127.090 Nacionalidad:  Sexo:  |
Gracias por responder, pero ¿si están correctas las otras partes del ejercicio?, muchisimas gracias
|
|
|
|
 Feb 23 2014, 06:28 PM Feb 23 2014, 06:28 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
¿Cómo deduces que de
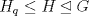 se sigue que se sigue que 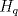 es normal en G? Tú afirmación es correcta pero pudieras estar derivándola a partir de una idea errónea. es normal en G? Tú afirmación es correcta pero pudieras estar derivándola a partir de una idea errónea.Por cierto, ya chequé el inciso a también... Todo bien ahí . -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Feb 23 2014, 06:48 PM Feb 23 2014, 06:48 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 23-February 14 Miembro Nº: 127.090 Nacionalidad:  Sexo:  |
|
|
|
|
 Feb 23 2014, 06:49 PM Feb 23 2014, 06:49 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Sí es por eso entonces no tengo más que agregar... Saludos.
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Feb 23 2014, 06:50 PM Feb 23 2014, 06:50 PM
Publicado:
#7
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 23-February 14 Miembro Nº: 127.090 Nacionalidad:  Sexo:  |
Muchas gracias por tu tiempo, una saludo.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:45 PM |









