Equivalencias del axioma del supremo

Equivalencias del axioma del supremo

Opciones

lapantufla Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 25 2014, 09:19 PM Publicado: #1
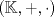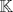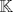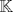Matemático Grupo: Usuario FMAT Mensajes: 52 Registrado: 5-December 12 Miembro Nº: 114.123 Nacionalidad: Sexo:	Sea $TEX: $(\mathbb{K},+,\cdot)$$ un cuerpo ordenado, pruebe que las siguientes proposiciones son equivalentes (1) Todo conjunto no vació y acotado superiormente tiene supremo en $TEX: $\mathbb{K}$$ (2) Toda sucesión creciente y acotada de elementos en $TEX: $\mathbb{K}$$ tiene limite en $TEX: $\mathbb{K}$$ (3) Toda sucesión acotada de elementos en 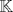$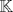TEX: $\mathbb{K}$$ tiene al menos un valor de adherencia en $TEX: $\mathbb{K}$$ (4) Se verifica el principio de los intervalos encajados y la propiedad arquimediana (5) Toda sucesión de Cauchy tiene limite en 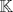$TEX: $\mathbb{K}$$ y se verifica la propiedad arquimediana No es necesario que hagan todo en un mismo post y si saben de otra equivalencia sería bueno que la compartan. Pueden ver para la definición y las equivalencias de la propiedad arquimediana.

Kasanizo Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 25 2014, 09:28 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 319 Registrado: 1-February 12 Desde: Providencia, Santiago Miembro Nº: 100.801 Nacionalidad: Universidad: Sexo:	Para la 4), esto lo subió san martín en el curso de cálculo diferencial PA_IE.Supremo1.jpg ( 201.94k ) Número de descargas: 21 PA_IE.Supremo2.jpg ( 180.73k ) Número de descargas: 13 Mensaje modificado por Kasanizo el Jan 25 2014, 09:29 PM -------------------- Cuidar la propia ortografía es una forma de respeto no sólo hacia los demás, sino que también hacia uno mismo.

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 04:39 PM