Equivalencias de la propiedad arquimediana

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Cálculo > Axiomas de Orden y Cuerpo

Equivalencias de la propiedad arquimediana

Opciones

Heiricar Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2014, 12:27 AM Publicado: #1
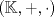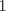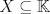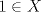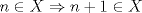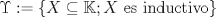Dios Matemático Grupo: Colaborador Silver Mensajes: 423 Registrado: 4-January 11 Miembro Nº: 82.624 Nacionalidad: Universidad: Sexo:	$TEX: $(\mathbb{K},+,\cdot )$$ sera un cuerpo ordenado con neutro multiplicativo $TEX: $1$$ Se dirá que un conjunto $TEX: $X\subseteq \mathbb{K}$$ es inductivo si $TEX: $1\in X$$ y $TEX: $n \in X \Rightarrow n+1 \in X$$ y se define $TEX: $$\Upsilon :=\{ X\subseteq \mathbb{K} ; X \ \text{es inductivo} \}$$$ Ahora se definen los conjuntos 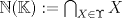$TEX: $\mathbb{N}(\mathbb{K}):=\bigcap_{X \in \Upsilon}X$$ y $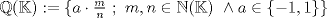TEX: $\mathbb{Q}(\mathbb{K}):=\{ a\cdot\frac{m}{n} \ ; \ m,n \in \mathbb{N}(\mathbb{K})\ \wedge a \in \{-1,1\} \}$$ . 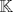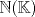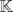Un cuerpo ordenado $TEX: $\mathbb{K}$$ se dirá que cumple la propiedad arquimediana si $TEX: $\mathbb{N}(\mathbb{K})$$ no posee cota superior en $TEX: $\mathbb{K}$$ . 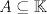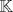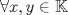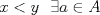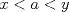$TEX: $A\subseteq \mathbb{K}$$ sera denso en $TEX: $\mathbb{K}$$ si $TEX: $\forall x,y \in \mathbb{K}$$ con $TEX: $x<y \ \ \exists a \in A$$ tal que $TEX: $x<a<y$$ . 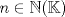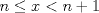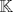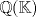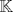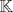Un numero $TEX: $n \in \mathbb{N}(\mathbb{K})$$ se dirá la parte entera de $TEX: $x$$ si $TEX: $n\leq x<n+1$$ Dadas estas definiciones demuestre que $TEX: $\mathbb{K}$$ cumple con la propiedad arquimediana si y solo si $TEX: $\mathbb{Q}(\mathbb{K})$$ es denso en $TEX: $\mathbb{K}$$ y si y solo si todo elemento mayor que 1 de $TEX: $\mathbb{K}$$ posee parte entera. Mensaje modificado por Heiricar el Jan 24 2014, 01:10 PM