Integral Doble 2 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Cálculo > Cálculo en Varias Variables

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Integral Doble 2, [Resuelto]

Julio_fmat Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 9 2013, 10:36 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	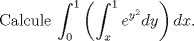$TEX: \noindent Calcule $\displaystyle \int_{0}^1\left(\displaystyle \int_{x}^1 e^{y^2}dy\right)dx.$$ $TEX: \noindent Esto estaba haciendo <br />\begin{eqnarray}<br />\displaystyle \int_{0}^1\left(\displaystyle \int_{x}^1 e^{y^2}dy\right)dx&=&\int_{x}^1\left(\int_{0}^1 e^{y^2}dx\right)dy\\<br />&=&\int_{x}^1\left(e^{y^2}\int_{0}^1 1dx\right)dy\\<br />&=&\left. \int_{x}^1\left(e^{y^2}x\right\|_0^1\right)dy\\<br />&=&\int_{x}^1 e^{y^2}dy<br />\end{eqnarray}<br />Y ahí ya no se me ocurre cómo integrar eso. Igual se que la integral debe de dar un número, y yo sólo he obtenido una función, ¿cómo se puede arreglar esto?<br />$ Mensaje modificado por Julio_fmat el Nov 15 2013, 06:52 PM -------------------- "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen. $TEX: $$\Phi=\displaystyle \int \limits_{-\infty}^x \dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}t^2}dt=\lim_{n\to +\infty}P\left(\dfrac{\displaystyle \sum_{i=1}^n x_i-n\mu}{n\sigma}\le x\right).$$$ Licenciado en Matemática (2021). Universidad de Concepción, Chile.

oza Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 9 2013, 11:37 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 653 Registrado: 24-October 08 Desde: valparaiso Miembro Nº: 36.938 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	como bien dices tiene que dar un numero , si cambias el orden de la integracion debes cambiar tambien los limites. como pasaste el dx adentro este variara de "0" a "y" mientras que el dy ira de "0" a "1" . Por lo menos a mi se me facilita mucho dibujando la region en la cual se integra con este cambio de orden se facilita la resolucion ya que finalmente se llega a una integral directa (se ve a simple vista) o simple sustitucion Mensaje modificado por oza el Nov 9 2013, 11:43 PM -------------------- Luis Egresado Ingeniería Civil Profesor Física Preusm Universidad Técnica Federico Santa María Casa Central Valparaíso Depto obras civiles

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 12:09 AM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	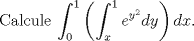CITA(Julio_fmat @ Nov 9 2013, 10:36 PM) $TEX: \noindent Calcule $\displaystyle \int_{0}^1\left(\displaystyle \int_{x}^1 e^{y^2}dy\right)dx.$$ $TEX: \noindent Esto estaba haciendo <br />\begin{eqnarray}<br />\displaystyle \int_{0}^1\left(\displaystyle \int_{x}^1 e^{y^2}dy\right)dx&=&\int_{x}^1\left(\int_{0}^1 e^{y^2}dx\right)dy\\<br />&=&\int_{x}^1\left(e^{y^2}\int_{0}^1 1dx\right)dy\\<br />&=&\left. \int_{x}^1\left(e^{y^2}x\right\|_0^1\right)dy\\<br />&=&\int_{x}^1 e^{y^2}dy<br />\end{eqnarray}<br />Y ahí ya no se me ocurre cómo integrar eso. Igual se que la integral debe de dar un número, y yo sólo he obtenido una función, ¿cómo se puede arreglar esto?<br />$ La integral de más afuera (de más a la izquierda) siempre tiene constantes en sus límites de integración. Dar vuelta las integrales así como así no lo puedes hacer. Lo que tienes que hacer es dibujarte tu región de integración, verificar cuáles son las funciones que acotan tu región, y con ella puedes hacer el cambio en el orden de integración. Si el orden de integración es dydx, significa que la integral de más afeura es con respecto a x, y ella se mueve entre 2 constantes. La integral de adentro es con respecto a y. Para conocer sus límites de integración, tira lineas imaginarias e abajo hacia arriba, y anda viendo con qué función chocas primero (límite inferior) y con qué función chocas después (límite superior). Esas funciones las tienes que colocar en el límite de integración con el 'y' despejado (porque la integral tiene dy). Dibuja la región de integración (te darás cuenta que es un triángulo acotado por las funciones x=0, y=1, y=x). Al cambiar el orden de integración a dxdy, entonces ahora en el eje y te mueves entre 2 cosntantes. Los límites de integración para la integral con dx, los ves tirando líneas imaginarias de izquierda a derecha, y ves con qué funcion chocas primero (límite inferior) y con qué función chocas después (límite superior). Si lo realizas bien, la integral te queda así: $TEX: <br /><br />\[ \int_{0}^{1}\int_{x}^{1} e^{y^2}dydx = \int_{0}^{1} \int_{0}^{y} e^{y^2} dxdy \]<br /><br />$

oza Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 12:23 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 653 Registrado: 24-October 08 Desde: valparaiso Miembro Nº: 36.938 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	stetwart varias variables -------------------- Luis Egresado Ingeniería Civil Profesor Física Preusm Universidad Técnica Federico Santa María Casa Central Valparaíso Depto obras civiles

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 11:23 AM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	Me tinca que no escribiste bien el problema porque wolfram me mordió cuando le pregunté. Mensaje modificado por Kaissa el Nov 10 2013, 11:33 AM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Coto-kun Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 11:32 AM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 427 Registrado: 5-October 10 Miembro Nº: 78.264 Nacionalidad: Universidad: Sexo:	te ayudaría, pero justo este lunes veo eso xd --------------------

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 12:15 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	CITA(Kaissa @ Nov 10 2013, 11:23 AM) Me tinca que no escribiste bien el problema porque wolfram me mordió cuando le pregunté. Está bien escrito. Cambiando el orden de integrción quedan integrales con primitivas elementales.

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 12:23 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Laðeralus @ Nov 10 2013, 12:15 PM) Está bien escrito. Cambiando el orden de integrción quedan integrales con primitivas elementales. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 12:33 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	CITA(Kaissa @ Nov 10 2013, 12:23 PM) Si trabajas con dydx: $TEX: <br />\[ \int_{0}^{1} \int_{x}^{1} e^{y^2}dydx = \frac{\sqrt{\pi}i}{2} \int_{0}^{1} \left( erf(ix)-erf(i) \right)dx = \frac{e-1}{2} \approx 0.859141 \]<br />$ (Cambiando el orden de integración) Si trabajas con dxdy: $TEX: <br />\[ \int_{0}^{1} \int_{x}^{1} e^{y^2}dydx = \int_{0}^{1} \int_{0}^{y} e^{y^2} dxdy = \int_{0}^{1} ye^{y^2} dy = \frac{e-1}{2} \]<br />$ Mensaje modificado por Laðeralus el Nov 10 2013, 12:36 PM

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2013, 12:42 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	Claro. Ahora, pa' explicárselo al Julio podríamos hacer lo siguiente: la integral de adentro se interpreta como desde y=x hasta y=1 con 0<x<1. Ese dominio es la región bajo la diagonal ascendente del cuadrado unitario con un vértice en el (0,0). Para integrarlo (o describirlo) primero con el eje X tendríamos que la X va desde el eje hasta la diagonal, es decir 0<x<y y finalmente 0<y<1. Ahí salen los límites de la segunda integral del Lander. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

« Posterior · Cálculo en Varias Variables · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 08:01 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.