|
|
|
|
|
|
|
  |
 Nov 4 2013, 09:43 PM Nov 4 2013, 09:43 PM
Publicado:
#1
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ok. Mismas reglas que en
Dudas, preguntas, aclaraciones, sugerencias por MP. Mensaje modificado por TribalJazz2 el Oct 17 2014, 10:25 AM -------------------- |
|
|
|
 Nov 4 2013, 09:48 PM Nov 4 2013, 09:48 PM
Publicado:
#2
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 07-2 Control 1 Semestre Primavera 2007
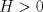 y radios superior y radios superior  e inferior e inferior 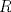 , donde , donde 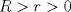 . De este árbol se desea tallar un cilindro de madera de base circular de modo de maximizar su volumen. Encuentre las dimensiones de este cilindro en téminos de los datos. . De este árbol se desea tallar un cilindro de madera de base circular de modo de maximizar su volumen. Encuentre las dimensiones de este cilindro en téminos de los datos.Atención: Dependiendo de los valores de  y y 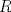 , pueden presentarse diferentes casos. , pueden presentarse diferentes casos.b) (3,0 ptos.) Un grupo de físicos se encuentra en la estación espacial chilena ”volantín" estudiando la órbita del cometa "UCHC2". Ellos han determinado que esta órbita es parabólica de ecuación 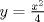 , tomando el origen en "volantín" y midiendo las longitudes en Unidades Astronómicas Apropiadas (UAA). En este mismo sistema, el sol está en la posición , tomando el origen en "volantín" y midiendo las longitudes en Unidades Astronómicas Apropiadas (UAA). En este mismo sistema, el sol está en la posición 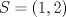 . Se sabe que por su composición química, "UCHC2" explotaría si su distancia al sol fuera menor o igual que 1 UAA. . Se sabe que por su composición química, "UCHC2" explotaría si su distancia al sol fuera menor o igual que 1 UAA.Para saber si el cometa explotará o no, se pide realizar lo siguiente: Escriba la distancia del cometa al sol en función de  , encuentre la menor distancia del cometa al sol y concluya si el cometa explotará o no. , encuentre la menor distancia del cometa al sol y concluya si el cometa explotará o no.
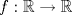 continua, con un mínimo global único en el punto continua, con un mínimo global único en el punto 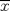 y que satisface y que satisface 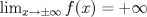 . Si . Si 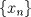 es una sucesión que tiene la propiedad es una sucesión que tiene la propiedad![TEX: \[\forall n\in\mathbb{N},\: f(x_n)\leq f(\overline{x})+\frac{1}{n}\]](/tex-image/8a85b832d464c244dc68cac374113c17.png) se pide: 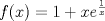 . Demuestre que existe un único . Demuestre que existe un único ![TEX: $x_0\in [-2,-1]$](/tex-image/7eb30e9652d1a8dd935b6cb45aa99f91.png) tal que tal que 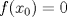 . .
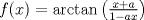 , donde , donde 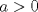 . Indique dónde . Indique dónde 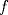 es continua y derivable, calcule es continua y derivable, calcule 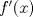 y pruebe que es independiente de y pruebe que es independiente de  . Aplique apropiadamente el TVM a la función . Aplique apropiadamente el TVM a la función 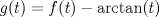 para deducir que para deducir que![TEX: \[\forall x\in \left.[0,\frac{1}{a}\right),\: f(x)=\arctan(x)+\arctan{a}\]](/tex-image/0c85debac154e319b593ca6e02ff5509.png) b) (3,0 ptos.) Sea 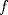 una función dos veces continuamente derivable en una función dos veces continuamente derivable en 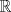 (es decir, con segunda derivada continua) y con (es decir, con segunda derivada continua) y con 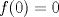 . Se define la función . Se define la función 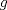 mediante la ley mediante la ley![TEX: \[g(x)=\begin{cases}<br />\frac{f(x)}{x} &\text{si } x\neq 0\\<br />f^\prime (0) &\text{si } x=0<br />\end{cases}\]](/tex-image/d619e3ca9f3aa03405c23275478b7013.png) Demuestre que la función 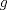 es continua, derivable, y con derivada continua en todo es continua, derivable, y con derivada continua en todo 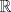 P1. P2. P3. Mensaje modificado por TribalJazz2 el May 18 2014, 02:14 PM -------------------- |
|
|
|
 Nov 4 2013, 09:58 PM Nov 4 2013, 09:58 PM
Publicado:
#3
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 08-1 Control 1 Semestre Otoño 2008
![TEX: $f:[a,b] \to \mathbb{R}$](/tex-image/f25773aaf2ebd9b7caa8b9cbc13a5dae.png) es una función continua, entonces es una función continua, entonces ![TEX: $\exists x_0 \in [a,b]$](/tex-image/b33fa64a3a69b23a8234147e858affca.png) tal que tal que ![TEX: \[f(x_0)=\frac{f(a)+f(b)}{2}\]](/tex-image/b0f96d4b037dd739bdd15294a4def7a6.png) b) Sea 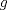 una función derivable en una función derivable en 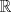 tal que tal que ![TEX: \[g(x)\cdot \tan x \geq 0, \quad \forall x\in\mathbb{R}\setminus \{k\pi + \frac{\pi}{2} : k \in \mathbb{Z}\}\]](/tex-image/0e86ce1a4a4459559ff9e64624e5d613.png) Demuestre que 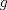 posee ceros en cada intervalo de la forma posee ceros en cada intervalo de la forma 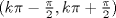 donde donde 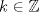 , y por lo tanto su derivada se anula infinitas veces. , y por lo tanto su derivada se anula infinitas veces.c) Una función 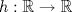 es derivable, con es derivable, con 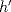 continua y satisface continua y satisface 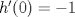 . Demuestre que existe . Demuestre que existe 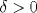 tal que tal que![TEX: \[\forall x\in (-\delta, \delta)\setminus \{ 0 \}\quad (h(x)-h(0))\cdot x< 0\]](/tex-image/7722ccaef11569602fcfb5b4df5a2191.png) 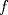 tal que tal que 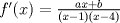
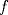 tiene una inflexión en tiene una inflexión en 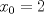 y que y que 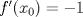 , calcule los valores de las constantes , calcule los valores de las constantes  y y  . .b) Determine los signos de 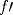 y y 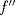 y concluya sobre los crecimientos y convexidades de y concluya sobre los crecimientos y convexidades de 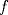 . Bosqueje el gráfico de . Bosqueje el gráfico de 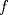 . .
![TEX: $\int x^3\sqrt[3]{x^2+1}\,dx$](/tex-image/92da78535219c9d6f30c2656ed6ef904.png) b) 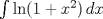 c) 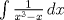 Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el May 18 2014, 01:55 PM -------------------- |
|
|
|
 Nov 4 2013, 10:04 PM Nov 4 2013, 10:04 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 08-2 Control 1 Semestre Primavera 2008
![TEX: \[f(x)=\begin{cases}\frac{2x^2}{x+a} & \text{si } x<a\\<br />2x-e^{x-a} & \text{si } x\geq a\end{cases}\]](/tex-image/bfa291861f300b1510e864cfcaba688f.png)
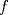 cuando cuando 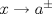 en términos de en términos de  , y pruebe que , y pruebe que 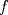 resulta ser continua en resulta ser continua en  si y solamente si si y solamente si 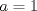 . .A partir de ahora considere que 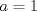 . .b) (1,0 pto.) Establezca el dominio de 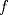 y el conjunto de puntos en los cuales y el conjunto de puntos en los cuales 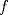 es continua. es continua.c) (1,0 pto.) Pruebe, usando TVI, que 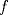 se anula en algún punto del intervalo se anula en algún punto del intervalo 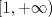 . .d) (1,0 pto.) Determine (si existen), asíntotas (horizontales, verticales, oblicuas). e) (1,0 pto.) Calcule 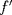 y determine puntos críticos, intervalos de crecimiento, máximos y mínimos. y determine puntos críticos, intervalos de crecimiento, máximos y mínimos.f) (1,0 pto.) Calcule 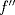 y determine convexidades, puntos de inflexión (si es que existen). y determine convexidades, puntos de inflexión (si es que existen).
![TEX: $f: [a,b]\to \mathbb{R}$](/tex-image/2cc4336bdb3236edd73ba5cd164b9a64.png) una función continua en una función continua en ![TEX: $[a, b]$](/tex-image/256546770e8f608499787e51a9f8274c.png) y dos veces derivable en y dos veces derivable en 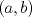 . Pruebe que si . Pruebe que si 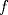 alcanza su máximo global en alcanza su máximo global en 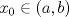 entonces, entonces, 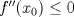 . .Ind: Use un desarrollo limitado de orden 2 de 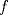 en torno a en torno a 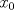 . .b) (2,0 ptos.) Sea ![TEX: $g: [0,1]\to \mathbb{R}$](/tex-image/670426d64f6bd47c3712d71a020ce89d.png) una función continua y dos veces derivable en una función continua y dos veces derivable en 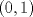 , la cual satisface , la cual satisface ![TEX: \[g^{\prime\prime} (x)= x^3 g(x)+g^2(x)g^\prime (x), \quad \forall x\in (0,1)\]](/tex-image/15a02d9f413ea284a7f4c0d83a9d2c15.png) Demuestre que si 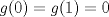 entonces entonces 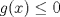 en todo en todo ![TEX: $[0,1]$](/tex-image/d00998eb5fb69732a2b31e3586b90dfd.png) . .Ind: Argumente por contradicción y use la parte (a) donde corresponda. c) (2,0 ptos.) Considere la función 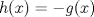 , donde , donde 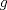 es la función de la parte (b). Verifique que es la función de la parte (b). Verifique que 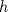 satisface las mismas hipótesis que la función satisface las mismas hipótesis que la función 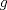 en (b), y use las conclusiones de (b) para deducir que en (b), y use las conclusiones de (b) para deducir que 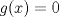 en todo en todo ![TEX: $[0, 1]$](/tex-image/0c360073928ac78b96d1cc7ab3e6be0d.png) . .
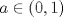 . Use el teorema del valor medio para demostrar que . Use el teorema del valor medio para demostrar que ![TEX: $\forall x\in (0,\frac{\pi}{2}]$](/tex-image/08250a9c6fdb937da84a75c95dac78bf.png) se cumple que se cumple que 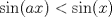 . Use esto para demostrar la siguiente desigualdad: . Use esto para demostrar la siguiente desigualdad:![TEX: \[(\cos x)^a \leq \cos (ax) \quad \forall x \in [0,\frac{\pi}{2}]\]](/tex-image/dca105a8ed2512078031ea7096935fe8.png) Ind: Estudie el crecimiento de la función 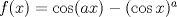 b) (3,0 ptos.) Sea 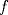 es una función infinitamente derivable en es una función infinitamente derivable en 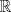 tal que tal que 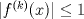 para todo para todo 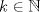 y y 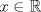 . Demuestre que si . Demuestre que si 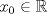 es fijo, entonces para todo es fijo, entonces para todo ![TEX: $x\in [x_0-1,x_0+1]$](/tex-image/0dd798f301531306cd1c0eaf414cf0ce.png) se cumple que se cumple que![TEX: \[\lim_{n\to\infty} \left| f(x)-T^{n}_{f} (x-x_0)\right | = 0\]](/tex-image/f5d3a6dac756e72f3a371d0cc30072a7.png) donde 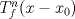 denota al polinomio de Taylor de denota al polinomio de Taylor de 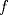 de orden de orden  en torno a en torno a 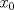 . .Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el May 18 2014, 02:15 PM -------------------- |
|
|
|
 Nov 5 2013, 06:42 AM Nov 5 2013, 06:42 AM
Publicado:
#5
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 09-1 Control 1 Semestre Otoño 2009
 y altura y altura 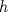 . Un insecto está localizado en el vértice . Un insecto está localizado en el vértice 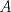 y debe llegar al vértice y debe llegar al vértice 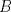 caminado en línea recta desde caminado en línea recta desde 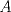 hasta hasta 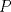 y de igual forma se desplaza desde y de igual forma se desplaza desde 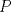 hasta hasta 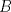 (ver figura). (ver figura).Determinar la posición del punto 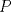 de manera de minimizar la distancia total recorrida. Justifique su de manera de minimizar la distancia total recorrida. Justifique surespuesta. Figura: P2.
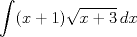 a.2) (2,0 ptos.) 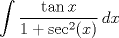 ![TEX: \[I_n=\int (x+1)^n \sin (2x)\, dx\]](/tex-image/00fd02874e3e7ad61125dea7decb2711.png)
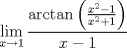 a.2) (1,0 pto.) 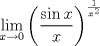 ![TEX: $f:[a,b]\to\mathbb{R},\ 0<a<b$](/tex-image/eb621af3fbd3132712b65c2651ed9fe6.png) , continua en , continua en ![TEX: $[a,b]$](/tex-image/cd5e80aef5bbdd2b93271ddb21b5658a.png) y diferenciable en y diferenciable en 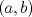 . Demuestre que si . Demuestre que si 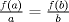 , entonces , entonces 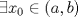 tal que tal que![TEX: \[x_0 f^\prime (x_0)=f(x_0)\]](/tex-image/64d8bf4df24a84688ad92284dee8bb82.png) c) (2,0 ptos.) Considere la función 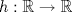 definida por definida por![TEX: \[h(x)=x^{13}+7x^3-5\]](/tex-image/bf1ae459cb1504f292fa048d63c8cee6.png) Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el May 18 2014, 02:22 PM -------------------- |
|
|
|
 Nov 5 2013, 06:43 AM Nov 5 2013, 06:43 AM
Publicado:
#6
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 09-2 Control 1 Semestre Primavera 2009
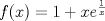 . Se pide: . Se pide:![TEX: $f:[a,b]\to\mathbb{R}$](/tex-image/07e4152f2a4d597fc3abcb3ab22d8459.png) continua en continua en ![TEX: $[a,b]$](/tex-image/053b830c701e1c282c7c235b9caf96bc.png) y dos veces derivable en y dos veces derivable en 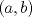 y sea y sea 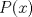 un polinomio de grado 1 (recta). Si un polinomio de grado 1 (recta). Si 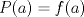 y y 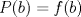 , se pide probar que para cada , se pide probar que para cada 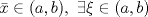 tal que: tal que:![TEX: \[f(\bar{x})=P(\bar{x})+\frac{f^{\prime\prime} (\xi)}{2} (\bar{x}-a)(\bar{x}-b)\]](/tex-image/e0b22bf6608a5ccbb34d2482a26df8b8.png) Para esto proceda como sigue Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Nov 9 2013, 06:47 PM -------------------- |
|
|
|
 Nov 5 2013, 06:53 AM Nov 5 2013, 06:53 AM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 10-1 Control 1 Semestre Otoño 2010
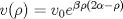 , ajusta adecuadamente la velocidad , ajusta adecuadamente la velocidad 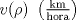 del tránsito en una carretera, en función de la densidad del tráfico del tránsito en una carretera, en función de la densidad del tráfico 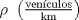 , en que , en que 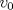 es la "velocidad libre" y es la "velocidad libre" y  y y 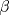 parámetros característicos de la carretera. parámetros característicos de la carretera.
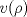 alcanza su máximo cuando la densidad de tránsito es alcanza su máximo cuando la densidad de tránsito es 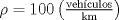 y vale y vale 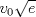 , se pide determinar , se pide determinar  y y 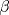 . .b) (2,0 ptos.) Determine el valor de 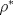 que maximiza la función que maximiza la función 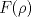 de flujo vehicular en la carretera definida por de flujo vehicular en la carretera definida por 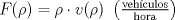 - Pruebe que - Pruebe que 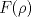 es creciente para es creciente para 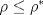 y decreciente para y decreciente para 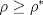 . .c) (2,0 ptos.) Si por razones reglamentarias se impone que la velocidad 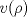 no supere no supere 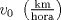 , determine el rango de variación de la variable , determine el rango de variación de la variable 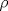 que respecta dicha restricción y en este caso encuentre el nuevo máximo globo de la función que respecta dicha restricción y en este caso encuentre el nuevo máximo globo de la función 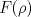 . Justifique. . Justifique.
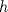 , derivable en , derivable en 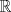 , satisface que , satisface que 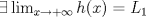 y y 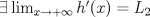 , entonces, necesariamente, , entonces, necesariamente, 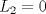 . .b) Sean 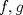 funciones derivables en funciones derivables en 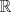 tales que tales que 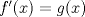 y y 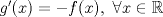 . .
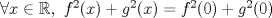 . .Indicación: Aplique el TVM a la función auxiliar 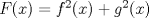 . .b2) Demuestre que no es posible que 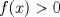 y y 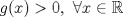 . Para ello, suponga por contradicción, que . Para ello, suponga por contradicción, que 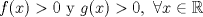 y con ello estudie. y con ello estudie.
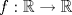 definida por: definida por:![TEX: \[f(x)=\begin{cases}<br />x\sin x \sin \frac{1}{x} &\text{, si } x\neq 0\\<br />\alpha & \text{, si } x=0<br />\end{cases}\]](/tex-image/e41887eb528465e50191daea7655a516.png) ![TEX: $f,g: [a,b]\to [c,d]$](/tex-image/f1ce0416dce872410cc8dd505ce0c481.png) continuas en continuas en ![TEX: $[a,b]$](/tex-image/7d78eee13f2ef4e5f580b23179a581ac.png) y tales que y tales que 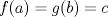 . Demuestre que . Demuestre que ![TEX: $\exists x_0 \in [a,b]$](/tex-image/8ec923d92dd85ac77efcf4071d7a229e.png) , tal que , tal que 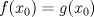 . .Tiempo: 3 horas Soluciones: P1. P2. P3. -------------------- |
|
|
|
 Nov 5 2013, 06:55 AM Nov 5 2013, 06:55 AM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente.
-------------------- |
|
|
|
 Nov 5 2013, 06:56 AM Nov 5 2013, 06:56 AM
Publicado:
#9
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente.
-------------------- |
|
|
|
 Nov 5 2013, 06:58 AM Nov 5 2013, 06:58 AM
Publicado:
#10
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Cálculo Diferencial 11-2 Control 1 Semestre Primavera 2011
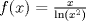 . Se pide: . Se pide:
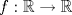 definida por definida por 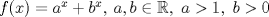 . .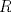 , se desea construir un cono, recortando del círculo el sector circular , se desea construir un cono, recortando del círculo el sector circular 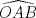 del ángulo central del ángulo central  y juntando los trazos y juntando los trazos 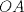 y y 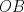 de modo que coincidan. Se formará de esta manera un cono recto circular cuya base es un círculo de perímetro igual a la longitud del arco que queda después del corte, y su altura de modo que coincidan. Se formará de esta manera un cono recto circular cuya base es un círculo de perímetro igual a la longitud del arco que queda después del corte, y su altura 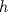 puede deducirse del esquema que se muestra. puede deducirse del esquema que se muestra.Figura: Para calcular el valor del ángulo  de modo que el cono formado como se indicó tenga volumen máximo, se pide: de modo que el cono formado como se indicó tenga volumen máximo, se pide:Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el May 17 2014, 02:39 PM -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 04:18 AM |





![TEX: \[\forall u,v \in \mathbb{R}^n, (u\cdot v)^2\leq\|u\|^2\|v\|^2\]](/tex-image/283098445a030208c5fa871145b851c6.png) Cauchy y Schwarz... Y Bun...
Cauchy y Schwarz... Y Bun...
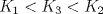 ???[/juice]
???[/juice]


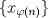 converge a
converge a 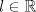 , entonces
, entonces  .
.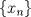 tiene alguna subsucesión que converge a
tiene alguna subsucesión que converge a 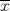 .
.
![TEX: $x_0 \in [0,1]$](/tex-image/9c0ba3f1ae68c5415376aa5352a56cac.png) tal que
tal que 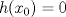 .
.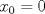 es un punto de inflexión de
es un punto de inflexión de 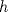 .
.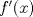 y determine irrtervalos de crecimiento, máximos y mínimos.
y determine irrtervalos de crecimiento, máximos y mínimos. 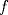 en su dominio se encuentra en
en su dominio se encuentra en ![TEX: $[-2,-1]$](/tex-image/f850d6e1d501c4260fac97ebe27c4f1d.png) .
. 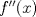 y determine convexidades y puntos de inflexión si los hay.
y determine convexidades y puntos de inflexión si los hay. 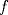 e indique recorrido de
e indique recorrido de 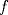 .
. 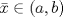 , justifique que existe un único
, justifique que existe un único 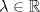 para el cual la función
para el cual la función 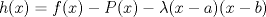 se anula en
se anula en 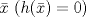 .
. 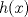 en
en ![TEX: $[a,\bar{x}]$](/tex-image/96fd65aa9c52af16e2ab3caad9d49b1e.png) y en
y en ![TEX: $[\bar{x},b]$](/tex-image/227a748998d7f0aa749c66e1576de2bf.png) justificando sus hipótesis.
justificando sus hipótesis. 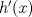 para probar que
para probar que 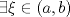 tal que
tal que 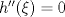 .
. 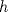 para calcular el valor de
para calcular el valor de 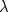 en función de
en función de 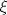 y ocupe este resultado y el del punto (i). Concluya.
y ocupe este resultado y el del punto (i). Concluya. ![TEX: $f: [0,1]\to\mathbb{R}$](/tex-image/c4afa30adab92bc65b0f4f05556eb583.png) continua en
continua en ![TEX: $[0,1]$](/tex-image/fde33b242251ca0980886fbd7d4257e5.png) con
con 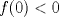 y
y 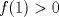 .
. 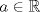 se define
se define ![TEX: $g:[0,1]\to \mathbb{R}$](/tex-image/ed4718985f7dab2dcf84201261c5324d.png) por
por 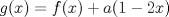 . Encuentre todos los valores de
. Encuentre todos los valores de 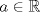 que garanticen que la función
que garanticen que la función 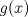 tendrá al menos un cero en
tendrá al menos un cero en ![TEX: $[0,1]$](/tex-image/c6aa0aed8099cfe9e5db1af9c0584ed9.png) .
.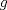 y
y 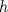 funciones definidas en
funciones definidas en ![TEX: $[-a,a]$](/tex-image/e94825b38a893577d7edba1e3521aa99.png) tales que
tales que 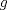 es derivable en
es derivable en 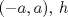 es tres veces derivable en
es tres veces derivable en 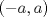 y
y![TEX: \[h(0)=h^\prime (0)=0,\, g(0)\neq 0, h^{\prime\prime} (0) \neq 0\]](/tex-image/3d5218e4a6fc180217c5764ead055467.png)
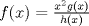 , calcule
, calcule 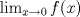 .
. 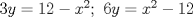
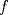 y
y 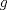 .
.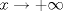 de
de 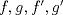 .
.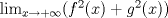 .
.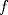 para
para 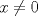 y determine el valor de
y determine el valor de  para la continuidad de
para la continuidad de 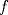 en
en 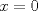 .
.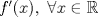 .
.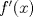 en
en 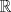 .
.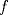 .
.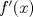 para
para 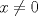 y, si es posible,
y, si es posible, 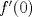 . Analice crecimientos. Encuentre máximos y mínimos.
. Analice crecimientos. Encuentre máximos y mínimos.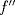 . Estudie concavidad, convexidad e inflexiones.
. Estudie concavidad, convexidad e inflexiones.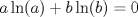 , entonces,
, entonces, 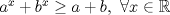 , es decir
, es decir 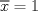 es punto de mínimo global de
es punto de mínimo global de 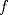 . Para esto proceda como sigue:
. Para esto proceda como sigue: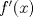 , demuestre, usando la propiedad, que puede escribirse como
, demuestre, usando la propiedad, que puede escribirse como![TEX: \[f^\prime (x)=a^x\ln (a)\left[1-\left(\frac{b}{a}\right)^{x-1}\right]\]](/tex-image/937240231fdacaf0a61afe7fec77d060.png)
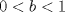 . Calcule
. Calcule 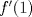 . Estudie crecimientos de
. Estudie crecimientos de 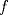 . Concluya.
. Concluya.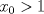 tal que
tal que 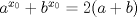 .
.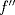 existe
existe 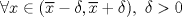 y
y 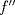 es continua en
es continua en 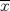 , entonces
, entonces![TEX: \[\lim_{h\to 0}\frac{f(\overline{x}+h)-2f(\overline{x})+f(\overline{x}-h)}{h^2}=f^{\prime\prime}(x)\]](/tex-image/b982b25aad69c373a5e0e841fbb084a6.png)
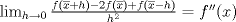 incluso existe si
incluso existe si 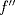 existe solamente en
existe solamente en 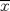 .
. del cono es
del cono es 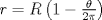 .
.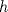 del cono es
del cono es 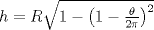 .
.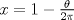 el volumen del cono queda
el volumen del cono queda![TEX: \[V(x)=\frac{1}{3}R^3x^2\sqrt{1-x^2}\]](/tex-image/7accf859aa81b54d151937337a458257.png)
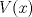 indicando: dominio, ceros, signos de
indicando: dominio, ceros, signos de 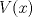 , la paridad, cálculo de
, la paridad, cálculo de 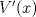 , crecimientos y deduzca el valor de
, crecimientos y deduzca el valor de  que hace máximo a
que hace máximo a 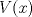 .
. que lo genera.
que lo genera.