|
|
|
|
|
|
|
  |
 Oct 26 2013, 06:11 PM Oct 26 2013, 06:11 PM
Publicado:
#1
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Voy a empezar a poner todos los controles 1 de Álgebra Lineal en este tema (y en general voy a empezar a hacer lo mismo para todos los controles para todos los ramos de primer año… quizá lo haga para ramos de semestres posteriores si logro encontrarlos). La idea principal de esto es dejar un tema en que estén todos los controles y que siga creciendo con el tiempo, por lo que se ruega a los usuarios NO POSTEAR. Cualquier corrección de enunciado, comentario o soluciones que quieran aportar, por favor mandarlas por MP. Este aporte va a ser mejor en tanto que ustedes también aporten con soluciones y con algunas pruebas que faltan. Sin más que decir, partamos
Dudas, preguntas, aclaraciones, sugerencias por MP. Mensaje modificado por TribalJazz2 el Oct 17 2014, 10:26 AM -------------------- |
|
|
|
 Oct 26 2013, 06:12 PM Oct 26 2013, 06:12 PM
Publicado:
#2
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 07-2 Control 1 Semestre Primavera 2007
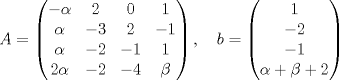
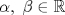 para los cuales el sistema Ax=b, con para los cuales el sistema Ax=b, con 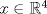 , ,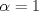 y y 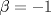 , encuentre la inversa de la matriz A y la solución del sistema Ax=b propuesto. , encuentre la inversa de la matriz A y la solución del sistema Ax=b propuesto. el plano de ecuación cartesiana el plano de ecuación cartesiana  . .
 . .b) (1,0 pto.) Encuentre una ecuación vectorial de la recta L que pasa por P y es ortogonal a  . Pruebe que L pasa por el origen. . Pruebe que L pasa por el origen.c) (2,0 ptos.) Encuentre una ecuación cartesiana para el plano que contiene a L y al eje 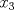 (es decir, al eje (es decir, al eje 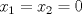 ). ).d) (2,0 ptos.) Encuentre una ecuación cartesiana del plano equidistante de  y P. y P.
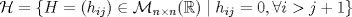 . .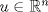 con con 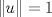 . Demostrar que la matriz . Demostrar que la matriz![TEX: \[A=I-2uu^T,\]](/tex-image/7a2a555cf9bca28c4ce628b9bc6a8739.png) es invertible, con A-1=A. Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 21 2014, 11:26 AM -------------------- |
|
|
|
 Oct 26 2013, 06:15 PM Oct 26 2013, 06:15 PM
Publicado:
#3
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 08-1 Control 1 Semestre Otoño 2008
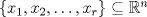 es un conjunto ortogonal si para todo par de indices es un conjunto ortogonal si para todo par de indices 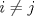 , se tiene que , se tiene que 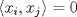 . Sea . Sea 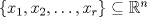 un conjunto ortogonal tal que para todo un conjunto ortogonal tal que para todo 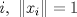 . .
![TEX: \[\begin{pmatrix}<br />1&0&3\\<br />0&3&2\\<br />1&-9&-1<br />\end{pmatrix}\]](/tex-image/f4ad12c1d4c39a1bcd214ebdcc7af7fa.png) b) (4,0 ptos.) Sea el sistema: 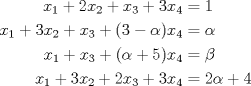 Encontrar los valores de  y y 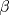 tal que: tal que: el plano que pasa por el origen y tiene directores d1=(-1,2,1), (1,-1,0). el plano que pasa por el origen y tiene directores d1=(-1,2,1), (1,-1,0).Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 21 2014, 11:28 AM -------------------- |
|
|
|
 Oct 26 2013, 06:19 PM Oct 26 2013, 06:19 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 08-2 Control 1 Semestre Primavera 2008
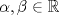 , Ax=b donde , Ax=b donde![TEX: \[A=\begin{pmatrix}<br />2 & 1 & 1-2\alpha & \beta+1\\<br />0 & 1 & -1 & \beta-\alpha\\<br />0 & -2 & 2 & 2-2\beta\\<br />2 & 0 & 2 & \alpha\\<br />2 & 1 & 1 & \alpha +\beta -1<br />\end{pmatrix},\quad<br />b=\begin{pmatrix}<br />\beta-3\\<br />-1\\<br />-2\\<br />4\beta-3\\<br />0<br />\end{pmatrix}\]](/tex-image/5e0d9a74465f6a89aeee337a92fc11be.png) Determine los valores o condiciones para los parámetros  y y 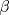 de modo que el sistema: de modo que el sistema:![TEX: \[<br />L_1\begin{cases}<br />x+z=1\\<br />\alpha x+y+z=0<br />\end{cases}\quad<br />L_2\begin{cases}<br />2\alpha x +y+z=1\\<br />x+y+z+2=0<br />\end{cases}\quad \alpha\in\mathbb{R}\]](/tex-image/69b588031bf5bc277614911347a07726.png)
![TEX: \[\Pi :x+y+z=1\]](/tex-image/260077fbb41d274d7ac1d6982cb446a1.png) Determine las coordenadas del punto proyección del origen sobre el plano  y calcule la distancia del origen al plano y calcule la distancia del origen al plano  . .
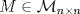 se llama Idempotente si M2=M. Si se llama Idempotente si M2=M. Si 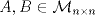 son tales que A=AB y B=BA demuestre que A y B son idempotentes. son tales que A=AB y B=BA demuestre que A y B son idempotentes.b) Sea 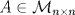 dada y supongamos que A3=0. Considere el conjunto de matrices dada y supongamos que A3=0. Considere el conjunto de matrices ![TEX: \[G=\{M(\lambda)\in\mathcal{M}_{n\times n} \mid \lambda\in\mathbb{R}\}\]](/tex-image/cbda94754af36fdd56186ec7f3196537.png) ![TEX: \[M(\lambda)=I+\lambda A+\frac{\lambda^2}{2} A^2\]](/tex-image/b7bbe9dd6e63a4433df7c8db2365c668.png)
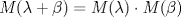 . .b.2) (2,0 ptos.) Demuestre que 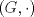 es un grupo abeliano, donde . es el producto de matrices. Identifique es un grupo abeliano, donde . es el producto de matrices. Identifique  . .Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 18 2014, 06:42 PM -------------------- |
|
|
|
 Oct 26 2013, 06:32 PM Oct 26 2013, 06:32 PM
Publicado:
#5
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 09-1 Control 1 Semestre Otoño 2009
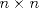 tal que KT=-K e I-K es invertible. Si B=(I+K)(I-K)-1, demuestre que BTB=BBT=In. tal que KT=-K e I-K es invertible. Si B=(I+K)(I-K)-1, demuestre que BTB=BBT=In.Indicación: Compruebe primero que (I+K)T=(I-K) y (I+K)(I-K)=(I-K)(I+K). b) Sean  y y  dos vectores no nulos y no paralelos en dos vectores no nulos y no paralelos en 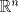 . Demuestre que . Demuestre que 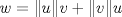 es un vector no nulo que bisecta el ángulo entre es un vector no nulo que bisecta el ángulo entre  y y  . .c) Sean  y y  dos vectores no nulos y no paralelos en dos vectores no nulos y no paralelos en 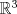 . Demuestre que los vectores . Demuestre que los vectores  , , 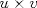 y y 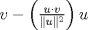 son ortogonales de a pares. son ortogonales de a pares.d) Sea Ax=b un sistema de ecuaciones lineales y 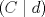 su forma escalonada. Discuta las afirmaciones: su forma escalonada. Discuta las afirmaciones:
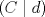 tiene una fila nula. tiene una fila nula.El sistema tiene más de una solución si y sólo si 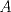 tiene una fila nula. tiene una fila nula.
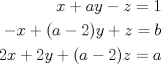  y y  para los cuales el sistema para los cuales el sistema
(ii) tenga una única solución (iii) tenga infinitas soluciones 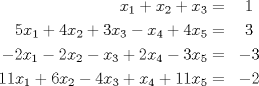 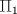 el plano que pasa por p1 y tiene direcciones d' y d'' y el plano que pasa por p1 y tiene direcciones d' y d'' y 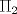 el plano definido por el plano definido por 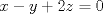 . .Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jun 30 2014, 12:02 PM -------------------- |
|
|
|
 Oct 26 2013, 07:16 PM Oct 26 2013, 07:16 PM
Publicado:
#6
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 09-2 Control 1 Semestre Primavera 2009
![TEX: \[<br />\begin{matrix}<br />x_1 & -\alpha\cdot x_2 & +0\cdot x_3 & -\beta \cdot x_4 = 0\\<br />0\cdot x_1 & +\alpha\cdot x_2 & +x_3 & +\beta \cdot x_4 = \alpha\\<br />\beta\cdot x_1 & +\alpha\cdot x_2 & +\beta\cdot x_3 & +0 \cdot x_4 = \beta\\<br />\alpha\cdot x_1 & 0 \cdot x_2 & +\beta \cdot x_3 & 0 \cdot x_4 = 0<br />\end{matrix}<br />\]](/tex-image/b3d917e236b7ba59deab7f6765874054.png) donde 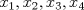 son las incógnitas y son las incógnitas y 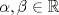 son parámetros. son parámetros.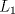 y y 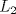 definidas por definidas por![TEX: \[L_1: \begin{pmatrix}<br />0\\<br />1\\<br />0<br />\end{pmatrix}+t\begin{pmatrix} 1\\1\\1 \end{pmatrix},\ t\in\mathbb{R}\text{ \ \ y \ \ } L_2:\begin{cases} x-z-1=0\\y+z-2=0\end{cases}\]](/tex-image/62d88376fba9d1e977a1b99effb026ba.png) se pide: b) (2,0 ptos.) Sea P3. Sean 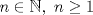 y y 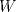 definido por definido por![TEX: \[W=\{A\in\mathcal{M}_{n\times n}(\mathbb{R})\mid A\text{ es sim\'etrica y }\sum_{i=0}^{n} a_{ii}=0\}\]](/tex-image/838ae491105ec8ed511ebcf8aa594b97.png)
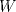 es s.e.v. de es s.e.v. de 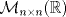 . .b) Considere 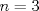 y las matrices de y las matrices de 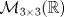 ![TEX: \[A=\begin{pmatrix}0&1&0\\<br />1&0&0\\<br />0&0&0<br />\end{pmatrix}\ B=\begin{pmatrix}<br />0 & 0 & 1\\<br />0 & 0 & 0\\<br />1 & 0 & 0<br />\end{pmatrix}\ C=\begin{pmatrix}<br />0 &0 & 0\\<br />0 & 0 & 1\\<br />0 & 1 & 0<br />\end{pmatrix}\ D=\begin{pmatrix}<br />1 & 0 & 0\\<br />0 & 0 & 0\\<br />0 & 0 & -1<br />\end{pmatrix}\ E=\begin{pmatrix}<br />0 & 0 & 0\\<br />0 & 1 & 0\\<br />0 & 0 & -1<br />\end{pmatrix}\]](/tex-image/e9c20c0f03063f13f6b48602c555f4f5.png)
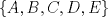 es l.i. es l.i.b.2) (2,0 ptos.) Pruebe que 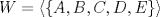 Tiempo: 3 horas Soluciones: P1. P2. P3. Mensaje modificado por TribalJazz2 el Jul 21 2014, 11:30 AM -------------------- |
|
|
|
 Oct 26 2013, 07:17 PM Oct 26 2013, 07:17 PM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente. (Se agradecen aportes.)
Mensaje modificado por TribalJazz2 el Oct 27 2013, 03:50 PM -------------------- |
|
|
|
 Oct 26 2013, 07:17 PM Oct 26 2013, 07:17 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente. (Se agradecen aportes.)
Mensaje modificado por TribalJazz2 el Oct 27 2013, 03:50 PM -------------------- |
|
|
|
 Oct 26 2013, 07:18 PM Oct 26 2013, 07:18 PM
Publicado:
#9
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Pendiente. (Se agradecen aportes.)
Mensaje modificado por TribalJazz2 el Oct 27 2013, 03:51 PM -------------------- |
|
|
|
 Oct 26 2013, 07:23 PM Oct 26 2013, 07:23 PM
Publicado:
#10
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 26-December 10 Desde: Nuncajamás. Miembro Nº: 82.286 Nacionalidad:  Sexo:  |
Ingeniería Matemática Facultad de Ciencias Físicas y Matemáticas Álgebra Lineal 11-2 Control 1 Semestre Primavera 2011
![TEX: \[\begin{matrix}<br />-x_1 & & +\alpha x_3 & +\beta x_4 = 0\\<br /> & x_2 & +\alpha x_3 & +\beta x_4 = 0\\<br />\alpha x_1 & +\beta x_2 & & =0\\<br />\beta x_1 & +\beta x_2 & +\alpha x_3 & =0<br />\end{matrix}\]](/tex-image/364ebc9289cd4394113e81bc165f31e0.png)  y y 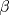 que garanticen que el sistema tenga una única solución. que garanticen que el sistema tenga una única solución.(b) (3,0 ptos.) Sea 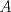 la matriz de coeficientes reales definida por: la matriz de coeficientes reales definida por:![TEX: \[A=\begin{pmatrix}<br />1 & 1 & 1\\<br />a & b & c\\<br />a^2 & b^2 & c^2<br />\end{pmatrix}\]](/tex-image/d8daecd24a88a5b51c4870d1c7a11c75.png) 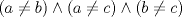 . .Tiempo: 2,25 horas Soluciones: P1. P2. Mensaje modificado por TribalJazz2 el Jul 18 2014, 07:04 PM -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 08:46 PM |





![TEX: \[\forall u,v \in \mathbb{R}^n, (u\cdot v)^2\leq\|u\|^2\|v\|^2\]](/tex-image/283098445a030208c5fa871145b851c6.png) Cauchy y Schwarz... Y Bun...
Cauchy y Schwarz... Y Bun...
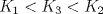 ???[/juice]
???[/juice]


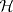 es subespacio vectorial de
es subespacio vectorial de 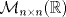 .
.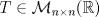 es triangular superior, y
es triangular superior, y 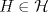 , entonces
, entonces 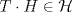 .
.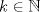 , Pk=P.
, Pk=P.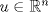 tal que
tal que 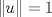 , entonces P=uuT cumple que Pk=P.
, entonces P=uuT cumple que Pk=P.![TEX: \[x_{r+1}=y-\sum_{k=1}^{r} \langle y, x_k\rangle x_k\]](/tex-image/3dcf1b24a5401f7ddbe01ebf44c3210e.png)
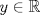 . Pruebe que
. Pruebe que 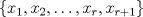 es un conjunto ortogonal.
es un conjunto ortogonal.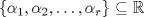 tal que
tal que 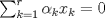 , entonces
, entonces 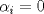 para todo
para todo 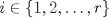 .
.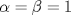 .
.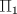 .
.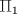 con el plano
con el plano 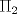 de ecuación
de ecuación 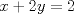 .
. los conjuntos L1 y L2
los conjuntos L1 y L2 para que L1 y L2 sean ortogonales y, para ese valor de
para que L1 y L2 sean ortogonales y, para ese valor de  , verifique que
, verifique que 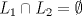 .
.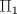 y
y 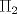 .
.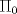 que pasa por p1 y es ortogonal a L.
que pasa por p1 y es ortogonal a L.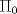 ,
, 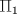 ,
, 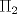 está más cerca de p0, usando:
está más cerca de p0, usando: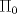 ,
,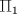 ,
,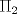 .
. y
y 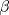 de modo que el sistema:
de modo que el sistema: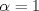 y
y 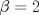 , encuentre, de ser posible, la solución del sistema.
, encuentre, de ser posible, la solución del sistema.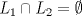 .
.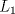 y es paralelo a
y es paralelo a 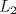 .
.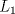 y
y 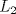 .
.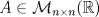 y
y 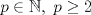 . Pruebe que
. Pruebe que 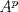 es invertible si y sólo si
es invertible si y sólo si 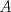 es invertible.
es invertible.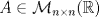 invertible tal que satisface la condición
invertible tal que satisface la condición ![TEX: \[A\cdot (A^2 +3A+I)=0\]](/tex-image/2cc5042181a30df05f9bd147de09b18e.png)
 .
.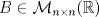 invertible y tal que satisface
invertible y tal que satisface 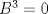 . Para cada
. Para cada 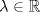 se define
se define 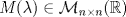 por
por ![TEX: \[M(\lambda)=I+\lambda B+\frac{\lambda^2}{2}B^2\]](/tex-image/0cffc96c2ec587195a55225bf9a49c43.png)
![TEX: \[\forall \lambda, \beta\in\mathbb{R},\quad M(\lambda+\beta)=M(\lambda) \cdot M(\beta)\]](/tex-image/a8f253018c328f5fb5cc3e4761cf5596.png)
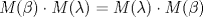
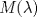 es invertible y que
es invertible y que 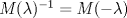 .
.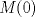 .
.