I1 Teoría de la Integración - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Teoría de la Integración

Reply to this topic

Start new topic

I1 Teoría de la Integración, 2013 2S

Cenizas con Most... Cenizas con Mostaza Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2013, 07:53 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad: Universidad: Sexo:	$TEX: \begin{center}<br /> \textbf{Interrogación 1 Teoría de la Integración}<br /> \end{center}<br /> \begin{flushright}<br /> Santiago, 26 de septiembre de 2013<br /> <br /> Profesor: Gregorio Moreno.<br /> <br /> \end{flushright}<br /><br /> \begin{enumerate}<br /> \item[\textbf{P1}] Sea $\mu$ la medida de Lebesgue sobre $\mathbb{R}$. Considere $E\subseteq \mathbb{R}$ medible con $\mu(E)<+\infty$ y $f:E\to [0,+\infty]$ una función medible finita $\mu$-c.t.p. Demuestre que $\forall \epsilon>0$, existe un conjunto medible $A\subseteq E$ tal que $\mu(E\setminus A)<\epsilon$ y tal que $f\|_A$ es acotada. \end{enumerate}$ $TEX: \begin{enumerate}<br /> \item[\textbf{P2.}] Sea $f:[a,b]\to \mathbb{R}$ continua y sea $F:[a,b]\to \mathbb{R}$ tal que $$F(x)=\displaystyle \int_{a}^{x} f(t)dt,\forall x\in [a,b]$$ (donde la integral es la integral de Riemann). <br /><br /> \begin{enumerate} \item[(2.1)] Pruebe que $F$ es continua en $[a,b]$<br /> \item[(2.2)] Pruebe que $F$ es diferenciable en $(a,b)$ y determine su derivada. <br /> \end{enumerate}<br /><br /> \end{enumerate}$ $TEX: \begin{enumerate}<br />\item[\textbf{P3.}] Sea $(\Omega,\mathcal{F})$ un espacio medible y $f:\Omega\to \mathbb{R}$<br /><br /> \begin{enumerate}<br /> \item[(3.1)] Pruebe que si $f$ es medible, entonces $\|f\|$ es medible. <br /> \item[(3.2)] Construya un ejemplo de una función $f$ no medible tal que $\|f\|$ es medible.<br /> \item[(3.3)] Suponga que $\Omega=(0,1)$, $\mathcal{F}$ es la completación de los borelianos de $(0,1)$ y que $\mu$ es la medida de Lebesgue definida sobre $(\Omega,\mathcal{F})$. Suponga que $\mathcal{F}$ es diferenciable $\mu$-c.t.p. Pruebe que $f'$ es medible. <br /> <br /> \end{enumerate} <br /> \end{enumerate}$ $TEX: \begin{enumerate}<br /> \item[\textbf{P4.}] Sea $\mathcal{C}=\{[a,b):a,b\in \mathbb{R},a\leq b\}$, $\tau:\mathcal{C}\to [0,+\infty]$ la premedida tal que $\tau([a,b))=b-a$ si $a<b$ y $\tau(\emptyset)=0$, y sea $\mu^$ la medida exterior asociada a $\tau$. Sea $c\in \mathbb{R}$ y sean $A,B$ subconjuntos de $\mathbb{R}$ tales que $A\subseteq (-\infty,c)$ y $B\subseteq (c,+\infty)$. Demuestre que $\mu^(A\cup B)=\mu^(A)+\mu^(B)$<br /><br /> \end{enumerate}$ Tiempo: 150 minutos. Sí, esta fue la prueba. -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass!

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2013, 09:12 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	Gregorio? Ah no disfruta el curso! -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 5 2013, 07:57 PM Publicado: #3
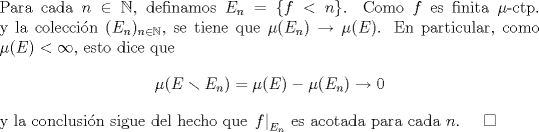
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P1 $TEX: \noindent Para cada $n\in\mathbb N$, definamos $E_n=\{f<n\}$. Como $f$ es finita $\mu$-ctp. y la colección $(E_n)_{n\in\mathbb N}$, se tiene que $\mu(E_n)\to\mu(E)$. En particular, como $\mu(E)<\infty$, esto dice que<br />$$\mu(E\smallsetminus E_n)=\mu(E)-\mu(E_n)\to 0$$<br />y la conclusión sigue del hecho que $\left.f\right\|_{E_n}$ es acotada para cada $n$. $\quad\square$<br />$ Mensaje modificado por Abu-Khalil el Oct 5 2013, 07:58 PM -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 5 2013, 10:36 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kaissa @ Sep 28 2013, 09:12 PM) Gregorio? Ah no disfruta el curso! Es muy conocido ese profesor? Él me hizo cálculo lll y fue excelente, además sé que en su tiempo su profesor guía en su tesis fue Alejandro Ramirez, otro excelente profesor que no hizo sudar en EDO. -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

febomon Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 5 2013, 11:13 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad: Sexo:	Junto a duvan son las maquinas de la facultad. Cuenta la leyenda que siendo muy chicos ayudaban a los profes en sus investigaciones

MysticMan Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 5 2013, 11:18 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 550 Registrado: 24-July 11 Desde: Chillán Miembro Nº: 92.177 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(febomon @ Oct 6 2013, 12:13 AM) Junto a duvan son las maquinas de la facultad. Cuenta la leyenda que siendo muy chicos ayudaban a los profes en sus investigaciones Duvan <3. -------------------- $TEX: $$1782^{12}+1841^{12}=1922^{12}$$$

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 5 2013, 11:25 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(febomon @ Oct 5 2013, 11:13 PM) Junto a duvan son las maquinas de la facultad. Cuenta la leyenda que siendo muy chicos ayudaban a los profes en sus investigaciones Existen leyendas que son conocidas por agrandar hechos... otras son más normales... y hay otras que parece que agrandan hechos pero no. Esta es una. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

CnstMot Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 5 2013, 11:51 PM Publicado: #8
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 182 Registrado: 18-February 13 Desde: Santiago Miembro Nº: 115.462 Nacionalidad: Universidad: Sexo:	CITA(MysticMan @ Oct 5 2013, 11:18 PM) Duvan <3. Duvancito <333 -------------------- Standing above the crowd, He had a voice that was strong and loud and I Swallowed his facade cuz I'm so Eager to identify with Someone above the ground, Someone who seemed to feel the same, Someone prepared to lead the way, and Someone who would die for me. Will you? Will you now? Would you die for me?

aleabrahamramire... aleabrahamramirez Ver Perfil del Miembro Ver los mensajes de este miembro	May 17 2016, 09:18 PM Publicado: #9
Dios Matemático Grupo: Usuario FMAT Mensajes: 206 Registrado: 25-January 11 Miembro Nº: 83.389	CITA(Cenizas con Mostaza @ Sep 28 2013, 08:53 PM) $TEX: \begin{center}<br /> \textbf{Interrogación 1 Teoría de la Integración}<br /> \end{center}<br /> \begin{flushright}<br /> Santiago, 26 de septiembre de 2013<br /> <br /> Profesor: Gregorio Moreno.<br /> <br /> \end{flushright}<br /><br /> \begin{enumerate}<br /> \item[\textbf{P1}] Sea $\mu$ la medida de Lebesgue sobre $\mathbb{R}$. Considere $E\subseteq \mathbb{R}$ medible con $\mu(E)<+\infty$ y $f:E\to [0,+\infty]$ una función medible finita $\mu$-c.t.p. Demuestre que $\forall \epsilon>0$, existe un conjunto medible $A\subseteq E$ tal que $\mu(E\setminus A)<\epsilon$ y tal que $f\|_A$ es acotada. \end{enumerate}$ $TEX: \begin{enumerate}<br /> \item[\textbf{P2.}] Sea $f:[a,b]\to \mathbb{R}$ continua y sea $F:[a,b]\to \mathbb{R}$ tal que $$F(x)=\displaystyle \int_{a}^{x} f(t)dt,\forall x\in [a,b]$$ (donde la integral es la integral de Riemann). <br /><br /> \begin{enumerate} \item[(2.1)] Pruebe que $F$ es continua en $[a,b]$<br /> \item[(2.2)] Pruebe que $F$ es diferenciable en $(a,b)$ y determine su derivada. <br /> \end{enumerate}<br /><br /> \end{enumerate}$ $TEX: \begin{enumerate}<br />\item[\textbf{P3.}] Sea $(\Omega,\mathcal{F})$ un espacio medible y $f:\Omega\to \mathbb{R}$<br /><br /> \begin{enumerate}<br /> \item[(3.1)] Pruebe que si $f$ es medible, entonces $\|f\|$ es medible. <br /> \item[(3.2)] Construya un ejemplo de una función $f$ no medible tal que $\|f\|$ es medible.<br /> \item[(3.3)] Suponga que $\Omega=(0,1)$, $\mathcal{F}$ es la completación de los borelianos de $(0,1)$ y que $\mu$ es la medida de Lebesgue definida sobre $(\Omega,\mathcal{F})$. Suponga que $\mathcal{F}$ es diferenciable $\mu$-c.t.p. Pruebe que $f'$ es medible. <br /> <br /> \end{enumerate} <br /> \end{enumerate}$ $TEX: \begin{enumerate}<br /> \item[\textbf{P4.}] Sea $\mathcal{C}=\{[a,b):a,b\in \mathbb{R},a\leq b\}$, $\tau:\mathcal{C}\to [0,+\infty]$ la premedida tal que $\tau([a,b))=b-a$ si $a<b$ y $\tau(\emptyset)=0$, y sea $\mu^$ la medida exterior asociada a $\tau$. Sea $c\in \mathbb{R}$ y sean $A,B$ subconjuntos de $\mathbb{R}$ tales que $A\subseteq (-\infty,c)$ y $B\subseteq (c,+\infty)$. Demuestre que $\mu^(A\cup B)=\mu^(A)+\mu^(B)$<br /><br /> \end{enumerate}$ Tiempo: 150 minutos. Sí, esta fue la prueba. De por casualidad no tienes la I2, I3 y el examen (?)

« Posterior · Teoría de la Integración · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 05:29 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.