|
|
|
|
|
|
|
  |
 Sep 14 2013, 03:46 PM Sep 14 2013, 03:46 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
![TEX: \begin{center}<br /> \textbf{Interrogación Teoría de Números}<br /> \end{center}<br /> \begin{flushright}<br /> Santiago, 12 de septiembre de 2013<br /> <br /> Profesor: Kazim Buyükböduk<br /> <br /> \end{flushright}<br /><br /> \begin{enumerate}<br /> \item[\textbf{P1}] $\textbf{(17 pts)}$. Demuestre que la ecuación $15x^2-36=y^2$ no tiene solución en $\mathbb{Q}\times \mathbb{Q}$. \end{enumerate}](/tex-image/a38fb79676a6cf89ae4e6ce9f46bbf7e.png) ![TEX: \begin{enumerate}<br /> \item[\textbf{P2.}] $\textbf{(23 pts)}$ Encuentre un punto $(x_0,y_0)\in \{(x,y)\in \mathbb{Q}\times \mathbb{Q}:2x^2+y^2=6\}$, distinto de los puntos $(1,2),(-1,-2),(1,-2),(-1,-2)$.<br /> \end{enumerate}](/tex-image/c7b8895dc40b44f125c22f437504c99e.png) ![TEX: \begin{enumerate}<br />\item[\textbf{P3.}] $\textbf{(27 pts)}$ Encuentre todas las soluciones en $\mathbb{Z}^+\times \mathbb{Z}^+$ de la ecuación $x^2+2=y^3$. <br /> \end{enumerate}](/tex-image/c106fec4286ecb6d9cdb27b3f78a6ac1.png) ![TEX: \begin{enumerate}<br />\item[\textbf{Bonus}] $\textbf{(25 pts)}$ \begin{enumerate}<br />\item[\textbf{(1)}] Sea $p\ge 2$ un número primo, tal que $gcd(3,p-1)=1$. Demuestre que la ecuación $3x^3+4y^3+5z^3\equiv 0\pmod p$ tiene una solución módulo $p$ distinta de $(0,0,0)$.<br /><br />\item[\textbf{(2)}] Encuentre todos los enteros $0\leq n\leq 60$ tales que $n^3\equiv 1\pmod {61}$.<br /><br />\item[\textbf{(3)}] Demuestre que la ecuación $3x^3+4y^3+5z^3\equiv 0\pmod{61}$ tiene una solución módulo $61$ distinta de $(0,0,0)$. <br /> \end{enumerate}<br /> \end{enumerate}](/tex-image/a5df49b2f6ec6c5009e2d2c3f228871a.png) ![TEX: \begin{enumerate}<br />\item[\textbf{Tarea}] $\textbf{(33 pts)}$ \begin{enumerate}<br />\item[\textbf{(1)}] Sea $p>2$ un primo. Encuentre todos los pares $(x,y)\in \mathbb{Z}\times \mathbb{Z}$ tales que $x^2+1=y^p$. <br />\item[\textbf{(2)}] Note que $\epsilon=1+\sqrt{2}$ es unidad en $\mathbb{Z}[\sqrt{2}]$. Demuestre que el grupo de unidades positivas en $\mathbb{Z}[\sqrt{2}]$ es un grupo cíclico generado por $\epsilon$. Más aún, sea $N\in \mathbb{Z}$ libre de cuadrados. Demuestre que el grupo de unidades positivas de $\mathbb{Z}[\sqrt{N}]$ es isomorfo al grupo aditivo $\mathbb{Z}$. <br /> <br /> \end{enumerate}<br /> \end{enumerate}](/tex-image/a77ecb78fffa7918e953bccc82786b12.png) Tiempo parte presencial: 80 minutos.
Mensaje modificado por Cenizas con Mostaza el Sep 23 2013, 04:22 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Sep 23 2013, 12:27 AM Sep 23 2013, 12:27 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
P1. Suponga que existe tal solucion. Escriba
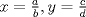 . Multiplique todo por . Multiplique todo por 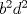 obteniendo obteniendo 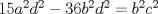 , escriba , escriba 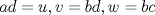 entonces la ecuacion se transforma en entonces la ecuacion se transforma en 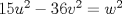 . Probemos que esta ultima ecuacion solo tiene . Probemos que esta ultima ecuacion solo tiene 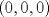 como solucion en los enteros. Suponga por el contrario que como solucion en los enteros. Suponga por el contrario que 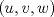 es una solucion distinto de es una solucion distinto de 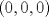 que tiene el que tiene el 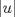 mas pequeño, se puede llegar facilmente a que mas pequeño, se puede llegar facilmente a que 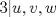 y por lo tanto y por lo tanto 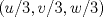 tambien es solucion contradiciendo el hecho que tambien es solucion contradiciendo el hecho que 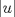 era el mas pequeño. De ahi concluimos que era el mas pequeño. De ahi concluimos que 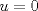 y luego que la unica solucion es y luego que la unica solucion es 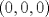 . Asi que tenemos que . Asi que tenemos que 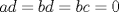 lo cual implica lo cual implica 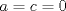 lo cual nos lleva a lo cual nos lleva a 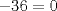 contradiccion. contradiccion.
Mensaje modificado por xD13G0x el Sep 23 2013, 12:28 AM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Sep 23 2013, 04:02 PM Sep 23 2013, 04:02 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
se puede llegar facilmente a que 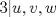 y por lo tanto y por lo tanto 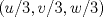 tambien es solucion contradiciendo el hecho que tambien es solucion contradiciendo el hecho que 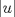 era el mas pequeño. era el mas pequeño.Esa era la parte difícil del problema. ¿Cómo lo justificas? EDIT: actualicé el enunciado de la I. Mensaje modificado por Cenizas con Mostaza el Sep 23 2013, 04:29 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Feb 25 2016, 12:46 AM Feb 25 2016, 12:46 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
BONUS.
(2). ![TEX: $n^{3} \equiv 1 \pmod{61}$ implica que $n\equiv 1 \pmod{61}$ o que $n^{2}+n+1\equiv 0 \pmod{61}$. De la primera congruencia se sigue que $n=1$. La segunda congruencia es equivalente a $(2n+1)^{2} \equiv -3 \pmod{61}$. Puesto que, en el intervalo $[0,60]$, una de las soluciones de la congruencia $x^{2}\equiv -3\pmod{61}$ es $x_{1}=27$, la segunda solución en ese mismo intervalo la da $x_{2}=61-27=34$. Por consiguiente, la única solución de la congruencia $(2n+1)^{2}\equiv-3 \pmod{61}$ (con $n\in [0,60]$) es $n=13.$ En conclusión, los números naturales $n \in [0,60]$ que satisfacen la congruencia original son $n=1$ y $n=13$.](/tex-image/3c0ee9b4571d81a26ba871da8a20f777.png) (3). 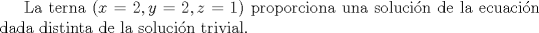
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Mar 2 2016, 10:43 PM Mar 2 2016, 10:43 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
P1.
 OBSERVACIÓN. Con 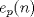 denoto ahí al exponente al cual aparece el primo denoto ahí al exponente al cual aparece el primo 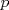 en la descomposición canónica de en la descomposición canónica de  . .
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 04:57 AM |










