 Consulta Inducción, demostración |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Álgebra > Inducción  |
  Jul 17 2013, 12:14 AM
Publicado:
#1
|
|
|
Principiante Matemático  Grupo: Usuario FMAT Mensajes: 13 Registrado: 24-May 13 Desde: Concepcion Miembro Nº: 119.077 Nacionalidad:  Universidad:  Sexo:   |
Ya demostré este ejercicio pero con pura lógica de desigualdades, pero quisiera saber si alguien puede hacer el procedimiento matemático y no teórico de esta demostración
 Muchas gracias por la ayuda |
 |
 
|
|
Jul 17 2013, 12:37 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 550 Registrado: 24-July 11 Desde: Chillán Miembro Nº: 92.177 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
¿Qué pasaría si
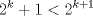 ?.Saludos. --------------------  |
|
|
|
|
Jul 17 2013, 12:52 AM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 13 Registrado: 24-May 13 Desde: Concepcion Miembro Nº: 119.077 Nacionalidad: Universidad: Sexo: |
CITA(MysticMan @ Jul 17 2013, 12:37 AM)  ¿Qué pasaría si ?.Saludos. Eso había planteado, es lo más evidente, pero quería saber si había otro procedimiento matemático  gracias mystic |
|
|
|
 Jul 17 2013, 05:24 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 11-April 10 Desde: Santiago Miembro Nº: 68.358 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
CITA quisiera saber si alguien puede hacer el procedimiento matemático y no teórico de esta demostración Las matemáticas son justamente teorías y sobretodo, mucha lógica. Si estabas buscando una "fórmula" para hacerlo, entonces te han lavado el cerebro respecto de lo que es hacer precisamente matemática. |
|
|
|
|
Jul 29 2013, 02:48 AM
Publicado:
#5
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 11-April 13 Miembro Nº: 117.372 Nacionalidad: Colegio/Liceo:  Sexo: |
podria hacerse asi? :
2(k+5)<2^(k)x2 = 2(k+5)<2^(k+1) (-k-4)+2k+10<2^(k+1) = k+6<2^(k+1) ; y el -k-4 siempre seria negativo porque k>=4 Mensaje modificado por nicooo-498 el Jul 29 2013, 02:57 AM |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:29 PM |
