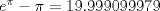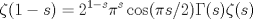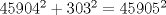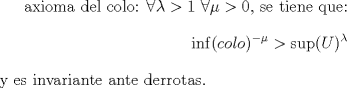|
|
|
|
|
|
|
  |
 Jun 10 2013, 08:43 PM Jun 10 2013, 08:43 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Bueno. este es mi post 500 asi que queria "celebrarlo" con un propuesto (a lo coquitao)
es bastante sencillo si se aplican bien algunas cosillas.  saludos Mensaje modificado por 2.718281828 el Sep 21 2014, 06:45 PM -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Sep 13 2014, 11:28 PM Sep 13 2014, 11:28 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
Bueno. este es mi post 500 asi que queria "celebrarlo" con un propuesto (a lo coquitao) es bastante sencillo si se aplican bien algunas cosillas.  saludos Hola! Si 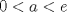 , la ecuación no tiene solución D: , la ecuación no tiene solución D:¿No será error de tipeo? ¿talvez quierías decir 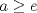 ? ?
Mensaje modificado por Laðeralus el Sep 13 2014, 11:32 PM |
|
|
|
 Sep 21 2014, 06:44 PM Sep 21 2014, 06:44 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Hola! Si 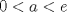 , la ecuación no tiene solución D: , la ecuación no tiene solución D:¿No será error de tipeo? ¿talvez quierías decir 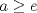 ? ?seguro que si. me confundo mucho con el geq y el leq. lo arreglo altiro. pd: no mefije que estaba saneado. Mensaje modificado por 2.718281828 el Sep 21 2014, 06:45 PM -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Jan 26 2024, 01:18 AM Jan 26 2024, 01:18 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
Se me había olvidado este propuesto de hace 11 años xd
Lo resolví pero seguramente buscabas otro método porque lo resolví sin la guía 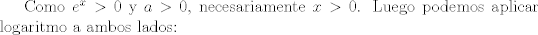 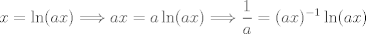 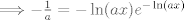 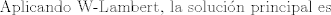 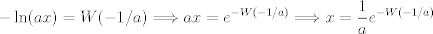 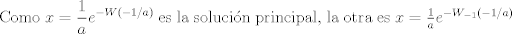 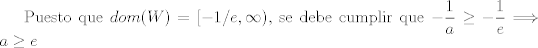 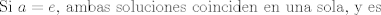 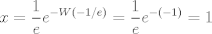 Saludos,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, Mensaje modificado por Laðeralus el Jan 26 2024, 07:36 AM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 17th April 2025 - 08:06 AM |