|
|
|
|
|
|
|
  |
 Apr 16 2013, 08:40 PM Apr 16 2013, 08:40 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 16-April 13 Miembro Nº: 117.697 |
Hola podrían ayudarme con esta demostracion
Sean 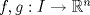 tal que tal que 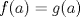 , donde , donde 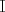 es un intervalo abierto y es un intervalo abierto y 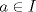 .Pruebe que .Pruebe que 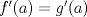 si,y sólo si, si,y sólo si,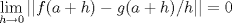
|
|
|
|
 Jun 18 2013, 08:28 PM Jun 18 2013, 08:28 PM
Publicado:
#2
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 31-March 12 Desde: Santiago de Chile Miembro Nº: 103.377 Nacionalidad:  Universidad:  Sexo:  |
Demostraremos un lado de la implicancia, como hipótesis tenemos que
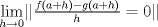 . .Usamos la continuidad de la norma para introducir el límite dentro; y además sumamos cero de una manera conveniente 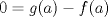 Con lo que nos quedaría: Con lo que nos quedaría: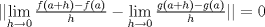 , pero por propiedades de la norma, la norma es cero si y solo si es la norma del vector cero, luego: , pero por propiedades de la norma, la norma es cero si y solo si es la norma del vector cero, luego: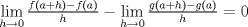 Y esto es: 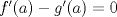
|
|
|
|
 Jun 18 2013, 08:29 PM Jun 18 2013, 08:29 PM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 31-March 12 Desde: Santiago de Chile Miembro Nº: 103.377 Nacionalidad:  Universidad:  Sexo:  |
Haciendo el camino contrario llegas a lo otro
P.D. Una ayudita en latex, para poner las fracciones, pon \frac{numerador}{denominador} Mensaje modificado por José Alejandro Aburto A. el Jun 18 2013, 08:33 PM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 04:34 PM |








