I1 EDO - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Ecuaciones Diferenciales

2 Páginas:

1 2 >

I1 EDO, 1-2013 (José Montero, Alejandro Ramírez, Manuel Elgueta)

Opciones

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 8 2013, 09:40 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />\begin{flushleft}<br />PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE \\<br />FACULTAD DE MATEMATICAS \\<br />DEPARTAMENTO DE MATEMATICAS \\<br />8 de abril de 2013\\<br /><br /><br />\begin{center}<br />MAT1640 - ECUACIONES DIFERENCIALES \\<br />Interrogación N°1 \\<br />\end{center}<br /><br />1. a) (0.75pt) Resuelva el siguiente problema de valores iniciales<br />\begin{center}<br />$\dfrac{dy}{dx}+y tan(x) = cos^2(x)$ \\<br />$y(0) = 1$<br />\end{center}<br /><br /> b) (0.75pt) Resuelva la siguiente ecuación y especifique para que valores de $\beta$ tiene soluciones en todo tiempo<br />\begin{center}<br />$\dfrac{dy}{dt}=1+e^{\beta y}$<br />\end{center}<br /><br />2. a) (0.75pt) Considere la ecuación diferencial<br />\begin{center}<br />$\displaystyle \frac{dy}{dt} +ay=r(t),$<br />\end{center}<br />donde $a$ es una constante real y $r(t)$ es una función continua tal que $\lim_{t\rightarrow\infty}r(t)=0.$ Demuestre que $y(t)$ es una solución de esta ecuación, entonces se tiene que<br />\begin{center}<br />$\lim_{t\rightarrow\infty}y(t)=0.$<br />\end{center}<br /><br />b) (0.75pt) Sea $y(x)$ una solución del problema de valores iniciales<br />\begin{center}<br />$y'=x-y$ \\<br />$y(0)=1.$<br />\end{center}<br /><br />Use el método de Euler con paso $h=\frac{1}{10}$ para encontrar un valor aproximado de $y(x)$ para $x=\frac{1}{10},\frac{2}{10}.$ \newline<br />\newline<br />\end{flushleft}<br />$ Continuo en otro post -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 8 2013, 09:40 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \begin{flushleft}<br />3. (1.5pt) Un cuerpo, cuya temperatura varia con el tiempo, esta roadeado por un mediio que se mantiene a temperatura constante. Denotemos por $T(t)$ la temperatura del cuerpo en el instante $t$. La temperatura constante del medio que rodea al cuerpo la denotamos por $T_{m}$.<br />\newline La Ley del enfriamiento de Newton dice: "La tasa de cambio de la temperatura del cuerpo es proporcional a la diferencia entre la temperatura del cuerpo y la del medio que lo rodea."<br />\newline Se ha medido la temperatura del cuerpo en los tiempo $t=1,\ t=2$ y $t=3$ dando por resultado<br />\begin{center}<br />$T(1)=5, \ T(2)=3$ y $T(3)=2$<br />\end{center}<br />Se sabe que $T(t)\ge T_{m}$ para todo tiempo t. \\<br />Se pide determinar la temperatura $T_{m}$ del medio exterior.<br />\newline<br />\newline<br />4. a) (0.5pt) Determine una función $f(y)$ de modo que el problema de valor iniciales<br />\begin{center}<br />$y'(t)=f(y(t))$ \\<br />$y(0)=1$<br />\end{center}<br />tenga solución única en algun intervalo que contiene a $t=0$. Su respuesta será válida sólo si está debidamente justificada.\\<br />b) (1.0pt) Determine una función $g(y)$ de modo que el problema de valores iniciales<br />\begin{center}<br />$y'(t)=g(y(t))$ \\<br />$y(0)=1$<br />\end{center}<br />tenga al menos dos soluciones en todo intervalo pequeño que contiene a $t=0$. Justifique su respuesta mostrando dos solociones distintas para la función $g$ que escoja.<br />\newline<br />\newline<br />TIEMPO: 2 horas.<br />\end{flushleft}$ Comentario personal: me fue mal xd nos advirtieron que Alejandro Ramírez no le gustan los típicos ejercicios del curso.... tenian razón xd Mensaje modificado por Deac el Apr 9 2013, 03:33 PM -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

Kura Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 8 2013, 10:06 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.918 Registrado: 14-May 08 Desde: The Tower of God Miembro Nº: 23.100 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Salvo el 2a) y el 4), es lo mismo de siempre ;o Supongo que en el 4b) la edo debería ser con g -------------------- Far over... the misty mountains cold. To dungeons deep and caverns old. We must away ere break of day. To find our long-forgotten gold. The pines were roaring on the height. The winds were moaning in the night. The fire was red, it flaming spread. The trees like torches blazed with light. Apunte: Sistemas de Ecuaciones Cuadráticas! Apunte: Series de Fourier! Problemas Resueltos: EDO! OMG! Soy el ñoño de eléctrica.

Zefidu Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 8 2013, 10:22 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 608 Registrado: 18-April 10 Desde: Santiasco Miembro Nº: 69.076 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Solo por aburrimiento... $TEX: \noindent 1a) \newline<br /><br />\noindent Podemos escribir la ED como <br /><br />\begin{equation}y'+y \tan{x} = \cos ^2{x} \end{equation} Es f\'acil darse cuenta que es lineal, por lo que buscamos un factor integrante de la forma \begin{equation} u(x)=e^{\int{\tan{x}dx}} = e^{-\ln{\cos{x}}} = e^{\ln{\sec{x}}} = \sec{x} \end{equation} Multiplicando (2) por (1), <br /><br />\begin{eqnarray}<br />y'\sec{x}+y\tan{x}\sec{x} & = & \cos ^2{x}\sec{x} \\<br />\dfrac{d}{dx}\left(\sec{x} \cdot y \right) & = & \cos{x} \\<br />\sec{x}\cdot y & = & \sin(x) + c \\<br />\Rightarrow y(x) & = & \sin{x}\cos{x} + c\cos{x} \\<br />\end{eqnarray}<br /><br />Usando la condici\'on inicial de $y(0)=1$, tenemos que $y(0)=c=1$, luego la soluci\'on general es $$y(x) = \sin{x}\cos{x} + \cos{x}.$$<br /><br />$ Mensaje modificado por Zefidu el Apr 9 2013, 07:34 PM -------------------- Hold your colours against the wall, When they take everything away, $TEX: $$\int_{0}^{+\infty} {\frac{x^m}{x^n+a}dx} = \frac{1}{a^{\frac{n-m-1}{n}}} \cdot \frac{\pi}{n \sin \left(\frac{(m+1)\pi}{n}\right)}$$$

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 9 2013, 03:32 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kura @ Apr 8 2013, 10:06 PM) Salvo el 2a) y el 4), es lo mismo de siempre ;o Supongo que en el 4b) la edo debería ser con g Gracias ahí edité. La verdad tienes razón, estoy seguro que salve la prueba con los items 1 y 3 xd Ojala haya hecho bien el 2). Y la verdad en el 4) no caché que hacer... sólo escogí justificadamente que mediante el TEyU 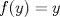$TEX: $f(y)=y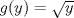$$ y $TEX: $g(y)=\sqrt{y}$$ respectivamente. Mensaje modificado por Deac el Apr 9 2013, 03:35 PM -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 9 2013, 03:56 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Deac @ Apr 8 2013, 09:40 PM) Comentario personal: me fue mal xd nos advirtieron que Alejandro Ramírez no le gustan los típicos ejercicios del curso.... tenian razón xd No lo querrías ver en un curso de teoría de probabilidades o de teoría de la medida... -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 9 2013, 07:32 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kaissa @ Apr 9 2013, 05:56 PM) No lo querrías ver en un curso de teoría de probabilidades o de teoría de la medida... Ahora está haciendo integración. La han visto verde esos cabros con todos los profes que lo han dictado últimamente jaja. -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

febomon Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 9 2013, 08:01 PM Publicado: #8
Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad: Sexo:	CITA(Deac @ Apr 10 2013, 05:02 AM) Gracias ahí edité. La verdad tienes razón, estoy seguro que salve la prueba con los items 1 y 3 xd Ojala haya hecho bien el 2). Y la verdad en el 4) no caché que hacer... sólo escogí justificadamente que mediante el TEyU 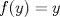$TEX: $f(y)=y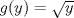$$ y $TEX: $g(y)=\sqrt{y}$$ respectivamente. el truco era agarrar en la 4a) cualquier función con derivada continua en y=1 (asi que esta bien tu funcion), para el 4b tenia que ser una con derivada discontinua en y=1, por ejemplo 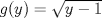$TEX: $g(y)=\sqrt{y-1}$$ que tiene una solucion y=1 y la otra se obtiene separando variables, ( lo siento). Mensaje modificado por febomon el Apr 9 2013, 08:02 PM

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 9 2013, 09:30 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(febomon @ Apr 9 2013, 08:01 PM) el truco era agarrar en la 4a) cualquier función con derivada continua en y=1 (asi que esta bien tu funcion), para el 4b tenia que ser una con derivada discontinua en y=1, por ejemplo 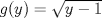$TEX: $g(y)=\sqrt{y-1}$$ que tiene una solucion y=1 y la otra se obtiene separando variables, ( lo siento). Jaja verdad que decia 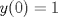$TEX: $y(0)=1$$ fail. Pero me alegraste un poco. daba por hecho que tendría 0 pts. en ese item. -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

« Posterior · Ecuaciones Diferenciales · Anterior »

2 Páginas:

1 2 >

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 07:04 PM