Las 1000 puertas Opciones

[Diego_don_diego]

Mensaje modificado por Diego_don_diego el Feb 27 2013, 05:08 PM

[Diego_don_diego]

Un método para resolver este problema seria analizarlo con un menor numero de puertas.

[Matsimilianito]

Si se le trabaja con diez puertas seria lo mismo que trabajarlo con cien o mil, segun lo que yo pienso, tal vez estoy equivocado.Bueno siguiendo este razonamiento pensaria que cuando va la primera vez abre todas las puertas impares(1,3,5,7,9) de cada diez, hasta mil, deduciendo que la puerta mil queda cerrada. Al volver como la mil es la primera cerrada, se abre, la segunda cerrada queda igual, la tercera cerrada se abre y la cuarta se mantiene cerrada y la quienta cerrada por sucesion tambien se abre, luego aplicamos esto a las primeras 10 puertas y se dice que la ultima puerta cerrada es la cuarta. Estoy en lo correcto o me equivoco?
Pd1: Perdon por los errores de redaccion.
Pd2: Cuando dices "dejan cerrada la cuarta puerta que dejan cerrada" ¿te refieres a que dejan cerrada la cuarta puerta que anteriormente se habia dejado cerrada, o estoy mal? esta confusa esa parte de la redaccion.

Mensaje modificado por Matsimilianito el Mar 30 2013, 09:18 PM

[daniel_esr]

510

No pregunten cómo lo saqué pero la fórmula para el problema de n puertas sería: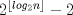


Mensaje modificado por daniel_esr el Apr 1 2013, 09:17 PM

[Azúcar³]

Aquí mi respuesta,

Ya que abrimos la 1, la 3, la 5, etc...hasta la 999 nos quedamos solo con puertas pares (500 puertas)
Ya que hay que abrir la primera que se ve cerrada, asumimos que abrimos la 1000, la 998 queda cerrada, la 996 abierta, la 994 cerrada, la 992 abierta, y notamos cierto patrón, se abren las puertas múltiplos de 4.
Al llegar al inicio nos quedaremos con las puertas pares no múltiplos de 4. (250 puertas)
Ahora, se abre la puerta 2, se deja cerrada la 6, se abre la 10... se abren todas las de la forma 2+8n (2+8*0=2;2+8*1=10)
**Siempre que hayan impares, el número de puertas que quede será el de (n-1)/2
(Y nos quedarán 125 puertas)
Abrimos la 998, dejamos la 990, 982 abierta, 974 cerrada....
Quedando 62 puertas (Esto porque, se abre la primera y la última al ser un número impar, en este caso la puerta 6)
Miramos la 14, solo quedan 62 puertas, 14-30-46...990 (son de la forma 16n-2)
Abrimos la 14, dejamos la 30, abrimos la 46.... hasta dejar la 990 abierta, (quedando cerradas las puertas de la forma 32n-2)
(Nos quedan 31 puertas)
Abrimos la 990, dejamos la 958, abrimos la 926, así hasta abrir la 30 (quedando cerradas las puertas de la forma 64n-2)
**Notamos que se da un patrón de (2 a la algo)-2
(Nos quedan 15 puertas)
(Cerradas las 128n-2)
(Nos quedan 7 puertas)
(Cerradas las 256n-2)
(Nos quedan 3 puertas)
(Cerradas las 512n-2)
(Nos queda 1 puerta)
La de la forma 512n-2 es decir 510
**La única posible pues eran números del 1 al 1000

Espero les guste, eso.

[Diego_don_diego]

510

No pregunten cómo lo saqué pero la fórmula para el problema de n puertas sería:

¿Como llegaste a eso?