I4 Cálculo II TAV 2013 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Cálculo II

Reply to this topic

Start new topic

I4 Cálculo II TAV 2013

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 5 2013, 01:30 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Adjunto la I4 del TAV 2013. Esta fue la prueba que menos me gustó, siento como qué no midió nada xd. I4_2013_TAV.png ( 2.69mb ) Número de descargas: 68 Saludos! -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

Kura Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 5 2013, 01:46 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.918 Registrado: 14-May 08 Desde: The Tower of God Miembro Nº: 23.100 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	1c) Para que llegue al origen solo ocurre en 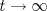$TEX: $t \to \infty$$ , de esta forma la distancia recorrida será la longitud de arco de la curva. Notemos que 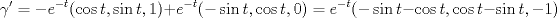$TEX: $$\gamma' = -e^{-t}(\cos t, \sin t, 1) + e^{-t} (-\sin t, \cos t, 0) = e^{-t}(-\sin t - \cos t, \cos t - \sin t, -1)$$$ Luego 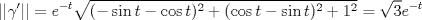$TEX: $$ \|\|\gamma'\|\| = e^{-t} \sqrt{ (-\sin t - \cos t)^2 + (\cos t - \sin t)^2 + 1^2 } = \sqrt{3} e^{-t}$$$ De esta forma la distancia recorrida es: 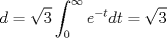$TEX: $$d = \sqrt{3} \int_0^\infty e^{-t} dt = \sqrt{3}$$$ Espero no haberme pifiado xd -------------------- Far over... the misty mountains cold. To dungeons deep and caverns old. We must away ere break of day. To find our long-forgotten gold. The pines were roaring on the height. The winds were moaning in the night. The fire was red, it flaming spread. The trees like torches blazed with light. Apunte: Sistemas de Ecuaciones Cuadráticas! Apunte: Series de Fourier! Problemas Resueltos: EDO! OMG! Soy el ñoño de eléctrica.

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 5 2013, 02:05 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kura @ Feb 5 2013, 01:46 PM) 1c) Para que llegue al origen solo ocurre en 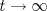$TEX: $t \to \infty$$ , de esta forma la distancia recorrida será la longitud de arco de la curva. Notemos que 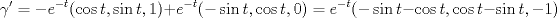$TEX: $$\gamma' = -e^{-t}(\cos t, \sin t, 1) + e^{-t} (-\sin t, \cos t, 0) = e^{-t}(-\sin t - \cos t, \cos t - \sin t, -1)$$$ Luego 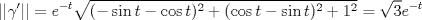$TEX: $$ \|\|\gamma'\|\| = e^{-t} \sqrt{ (-\sin t - \cos t)^2 + (\cos t - \sin t)^2 + 1^2 } = \sqrt{3} e^{-t}$$$ De esta forma la distancia recorrida es: 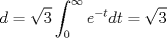$TEX: $$d = \sqrt{3} \int_0^\infty e^{-t} dt = \sqrt{3}$$$ Espero no haberme pifiado xd Esta bien! de hecho así mismo lo hice! -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 5 2013, 07:26 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Están bien entretes las pruebas. Un poco distintas a lo que se suele preguntar durante un semestre normal. -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Logan_Wayne Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 5 2013, 09:02 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 282 Registrado: 12-January 13 Desde: Bati-Escuela de Charles Xavier. Miembro Nº: 114.884 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \textbf{[P2]} Primero, $\vec{\varphi}(t) = \vec{\gamma}\,'(t) = (3t\,,\,3t^2\,,\,kt^3)\,' = (3\,,\,6t\,,\,3kt^2)$, con $k\in\mathbb{R}$.$ $TEX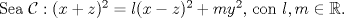: Sea ${\cal C}: (x+z)^2 = l(x-z)^2+my^2$, con $l,m\in\mathbb{R}$.$ $TEX: Como $\varphi(t)\in{\cal C}$, $(3+3kt^2)^2 = l(3-3kt^2)^2 + 36mt^2 \Leftrightarrow t^4[9k^2 - 9lk^2] + t^2[18k + 18kl - 36m] + 9-9l = 0$$ $TEX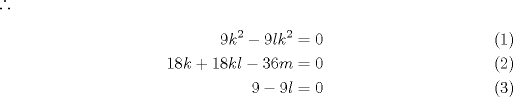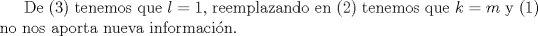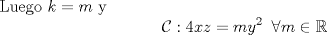: $\therefore$\begin{align}<br />9k^2-9lk^2 &= 0 \\<br />18k+18kl-36m &= 0 \\<br />9-9l &= 0<br />\end{align}$ $TEX: De $(3)$ tenemos que $l=1$, reemplazando en $(2)$ tenemos que $k=m$ y $(1)$ no nos aporta nueva informaci\'on.$ $TEX: Luego $k=m$ y $${\cal C}: 4xz = my^2\;\; \forall m\in\mathbb{R}$$$ --------------------

« Posterior · Cálculo II · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 10:24 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.