Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> Control I Matematica III 2013
Gioia
mensaje Jan 11 2013, 05:11 PM
Publicado: #1


Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 31
Registrado: 25-September 12
Miembro Nº: 111.257
Nacionalidad:
Universidad: Universidad de Chile-FCFM
Sexo:






jpt_chileno.gif

Mensaje modificado por Gioia el Jan 11 2013, 05:11 PM
Go to the top of the page
 
+Quote Post
Kreator
mensaje Jan 12 2013, 12:14 AM
Publicado: #2


Dios Matemático
Ícono de Grupo

Grupo: Super Moderador
Mensajes: 261
Registrado: 12-February 11
Miembro Nº: 83.790
Nacionalidad:
Colegio/Liceo: Preuniversitario Pedro de Valdivia
Universidad: Universidad Catolica de Chile-Facultad de Ingenieria
Sexo:



TEX: Para P2 a) definiciones y recordar conjunto universo, para P2 b), descomponer la equivalencia en implicancias. Los de lógica estaban regalados.<br />Como noción, para el P3 b), para la inyectividad, ver que pasa cuando $\delta_A(x)=\delta_B(x)$ (para $A$ y $B$ elementos de $P(E)$), imponer que sean iguales a 1 y 0, y asumir que $x \in A$, y ver que pasa (recordar que tiene que pasar para que dos conjuntos sean iguales, que es lo que queremos demostrar)<br />


--------------------
Go to the top of the page
 
+Quote Post
mpipe
mensaje Jan 12 2013, 02:32 AM
Publicado: #3


Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 52
Registrado: 15-May 09
Miembro Nº: 51.306
Nacionalidad:
Colegio/Liceo: Colegio Alcantara de la Florida
Universidad: Universidad de Chile-FCFM
Sexo:



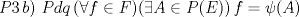TEX: $P3\, b)\,\, Pdq \, (\forall f \in F)(\exists A \in P(E))\, f=\psi(A)$
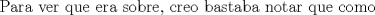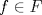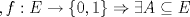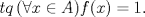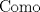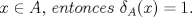TEX: Para ver que era sobre, creo bastaba notar que como TEX: $f \in F$TEX: $,f: E \rightarrow \{0,1\} \Rightarrow \exists A \subseteq E$ TEX: $\,tq\,(\forall x \in A) f(x) = 1.$ TEX: Como TEX: $\,x \in A, \,entonces\, \,\delta_{A}(x) = 1 .$
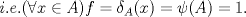TEX: $i.e. (\forall x \in A) f= \delta_{A}(x)=\psi(A) = 1.$
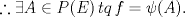TEX: $\therefore \exists A \in P(E)\, tq\, f=\psi(A).$
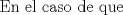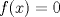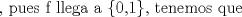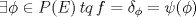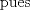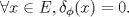TEX: En el caso de que TEX: $f(x)=0$ TEX: , pues f llega a \{0,1\}, tenemos que TEX: $\exists\phi\in P(E)\,tq\,f=\delta_{\phi}=\psi(\phi)$ TEX: pues TEX: $\forall x \in E, \delta_{\phi}(x)=0.$

Espero que esté bien zippymmm.gif y si alguien se da cuenta de que no, que me avise para arreglarlo xD


--------------------
Solo para gente aburrida.




EDV Matemática I ✔, Matemática II ✔, Matemática III ✔





Mechón 2013
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 24th November 2024 - 12:31 AM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.