|
|
|
|
|
|
|
  |
 Apr 22 2007, 01:54 PM Apr 22 2007, 01:54 PM
Publicado:
#1
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 163 Registrado: 5-August 06 Desde: Concepción, Octava región. Miembro Nº: 1.853 Nacionalidad:  Colegio/Liceo:  Sexo:  |
  : La circunferencia de ecuación : La circunferencia de ecuación 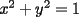 , intersecta la recta , intersecta la recta 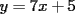 en dos puntos diferentes en dos puntos diferentes  y y  . Sea . Sea  el centro de la circunferencia. Encontrar la medida del el centro de la circunferencia. Encontrar la medida del  AOB AOB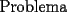  : Sean : Sean  , ,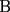 , , 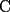 , ,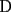 y y 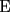 cinco puntos en el plano con AB=21,BC=17,CD=14,DE=67 y EA=15. Encontrar el valor de AD. cinco puntos en el plano con AB=21,BC=17,CD=14,DE=67 y EA=15. Encontrar el valor de AD.  : Encontrar todos los números enteros : Encontrar todos los números enteros  , tales que , tales que 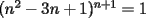   : Utilizando varios cubos pequeños iguales, se forma un cubo grande. El abuelo Anacleto, matemático jubilado, pinta de rojo algunas de las caras de este cubo grande. Luego, desarma el cubo. Resulta que 45 de los cubos pequeños no tienen pintura roja en ninguna de sus caras. Determinar cuántos cubos pequeños usó el abuelo Anacleto. : Utilizando varios cubos pequeños iguales, se forma un cubo grande. El abuelo Anacleto, matemático jubilado, pinta de rojo algunas de las caras de este cubo grande. Luego, desarma el cubo. Resulta que 45 de los cubos pequeños no tienen pintura roja en ninguna de sus caras. Determinar cuántos cubos pequeños usó el abuelo Anacleto.  : Seam : Seam  , , 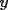 y y  números reales que números reales que 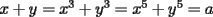 . Determinar todos los valores posibles para . Determinar todos los valores posibles para  Opinen que les parecio la nueva modalidad de esta nueva prueba grupal. Saludos.! Mensaje modificado por alvaro el Apr 22 2007, 02:24 PM -------------------- "Me esfuerzo por ser mejor; y no él mejor" A.Flores
|
|
|
|
 Apr 22 2007, 02:02 PM Apr 22 2007, 02:02 PM
Publicado:
#2
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 90 Registrado: 22-April 07 Desde: Santiago, Chile. Miembro Nº: 5.383 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Disculpa pero esta es la primera vez que participo en esto y quisiese saber como era antes. ¿Alguien me podría explicar?... gracias.
-------------------- |
|
|
|
 Apr 22 2007, 02:33 PM Apr 22 2007, 02:33 PM
Publicado:
#3
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 163 Registrado: 5-August 06 Desde: Concepción, Octava región. Miembro Nº: 1.853 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Disculpa pero esta es la primera vez que participo en esto y quisiese saber como era antes. ¿Alguien me podría explicar?... gracias. Con respecto a tu pregunta; Yo participe el año pasado igual y las pruebas grupales eran más libre, ya que se entregaba una lista de preguntas(de un tema determinado) por equipos, y él propio grupo decidia como la resolvía; no habian restricciones(como ahora) ni pistas y también había más tiempo. Revisa las pruebas grupales de los años anteriores, para que te quede más claro. Saludos.! -------------------- "Me esfuerzo por ser mejor; y no él mejor" A.Flores
|
|
|
|
 Apr 22 2007, 02:36 PM Apr 22 2007, 02:36 PM
Publicado:
#4
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 Separamos las ecuaciones a conviniencia y tenemos: 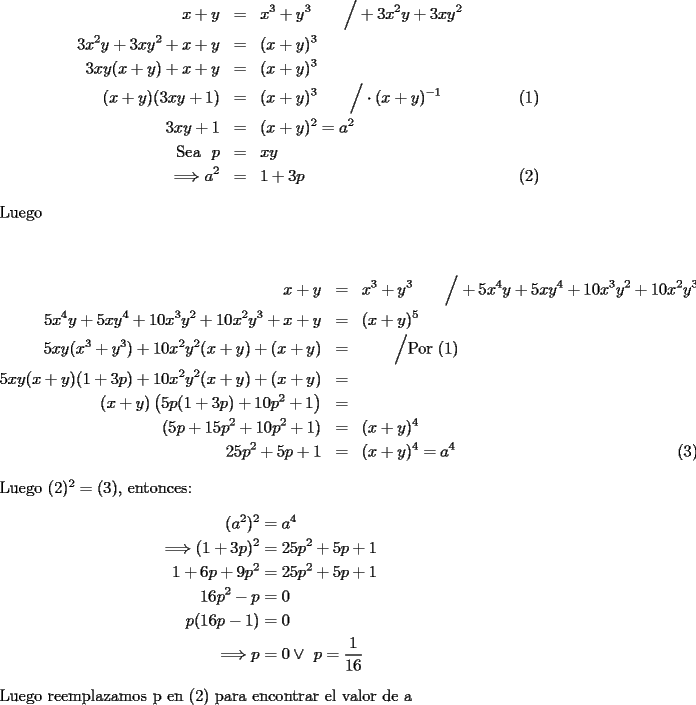 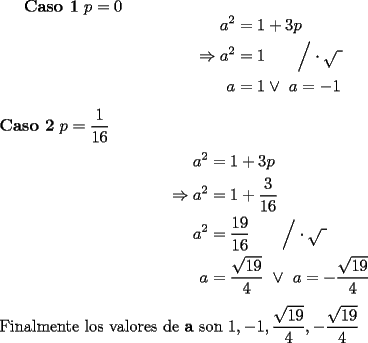 Antes las pruebas eran mas problemas y se hacian entre los 5 del grupo, se converzaba (se comia) y se leseaba harto, pero salian buenos resultado, entre los mas memorables me acuerdo del estudio de los cuadrados magicos y de la regla sin fin. --------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Apr 22 2007, 03:09 PM Apr 22 2007, 03:09 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

-------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"-
Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo.. |
|
|
|
 Apr 22 2007, 03:45 PM Apr 22 2007, 03:45 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"-
Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo.. |
|
|
|
 Apr 22 2007, 03:46 PM Apr 22 2007, 03:46 PM
Publicado:
#7
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"-
Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo.. |
|
|
|
 Apr 22 2007, 04:05 PM Apr 22 2007, 04:05 PM
Publicado:
#8
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 90 Registrado: 22-April 07 Desde: Santiago, Chile. Miembro Nº: 5.383 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Respecto a lo dicho por zirou del problema 5(no me funciono el quote).
El 0, -2 y +2 es también son soluciónes posibles de a. Si x=2 y y=-2 (x=-y), por ejemplo. 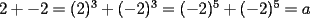 Reemplazamos... 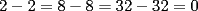 Oh, y lo olvidaba, si x=-1 e y-1 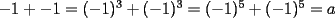 Reemplazamos... 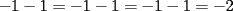 Finalmente, si x=1 e y=1 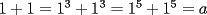 Resolvemos... 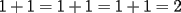 No me preguntes por una solucion algebraica como la tuya, porque no la tengo. Simplemente encontre los números al tanteo y me dió. De este mismo modo pude comprobar que -1 y +1 son soluciones posibles. Mensaje modificado por Helios el Apr 22 2007, 04:12 PM -------------------- |
|
|
|
 Apr 22 2007, 04:17 PM Apr 22 2007, 04:17 PM
Publicado:
#9
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Respecto a lo dicho por zirou del problema 5(no me funciono el quote). El 0, -2 y +2 es también son soluciónes posibles de a. Si x=2 y y=-2 (x=-y), por ejemplo. 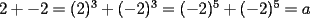 Reemplazamos... 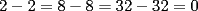 Oh, y lo olvidaba, si x=-1 e y-1 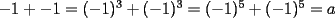 Reemplazamos... 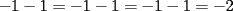 Finalmente, si x=1 e y=1 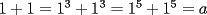 Resolvemos... 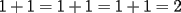 No me preguntes por una solucion algebraica como la tuya, porque no la tengo. Simplemente encontre los números al tanteo y me dió. De este mismo modo pude comprobar que -1 y +1 son soluciones posibles. eso corresponde a x=-y que tambien me dio algebraicamente, pero en el apuro de traspasar (pues me nuble un poco) se me quedo en el tintero gracias por la correccion, tratare de buscar dichas soluciones (que ya creo saber por donde van) --------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Apr 22 2007, 05:50 PM Apr 22 2007, 05:50 PM
Publicado:
#10
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 125 Registrado: 15-October 06 Desde: Concepción Miembro Nº: 2.518 Nacionalidad:  Sexo:  |
Soy de nivel M1 y no voy a responder, pero si voy a dar mi humirde opinion.
Creo que se perdio el trabajo de grupo del año pasado, pero, a pesar de que muchos creen que no hay trabajo en equipo, creo yo que si lo hay. Primero al elejir qué pregunta realizara cada uno, y luego saber a quien se le entregaran las pistas, y a quien se le ayudara cuando llegue dicha ocacion. El equipo que no logre dominar estos puntos, no podra obtener buenos resultados en la competencia. Esperando que esto les pueda servir, me despido. Gracias. -------------------- Campeón, campeón
campeón hay por montones hinchada hay una sola es la de la U GRANDE LA U VIVA CHILE "Estudiar, no para saber más, sino para servir mejor". Santo Domingo de Guzmán. El hombre es el único ser vivo que tropieza dos veces con la misma piedra. El hombre fuerte no es aquel que no se cae; es aquel que sabe levantarse. El hombre más valiente no es aquel que no tiene miedos; es aquel que no teme en enfrentarlos. La derrota es una posibilidad, pero nunca será una opción. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 26th April 2025 - 12:40 PM |