|
|
|
|
|
|
|
  |
 Apr 22 2007, 01:11 AM Apr 22 2007, 01:11 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad:  Universidad:  Sexo:  |
--------------------    |
|
|
|
 Apr 22 2007, 06:14 PM Apr 22 2007, 06:14 PM
Publicado:
#2
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 27 Registrado: 31-October 05 Miembro Nº: 355 |
Bueno, aqui van mis soluciones para la prueba, no se si esten totalmente buenas, pero al menos serviran para iniciar la discusion:
Problema 1: Si llamamos x1,x2,x3,x4,x5,x6,x7,x8,x9 a la ditribucion escogida por A, de los elementos del conjunto {1,2,3,4,5,6,7,8,9} sin repeticiones, notaremos que el resultado que se obtendra sera: r= x1±|(x2+x4+x6+x8)-(x3+x5+x7+x9)| para simplificar, si llamamos P=x2+x4+x6+x8 y Q=x3+x5+x7+x9, entonces r=x1±|P-Q| Ahora bien, el signo ± representa la desicion de B, pero como este desea obtener el menor valor posible en el resultado, siempre partira con un signo (que van alternados), de tal forma que el resultado de ±|P-Q| sea negativo, luego, el resultado simplemente será: r=x1-|P-Q| Para que A pueda maximizar esto, debe exoger x1 máximo, y |P-Q| mínimo, esto es: x1=max{1,2,3,4,5,6,7,8,9}=9 y |P-Q|=0 (lo que es posible como se ve enseguida) una forma de obtener |P-Q|=0, seria P=1+4+5+8=18 y Q=2+3+6+7=18 o vicerversa de cualquier forma, el resultado maximo que puede obtener A, suponiendo que B utiliza su mejor estrategia, es r=9 ...bueno, el otro problema que fue el que mas tiempo me tuvo pensando (dada mi falta de practica =/), aunque finalmente me salio, lo resolvi basicamente aplicando pitagoras y el teorema de la bisetriz, y prolongando AK hasta su interseccion con CD ... vere si puedo subir un dibujo o algo asi saludos desde el humilde pueblo de Antofa =P |
|
|
|
 Apr 22 2007, 06:32 PM Apr 22 2007, 06:32 PM
Publicado:
#3
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
|
|
|
|
 Apr 22 2007, 07:07 PM Apr 22 2007, 07:07 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
R1 Notemos que el primer numero que se coloca en la figura siempre es positivo, asi que si
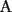 quiere maximizar el resultado debe colocar el mayor en ese lugar, osea el quiere maximizar el resultado debe colocar el mayor en ese lugar, osea el  . .Sea 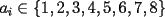 tal que ningun tal que ningun 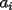 es igual a otro, nos queda algo así: es igual a otro, nos queda algo así: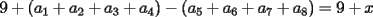 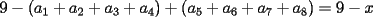 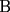 elige una de las dos a conveniencia. elige una de las dos a conveniencia.Notemos que 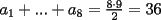 así que podemos dividirla en dos grupos de igual suma, notemos que si así que podemos dividirla en dos grupos de igual suma, notemos que si  es diferente de es diferente de  , , 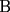 siempre puede hacer que el resultado sea menor que siempre puede hacer que el resultado sea menor que  , pero si , pero si 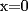 no, ósea este caso maximiza. no, ósea este caso maximiza.Luego 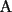 debe hacer de la siguiente forma su elección: debe hacer de la siguiente forma su elección: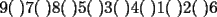 y el resultado es  . .
Mensaje modificado por iMPuRe el Apr 22 2007, 07:09 PM -------------------- |
|
|
|
 Apr 22 2007, 07:09 PM Apr 22 2007, 07:09 PM
Publicado:
#5
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
R2
 Notemos los angulos, copiemos el 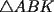 en en 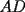 , notemos que el , notemos que el 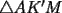 es isoceles en es isoceles en 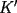 con lo que se prueba lo pedido. con lo que se prueba lo pedido.
-------------------- |
|
|
|
 Apr 23 2007, 08:40 AM Apr 23 2007, 08:40 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ya tenemos la prueba resuelta en su totalidad. Por razones de tiempo, sólo he leído las primeras dos soluciones: están perfectas, lo que implica (entre otras cosas) que se entienden bien...
Confirmen o desmientan lo que estoy pensando, pero el segundo problema es una vulgar copia de un problema en algún lado (mas no recuerdo de dónde). El primer problema lo propuse yo, fue algo que se me ocurrió durante las "vacaciones", no tan complicado, y que no recordaba haberlo visto en algún lado Saludos -------------------- |
|
|
|
 Apr 23 2007, 04:41 PM Apr 23 2007, 04:41 PM
Publicado:
#7
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ya tenemos la prueba resuelta en su totalidad. Por razones de tiempo, sólo he leído las primeras dos soluciones: están perfectas, lo que implica (entre otras cosas) que se entienden bien... Confirmen o desmientan lo que estoy pensando, pero el segundo problema es una vulgar copia de un problema en algún lado (mas no recuerdo de dónde). El primer problema lo propuse yo, fue algo que se me ocurrió durante las "vacaciones", no tan complicado, y que no recordaba haberlo visto en algún lado Saludos Absolutamente de acuerdo, las malas lenguas dicen que el P2 de esta prueba es un conocidísimo problema de la OMA. Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Apr 23 2007, 07:16 PM Apr 23 2007, 07:16 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Absolutamente de acuerdo, las malas lenguas dicen que el P2 de esta prueba es un conocidísimo problema de la OMA. Saludos Es mas... en una guia por ahi que se titulaba "GUIA TRABAJO CLASE Nº 1, INTRODUCCION A PROBLEMAS DE OLIMPIADAS" es el Problema 9. Mensaje modificado por iMPuRe el Apr 23 2007, 07:18 PM -------------------- |
|
|
|
 Apr 18 2008, 04:19 AM Apr 18 2008, 04:19 AM
Publicado:
#9
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 14-January 08 Desde: Estadio Maracaná, Río de Janeiro, y en Chile. Miembro Nº: 14.654 Nacionalidad:  Sexo:  |

Mensaje modificado por xuncoco el Apr 19 2008, 10:44 AM --------------------  pato style... |
|
|
|
 Apr 19 2008, 10:57 AM Apr 19 2008, 10:57 AM
Publicado:
#10
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 14-January 08 Desde: Estadio Maracaná, Río de Janeiro, y en Chile. Miembro Nº: 14.654 Nacionalidad:  Sexo:  |
Ahora bien, el signo ± representa la desicion de B, pero como este desea obtener el menor valor posible en el resultado, siempre partira con un signo (que van alternados), de tal forma que el resultado de ±|P-Q| sea negativo, luego, el resultado simplemente será: r=x1-|P-Q| es verdad que B elige que el resultado de ±|P-Q| sea negativo, pero no sabes si P>Q o Q>P. el signo que elegiste tú fue para P>Q, porque para Q>P tienes que P-Q es negativo, luego debes poner "+". notemos que si  es diferente de es diferente de  , , 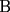 siempre puede hacer que el resultado sea menor que siempre puede hacer que el resultado sea menor que  , pero si , pero si 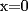 no, ósea este caso maximiza. no, ósea este caso maximiza.¿y no puedes hacer x positivo? ¿por qué tiene que ser 0? saludos, cuates revisen mi solución =D --------------------  pato style... |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:49 PM |














