|
|
|
|
|
|
|
  |
 Dec 7 2012, 07:38 PM Dec 7 2012, 07:38 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 1-September 09 Miembro Nº: 58.083 Nacionalidad:  Sexo:  |
Quisiera pedir ayuda, por apuro no se si estará en el lugar correcto. Necesito probar que el conjunto
A={(x,y)/ x+y>1}, es conjunto abierto. Si bien tengo una idea, no logro calzar una explicación. Espero puedan ayudarme. Mensaje modificado por NeManz el Dec 7 2012, 07:39 PM |
|
|
|
 Dec 7 2012, 08:21 PM Dec 7 2012, 08:21 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 255 Registrado: 7-October 10 Miembro Nº: 78.381 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Puedes tomar un punto del conjunto y otro punto cualquiera y establecer que su distancia es menor a épsilon (cualquier norma), y en base a eso debes llegar a concluir que el punto cualquiera pertenece también a tu conjunto.
--------------------   |
|
|
|
 Dec 7 2012, 08:38 PM Dec 7 2012, 08:38 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 618 Registrado: 8-June 08 Desde: Paris Miembro Nº: 26.525 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
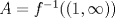 con con 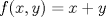 (que es claramente continua). (que es claramente continua).
-------------------- ¡Por más representación, vota Riesz!
|
|
|
|
 Dec 7 2012, 08:39 PM Dec 7 2012, 08:39 PM
Publicado:
#4
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 1-September 09 Miembro Nº: 58.083 Nacionalidad:  Sexo:  |
Por lo que me explicaron tengo esto:
Un conjunto A es abierto si: dado p(x,y) en A, existe r>0 tal que B(p,r) es subconjunto de A... Dado esa definición, como encuentro y defino el r que necesito? |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 06:08 PM |









