I3 Calculo I - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Cálculo I

4 Páginas:

< 1 2 3 4 >

Reply to this topic

Start new topic

I3 Calculo I, 2S 2012

andreanthua Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 19 2012, 11:16 PM Publicado: #11
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.525 Registrado: 13-July 10 Desde: Santiago, Chile Miembro Nº: 74.135 Nacionalidad: Universidad: Sexo:	CITA(Leonardo Mauricio @ Nov 19 2012, 11:12 PM) El 2a no tiene mayores complicaciones sólo se requiere ser ordenado y La 2b es directa, pues es gamma de 3 En el 4) no debieron haber tenido mayores complicaciones pues son problemas del tipo calcule El 3) se nota que es laaaaaargo al igual que el 1 Jaja me estai hueveando, no sabemos gamma. -------------------- Stay hungry. Stay foolish ahorroClicks

javierch14 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 19 2012, 11:17 PM Publicado: #12
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 11-November 10 Desde: Santiago Miembro Nº: 80.141 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	En la 5a apliqué lhopital mal sin querer.... XD sabia que era 0/0 y despues pase dividiendo el x para que no estorvara con la integral...será. CITA(Leonardo Mauricio @ Nov 19 2012, 11:12 PM) El 2a no tiene mayores complicaciones sólo se requiere ser ordenado y La 2b es directa, pues es gamma de 3 En el 4) no debieron haber tenido mayores complicaciones pues son problemas del tipo calcule El 3) se nota que es laaaaaargo al igual que el 1 gamma de 3? quisawea Mensaje modificado por javierch14 el Nov 19 2012, 11:19 PM -------------------- Estudiante de Ingeniería Civil Industrial, mención Tecnologías de Información. Un Cover de Pantera en HD, con algunos errores :(

andreanthua Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 19 2012, 11:21 PM Publicado: #13
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.525 Registrado: 13-July 10 Desde: Santiago, Chile Miembro Nº: 74.135 Nacionalidad: Universidad: Sexo:	Hey, por si acaso el 5a sí me da 2, al igual que la 2b. -------------------- Stay hungry. Stay foolish ahorroClicks

Leonardo Maurici... Leonardo Mauricio Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 19 2012, 11:42 PM Publicado: #14
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.244 Registrado: 11-October 09 Desde: Santiago Miembro Nº: 60.148 Nacionalidad: Universidad: Sexo:	Función Gamma vean la definición y verán que es directo xD -------------------- CITA(Marcel Claude @ Oct 13 2013, 22:10 PM) Venezuela es más democrático que Chile XD CITA(luismema @ Dec 6 2012, 05:48 PM) CITA(Exorcista @ Dec 6 2012, 05:39 PM) x1000 ... a tipos como este me refiero cuando hablo de ''ingenieros beauchef frustrados'', que lata...... compadre vaya a la escuela de psicologia de la U, ya que le queda cerquita y pide hora, por que de verdad del tiempo que he estado en el foro, usted no aporta mucha. Pd: ademas hablas y discriminas a la gente de otra U como si las conocieras, tu no pareces ser de la usach. Si aveiguo algo que te sirva respecto a lo de salud, te lo informo. CITA(master_c @ Sep 23 2012, 12:11 PM) (a Kaissa) 6528 post sin decir nada, solo criticar en un foro que es para ayudar, proponer y resolver (compartir conocimiento) y me hablas de malgastar la vida :death: CITA(clowny @ Sep 11 2012, 03:45 PM) jajajajajja, no me voy a rebajar a pelear con alguien dice que usa mac en su pc (si mac) jajajaja. win2 va a caher junto a mac tarde o temprano, esa es mi opinión :) CITA(Kura @ Jun 7 2012, 01:13 PM) El mecanismo de evaluación es así, obtener buenas notas es posible aprovechando los bugs del sistema. CITA(Gastón Burrull @ Apr 27 2012, 11:15 PM) CITA(clowny @ Apr 27 2012, 11:10 PM) Sería re fome el mundo lleno de físicos y matemáticos... Seguro que tienes internet y computadora gracias a la numerología... CITA(VA Jiménez @ Dec 28 2011, 04:28 PM) ya que hablas de mediocridad, el criticar eso es, por decir lo menos, mediocre. CITA(VA Jiménez @ Dec 28 2011, 04:28 PM) y que te rías de eso me parece bastante penoso, Mr. "Estoy haciendo un doctorado y lo menciono en 5 de cada 6 post" (dirigido a Sansanito) CITA(anonimo @ Dec 28 2011, 04:35 PM) pd: xD he leido muuchos post de Sansanito y recién ahora sé que estudia un doctorado xD (y eso que hemos hablado por pm) CITA(clowny @ Jan 27 2011, 09:35 PM) ...hablé de que el liberalismo de smith en alguna parte era mejor que el neoliberalismo, y se mal interpretó con eso... RE: Simplemente en ninguna parte.... CITA(clowny @ Jan 27 2011, 09:43 PM) Imaginate llevan al mod, a mxmaster y a yarly a hablar del modelo economico moderno ohmy.gif! RE: Me imagino a clowny en las mismas... CITA(El Geek @ Jan 27 2012, 01:57 PM) Notable que tu siendo un chanta que no salva a nadie (porque en el foro no has mostrado jamás tener alguna destreza con mate sino que puro blablá) sigas viniendo a trollear dándoteas de capo.

andreanthua Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 19 2012, 11:47 PM Publicado: #15
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.525 Registrado: 13-July 10 Desde: Santiago, Chile Miembro Nº: 74.135 Nacionalidad: Universidad: Sexo:	CITA(Leonardo Mauricio @ Nov 19 2012, 11:42 PM) Función Gamma vean la definición y verán que es directo xD Oooh verdad! -------------------- Stay hungry. Stay foolish ahorroClicks

ingeniero 333 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 20 2012, 01:39 AM Publicado: #16
Matemático Grupo: Usuario FMAT Mensajes: 59 Registrado: 14-December 11 Miembro Nº: 99.201 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	que les dio la 2a)? otra cosa, por que la 2b les da -2? si dice que R tiende a infinito, segun yo el limite era 0 Mensaje modificado por ingeniero 333 el Nov 20 2012, 02:43 AM

ingeniero 333 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 20 2012, 02:45 AM Publicado: #17
Matemático Grupo: Usuario FMAT Mensajes: 59 Registrado: 14-December 11 Miembro Nº: 99.201 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(W Campbell @ Nov 20 2012, 02:43 AM) p2) comentarios de solución: a) Aplicar exp(ln(x))) y prodremos derivar funciones del tipo a^x, x^f(x) etc....despues aplicar regla de la cadena...etc. b)Aplicar teorema vaca, U=x^2, dv=exp(-x)dx, siempre con la finalidad de disminuir el exponente del polinomio (en este caso el monomio x^2) Perfecto! tengo exactamente lo mismo. En la 2b, al ingresar ese limite a una calculadora de limites te da que es 0

ingeniero 333 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 20 2012, 02:50 AM Publicado: #18
Matemático Grupo: Usuario FMAT Mensajes: 59 Registrado: 14-December 11 Miembro Nº: 99.201 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	la 5a) también me dio 2 la 3 me dio esos valores de las letras también, pero parece que la tengo mala porque la hice entera con otros valores me di cuenta de eso 5 minutos antes y encontre los valores correctos y no alcance a cambiar todo

javierch14 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 20 2012, 06:09 AM Publicado: #19
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 195 Registrado: 11-November 10 Desde: Santiago Miembro Nº: 80.141 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(ingeniero 333 @ Nov 20 2012, 01:39 AM) que les dio la 2a)? otra cosa, por que la 2b les da -2? si dice que R tiende a infinito, segun yo el limite era 0 CITA(W Campbell @ Nov 20 2012, 02:43 AM) p2) comentarios de solución: a) Aplicar exp(ln(x))) y prodremos derivar funciones del tipo a^x, x^f(x) etc....despues aplicar regla de la cadena...etc. b)Aplicar teorema vaca, U=x^2, dv=exp(-x)dx, siempre con la finalidad de disminuir el exponente del polinomio (en este caso el monomio x^2) Ojo que en la 2b la integral iba de 0 a R, y al remplazar con la integral de e^-x salia un 2e^0, que es 2.. Mensaje modificado por javierch14* el Nov 20 2012, 06:09 AM -------------------- Estudiante de Ingeniería Civil Industrial, mención Tecnologías de Información. Un Cover de Pantera en HD, con algunos errores :(

manzanin	Nov 20 2012, 10:41 AM Publicado: #20
Invitado	Voy a lanzarme con la P1. Me tinca que está mal la weá si La mejor forma de visualizar esto es graficando, así que fijemos nuestra mirada en la figura adjunta. garf.png ( 5.95k ) Número de descargas: 4 Calculemos el área de cada cuadrilátero. Para ellos debemos recordar que el área de un trapecio es: 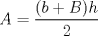$TEX: $$A=\frac{(b+B)h}{2}$$$ Luego, si llamanos Ti al área del trapecio de Base mayor f(xi), entonces, no es difícil notar que 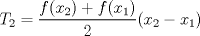$TEX: $$T_{1}=\frac{f(x_{1})+f(x_{0})}{2}(x_{1}-x_{0})$$$ , $TEX: $$T_{2}=\frac{f(x_{2})+f(x_{1})}{2}(x_{2}-x_{1})$$$ y así. El área total abarcada por los trapecios será entonces: 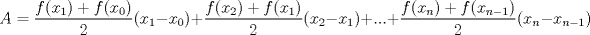$TEX: $$A=\frac{f(x_{1})+f(x_{0})}{2}(x_{1}-x_{0})+\frac{f(x_{2})+f(x_{1})}{2}(x_{2}-x_{1})+...+\frac{f(x_{n})+f(x_{n-1})}{2}(x_{n}-x_{n-1})$$$ Notemos, sin embargo, que como la división de x es regular 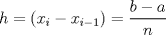$TEX: $$h=(x_{i}-x_{i-1})=\frac{b-a}{n}$$$ Y más aún, notemos que: 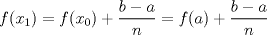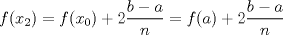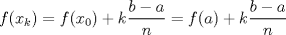$TEX: $$f(x_{1})=f(x_{0})+\frac{b-a}{n}=f(a)+\frac{b-a}{n}$$$ $TEX: $$f(x_{2})=f(x_{0})+2\frac{b-a}{n}=f(a)+2\frac{b-a}{n}$$$ $TEX: $$f(x_{k})=f(x_{0})+k\frac{b-a}{n}=f(a)+k\frac{b-a}{n}$$$ Con esto: 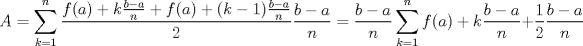$TEX: $$A=\sum\limits_{k=1}^{n}{\frac{f(a)+k\frac{b-a}{n}+f(a)+(k-1)\frac{b-a}{n}}{2}}\frac{b-a}{n}=\frac{b-a}{n}\sum\limits_{k=1}^{n}{f(a)+k}\frac{b-a}{n}+\frac{1}{2}\frac{b-a}{n}$$$ Luego, como el área bajo una función es la integral de la función 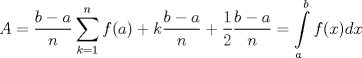$TEX: $$A=\frac{b-a}{n}\sum\limits_{k=1}^{n}{f(a)+k}\frac{b-a}{n}+\frac{1}{2}\frac{b-a}{n}=\int\limits_{a}^{b}{f(x)dx}$$$ Para 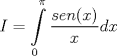$TEX: $$I=\int\limits_{0}^{\pi }{\frac{sen(x)}{x}}dx$$$ , $TEX: $$[a,b]=[0,\pi ]$$$ Considerando n=4, se tiene: $TEX: $$\int\limits_{0}^{\pi }{\frac{sen(x)}{x}dx}=\frac{\pi }{4}\sum\limits_{k=1}^{4}{f(a)+k}\frac{\pi }{4}+\frac{\pi }{8}=\frac{\pi }{4}\left[ 4f(a)+6\frac{\pi }{4}+4\frac{\pi }{8} \right]$$$ Recordemos, sin embargo, que: 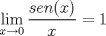$TEX: $$\underset{x\to 0}{\mathop{\lim }}\,\frac{sen(x)}{x}=1$$$ Con eso, la cuestion final queda: $TEX: $$I=\frac{\pi }{4}\left[ 4+\frac{3}{2}\pi +\frac{1}{2}\pi \right]=\frac{\pi }{4}\left[ 2\pi +4 \right]$$$

« Posterior · Cálculo I · Anterior »

4 Páginas:

< 1 2 3 4 >

Reply to this topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 04:53 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.