|
|
|
|
|
|
|
  |
 Nov 16 2012, 10:17 AM Nov 16 2012, 10:17 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- |
|
|
|
 Feb 18 2014, 10:33 PM Feb 18 2014, 10:33 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 1: Como
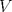 es vecindad débil de es vecindad débil de  , entonces , entonces 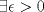 y y 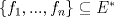 tales que tales que 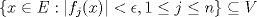 . Considere el operador lineal . Considere el operador lineal 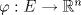 tal que tal que 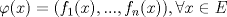 . Si . Si 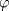 fuera inyectiva, entonces fuera inyectiva, entonces 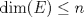 , lo que contradice la hipótesis. Luego , lo que contradice la hipótesis. Luego 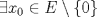 tal que tal que 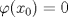 . Sea . Sea 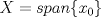 . Sea . Sea 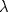 un escalar. Como un escalar. Como 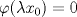 , entonces , entonces 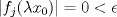 para todo para todo 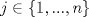 , i.e, , i.e, 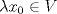 . Se sigue que . Se sigue que 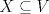 . Como . Como  si si 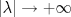 , entonces ninguna bola de radio finito contiene a , entonces ninguna bola de radio finito contiene a 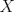 y se cumple lo mismo para y se cumple lo mismo para 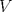 . .Lo último se obtiene por contrarrecíproco, en efecto, suponga que 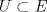 es abierto débil. Sea es abierto débil. Sea 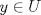 fijo. La traslación fijo. La traslación 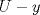 es una vecindad débil del cero y por el párrafo anterior es un conjunto no acotado. Por lo tanto es una vecindad débil del cero y por el párrafo anterior es un conjunto no acotado. Por lo tanto 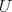 tampoco lo es. tampoco lo es. 
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 05:02 AM |







![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)




