Resolver Desigualdad - Foro fmat.cl

Resolver Desigualdad, Ayuda

Cristóbal Quezad... Cristóbal Quezada Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 4 2012, 02:52 PM Publicado: #1
Matemático Grupo: Usuario FMAT Mensajes: 68 Registrado: 17-November 11 Miembro Nº: 97.269 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	(ad+bc)(ac+bd)>cd(a+b)^2 Como se resuelve? Gracias -------------------- nadie es mejor que nadie, solo hay ****** más pencas que otros .- Arquímedes Oyarzún

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 4 2012, 02:59 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	hazla de atrás a adelante: desarrolla la desigualdad que tienes ahí y simplifica lo más que puedas (asumiendo que a,b,c,d>0), eso debería hacer que tengas mejores ideas -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

mercurial Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 4 2012, 03:39 PM Publicado: #3
Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 17-July 12 Miembro Nº: 109.090 Nacionalidad: Universidad: Sexo:	$TEX: desarrollando un poco<br />$$(ad+bc)\cdot(ac+bd)>cd(a+b)^2$$\\<br />$$a^2cd+d^2ab+c^2ab+b^2cd>a^2cd+2cdab+b^2cd$$\\<br />ahora nos queda por demostrar lo siguiente<br />$$ab\cdot \dfrac{(c^2+d^2)}{2}> cdab$$\\<br />lo cual es verdadero asumiendo que $a,b,c,d >0$ por $MA>MG$\\<br />$$\dfrac{c^2+d^2}{2}>cd \quad /\cdot ab$$<br />no se cambia el sentido ya q $a,b,c,d \in \mathbb{R}^+$\\ <br />$$ab\cdot \dfrac{c^2+d^2}{2}>cdab$$$ -------------------- $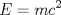TEX: $$E=mc^2$$$ $TEX: $$\mathfrak{POR}\ \mathfrak{EL}\ \mathfrak{DESARROLLO}\ \mathfrak{LIBRE}\ \mathfrak{DEL}\ \mathfrak{ESPIRITU} $$$

Cristóbal Quezad... Cristóbal Quezada Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 4 2012, 04:37 PM Publicado: #4
Matemático Grupo: Usuario FMAT Mensajes: 68 Registrado: 17-November 11 Miembro Nº: 97.269 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(mercurial @ Nov 4 2012, 03:39 PM) $TEX: desarrollando un poco<br />$$(ad+bc)\cdot(ac+bd)>cd(a+b)^2$$\\<br />$$a^2cd+d^2ab+c^2ab+b^2cd>a^2cd+2cdab+b^2cd$$\\<br />ahora nos queda por demostrar lo siguiente<br />$$ab\cdot \dfrac{(c^2+d^2)}{2}> cdab$$\\<br />lo cual es verdadero asumiendo que $a,b,c,d >0$ por $MA>MG$\\<br />$$\dfrac{c^2+d^2}{2}>cd \quad /\cdot ab$$<br />no se cambia el sentido ya q $a,b,c,d \in \mathbb{R}^+$\\ <br />$$ab\cdot \dfrac{c^2+d^2}{2}>cdab$$$ Gracias me habia dado cuenta, me queria pegar con una tabla cuando la hice, jajjjaa. Gracias de todos modos. -------------------- nadie es mejor que nadie, solo hay ****** más pencas que otros .- Arquímedes Oyarzún

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 4 2012, 04:50 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Cristóbal Quezada @ Nov 4 2012, 04:37 PM) Gracias me habia dado cuenta, me queria pegar con una tabla cuando la hice, jajjjaa. Gracias de todos modos. tú querías resolverlo como una inecuación!!!! hombre, tienes que saber lo que estás tratando de resolver! esa es una desigualdad que se cumple para todo a,b,c,d>0, no una inecuación. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 07:32 PM