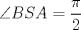|
|
|
|
|
|
|
  |
 Nov 10 2012, 07:21 AM Nov 10 2012, 07:21 AM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La única generalización que propuse fue cambiar "cuadrado" por "rombo" (tal y como habías mencionado). Al intentar el problema, quería intentar tres caminos (hasta que alguno me revelara una solución):
1.- Geometría euclidiana ("angle chasing", etc.). No estaba avanzando mucho... tratándose de un problema 2 de Cono Sur, supongo que tiene solución por este camino (sé que está la solución de Nabodorbuco, pero sólo la he "hojeado", sin detalle alguno). 2.- Inversión y esas cosas... No es mucho lo que sé de inversión, y prácticamente nada de otras técnicas que se puedan asociar a ella. El problema era con respecto a qué circunferencia(s) invertir. Mi primer intento fue c/r/a la circunferencia de diámetro AB, pero la recta CD no invertía en una figura "agradable". Mi segundo intento fue c/r/a la circunferencia circunscrita al cuadrado ABCD y todo se veía más "bonito", pero no fue suficiente. 3.- Geometría proyectiva Había visto la circunferencia que pasa por A, B, Q, R y O (precisamente donde quería ubicar S), el único problema para aplicar Pascal era que no recordaba la versión citada aquí (sólo recordaba la "habitual": a partir de seis puntos en una cónica se deducen tres puntos colineales). Sí tenía la sospecha sobre esta versión y que podía encontrarla en el libro de Fulton. Además, tenía los tres puntos colineales C, D y P. Para concluir, una vez demostrado por Pascal, la condición que P pertenezca al segmento AB también se puede liberar... por eso escribí "P un punto en la recta CD". Y bueno... todo eso pasó por mi mente cuando intenté resolver el problema... -------------------- |
|
|
|
 Nov 10 2012, 08:02 AM Nov 10 2012, 08:02 AM
Publicado:
#12
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Otra generalización: cambio el "rombo ABCD" por un "cuadrilátero ABCD (convexo o no) con diagonales perpendiculares". En este caso, sólo debo agregar que P no pertenezca a la recta AB, para que el triángulo ABP no sea degenerado (seguramente, se puede adaptar el problema para este caso).
De poder, creo que se puede continuar generalizando, pero no sé si tenga sentido. Al menos en la dirección que he adoptado para generalizar, usando Pascal, la mayor gracia del problema es precisamente "camuflar" dicho teorema. Si alguien quiere generalizar en otra dirección (¿Tiene sentido decir eso?)... estaremos leyendo. -------------------- |
|
|
|
 Nov 10 2012, 10:07 AM Nov 10 2012, 10:07 AM
Publicado:
#13
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Un camino que no usaste y que quizás abra la posibilidad a una nueva generalización, es usar una homotecia centrada en el circuncentro del cuadrado.
Mi primera solución al problema fue así, pero obviamente no es nada agradable como para publicarla xD -------------------- |
|
|
|
 Nov 10 2012, 10:18 AM Nov 10 2012, 10:18 AM
Publicado:
#14
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Dato Freak:
Salu2 =)!!! -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Dec 16 2012, 01:37 PM Dec 16 2012, 01:37 PM
Publicado:
#15
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
P6
![TEX: \[1<\frac{AB}{AC}<\frac{3}{2}\rightarrow AB>AC\]](/tex-image/b0f91f793f93c28bb4006a8c31e37b8a.png) ![TEX: \[\frac{MB}{AC}-\frac{NC}{AB}=1\]](/tex-image/958407f663a3237239aa9dd19cb44bbd.png) . De aqui en mas hacemos AC=1 entonces . De aqui en mas hacemos AC=1 entonces ![TEX: \[MB=1+\frac{NC}{AB}\]](/tex-image/c85ffdbbac412c59ff524cb0de2ce363.png) ,(1) ,(1)Con estos arreglos construimos el siguiente dibujo:  Ubicamos M,M' y N,N' en AB y AC respectivamente, cumpliendo con (1). Tenemos 2 triangulos 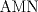 y y 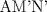 y sus y sus correspondientes circuncentros  y y 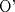 , luego , luego ![TEX: \[AN=1-NC\]](/tex-image/8cd3d40f08d7b037d6accd89c2373984.png) , , ![TEX: \[AN'=1-N'C\]](/tex-image/ada6011b8e99d77f5f62b3c12136892a.png) ![TEX: \[O'S=\frac{AN-AN'}{2}=\frac{N'C-NC}{2}\]](/tex-image/0526386e35977e2db55a5f79dfffb6d3.png) ![TEX: \[AM=(AB-1)-\frac{NC}{AB}\]](/tex-image/f09e29ac925c733b0f90a56351e85796.png) , , ![TEX: \[AM'=(AB-1)-\frac{N'C}{AB}\]](/tex-image/9e759ce61cebf5e02021012038a43193.png) ![TEX: \[O'R=\frac{AM-AM'}{2}=(\frac{N'C-NC}{2})\cdot \frac{1}{AB}\]](/tex-image/d65d5736d13821405f67ea01434ddb16.png) ![TEX: \[\frac{O'R}{O'S}= \frac{\frac{N'C-NC}{2}}{(\frac{N'C-NC}{2})\frac{1}{AB}}=\frac{1}{AB}=\frac{AC}{AB}\]](/tex-image/c464902fbd7191200b9338c23140fa35.png) ,(2) ,(2)ademas ![TEX: \[\angle RO'S=\angle CAB\]](/tex-image/ac0433931b91428a61a7129d581ea7fa.png) ,(3) (pues O'S//AC y O'R//AB) ,(3) (pues O'S//AC y O'R//AB)Entonces de (2) y (3) ![TEX: \[\Delta RO'S\sim \Delta CAB\]](/tex-image/17edf001ac357bfab42b34c7424b23d9.png) ,(4) ,(4)El cuadrilatero 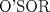 es ciclico y es ciclico y 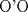 es diametro es diametrode la circunferencia que lo circunscribe. Por (4) el angulo que la altura del ![TEX: \[\Delta RO'S\]](/tex-image/b984f63b4d3128e5ef276a12f90783d0.png) , con pie en , con pie en 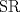 , forma , forma con el lado 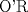 es igual a es igual a ![TEX: \[\angle HAC\]](/tex-image/79305ab80368e5a2476a670811333ba4.png) y por y por conjugado isogonal (ortoc.-circun.) podemos afirmar que ![TEX: \[\angle <br />HAC=\angle OO'S\]](/tex-image/106073d055ccd54a834e33c2ab7ff972.png) . Al ser . Al ser ![TEX: \[O'S\parallel AC\]](/tex-image/0b871517c7dc575280079b12aa29fdf6.png) tenemos tenemos que ![TEX: \[O'O\parallel AH\]](/tex-image/242f48d17e0e673d0d19b3871dbee610.png) Por 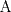 trazamos trazamos ![TEX: \[m\parallel BC\]](/tex-image/c0e48432f9173c6cc775b682fd536461.png) puede verse que puede verse que el otro punto (fijo), digamos 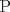 , distinto de , distinto de 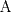 , , por el que deben pasar los circuncirculos de los triangulos ![TEX: \[AMN,AM'N',........\]](/tex-image/adb7fd668f8d646fd1706c4945aa8612.png) se debe encontrar sobre se debe encontrar sobre  de manera que 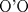 (su prolongacion) sea mediatriz de (su prolongacion) sea mediatriz de 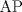 . El problema termina aqui pero podriamos calcular . El problema termina aqui pero podriamos calcular 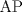 en funcion de los lados del en funcion de los lados del 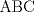 . .Si ![TEX: \[M\equiv A\]](/tex-image/536606517ecb647d98c76b8d33b93b92.png) existira un punto existira un punto ![TEX: \[N_{0}\]](/tex-image/c06d3df4724c91e4a1dbb70bf9720876.png) en en 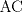 tal que tal que ![TEX: \[\frac{N_{o}C}{AB}= max= AB-1\rightarrow <br />N_{o}C=AB^2-AB\]](/tex-image/05cb5fe8d77018f89da585d2e43aa233.png) ,luego ,luego ![TEX: \[AN_{o}=1-N_{o}C=-AB^2+AB+1\]](/tex-image/0c6c6e43ed8f87e846122c8eb38f174e.png) Por la ciclicidad de ![TEX: \[AMNP,AM'N'P,.......\]](/tex-image/7318a62cde0c936d70b3f8eb8286cde1.png) podemos ver que podemos ver que ![TEX: \[\Delta MNP,\Delta M'N'P,.......\sim \Delta CBA\]](/tex-image/51b163d592fa3b1085c189b829d029c9.png) y como y como caso particular ![TEX: \[\Delta AN_{0}P\sim \Delta CBA\]](/tex-image/1c71145be93a5dbc78734697f75474c7.png) , luego , luego![TEX: \[\frac{AP}{AC}=\frac{AN_{0}}{BC}\rightarrow <br />AP=\frac{AN_{0}}{BC}=(-AB^2+AB+1)\frac{1}{BC}\]](/tex-image/e7bb261f664d76e6e19572673bc19492.png) -------------------------------------------------------- Dado el ABC, se puede encontrar P con un par de trazos tambien. -------------------- |
|
|
|
 Jan 27 2013, 12:31 AM Jan 27 2013, 12:31 AM
Publicado:
#16
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- Me voy, me jui.
|
|
|
|
 Jan 27 2013, 12:53 PM Jan 27 2013, 12:53 PM
Publicado:
#17
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Otra generalización: cambio el "rombo ABCD" por un "cuadrilátero ABCD (convexo o no) con diagonales perpendiculares". En este caso, sólo debo agregar que P no pertenezca a la recta AB, para que el triángulo ABP no sea degenerado (seguramente, se puede adaptar el problema para este caso). No es necesario que tenga diagonales perpendiculares! basta considerar el circuncírculo del triángulo formado por AB y el punto de intersección de dichas diagonales. Ahí de nuevo San Pascal salva el día como muestra el diagrama a continuación.  Sin_t_tulo.png ( 18.35k )
Número de descargas: 0
Sin_t_tulo.png ( 18.35k )
Número de descargas: 0Acá ABCD es un cuadrilátero cualquiera cuyas diagonales se cortan en E, luego se toma el circuncírculo de tr CDE y se elige el punto P en AB arbitrariamente. El resto lo sugiere el diagrama. Mensaje modificado por Kaissa el Jan 27 2013, 01:45 PM -------------------- |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:57 PM |














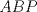 segun corresponda. Veamos que la altura desde
segun corresponda. Veamos que la altura desde 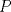 es paralela a
es paralela a 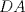 , por lo cual
, por lo cual 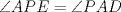 .
.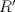 y
y  las respectivas prolongaciones de las alturas al tocar a los lados del cuadrado. Definamos como
las respectivas prolongaciones de las alturas al tocar a los lados del cuadrado. Definamos como 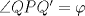 y
y 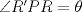 .
.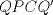 y
y 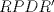 son cíclicos, por lo cual
son cíclicos, por lo cual 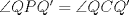 y
y 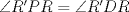 , entonces, por paralelismo
, entonces, por paralelismo 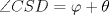 .
.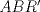 y
y 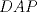 por criterio ALA, a saber, ángulo recto, lado del cuadrado y ángulo
por criterio ALA, a saber, ángulo recto, lado del cuadrado y ángulo 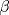 . Por lo cual
. Por lo cual 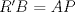 . Similarmente
. Similarmente 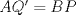 .
.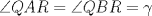 se tiene que
se tiene que 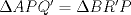 , por lo cual $\angle APQ'=\angle BR'P$ y entonces del $\Delta BR'P$ tenemos que
, por lo cual $\angle APQ'=\angle BR'P$ y entonces del $\Delta BR'P$ tenemos que 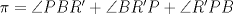
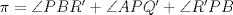
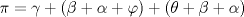
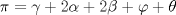
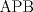 tenemos que
tenemos que 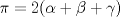 , por lo cual
, por lo cual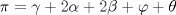
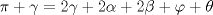
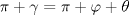
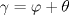
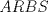 es cíclico, entonces como
es cíclico, entonces como 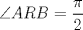 , se tiene que
, se tiene que