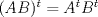 Control 1 / Primavera 2012, Matrices - Geometría |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Chile > Álgebra Lineal  |
 Sep 9 2012, 09:29 PM
Publicado:
#11
|
|
 Dios Matemático  Grupo: Usuario FMAT Mensajes: 277 Registrado: 15-October 08 Desde: Santiagopolis Miembro Nº: 36.209 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:   |
Una duda nada que ver, cómo le dicen sus pruebas, "certamenes", "pruebas", "interrogaciones"?
--------------------  |
 |
 
|
|
Sep 9 2012, 09:32 PM
Publicado:
#12
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-October 11 Miembro Nº: 95.494 Universidad:  |
CITA(Kamufler @ Sep 9 2012, 09:29 PM)  Una duda nada que ver, cómo le dicen sus pruebas, "certamenes", "pruebas", "interrogaciones"? ''control'' |
|
|
|
|
Sep 11 2012, 12:45 PM
Publicado:
#13
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 113 Registrado: 17-May 08 Miembro Nº: 23.481 Nacionalidad: Colegio/Liceo:  Universidad: Sexo: |
CITA(Shine @ Sep 3 2012, 10:12 AM) Semestre beta es el segundo semestre Semestre alfa es el primer semestre Según tengo entendido le dicen semestre beta, a cuando das el ramo en un semestre que no corresponde por malla.. Ej ahora por malla corresponde dar cálculo diferencial y álgebra lineal, entonces esos ramos son en semestre alfa, pero quienes lo den el próximo semestre lo darán en semestre beta |
|
|
|
|
Sep 22 2012, 04:33 PM
Publicado:
#14
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629 |
CITA(Uchiha Itachi @ Sep 1 2012, 06:25 PM) ![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaadofacaWGqbGaaGOmaaaaaeaacaWGHbGaaiykaiaabsfacaqG<br />% YbGaaeyyaiaabkgacaqGHbGaaeOAaiaabggacaqGUbGaaeizaiaab+<br />% gacaqGGaGaae4yaiaab+gacaqGUbGaaeiiaiaabcfacaqG6aaabaGa<br />% amiuamaaCaaaleqabaGaaGOmaaaakiabg2da9maabmaabaGaamysai<br />% abgkHiTiaad2eadaqadaqaaiaad2eadaahaaWcbeqaaiaadshaaaGc<br />% caWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislcaaIXaaaaO<br />% GaamytamaaCaaaleqabaGaamiDaaaaaOGaayjkaiaawMcaamaabmaa<br />% baGaamysaiabgkHiTiaad2eadaqadaqaaiaad2eadaahaaWcbeqaai<br />% aadshaaaGccaWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsisl<br />% caaIXaaaaOGaamytamaaCaaaleqabaGaamiDaaaaaOGaayjkaiaawM<br />% caaaqaaiabg2da9iaadMeacqGHsislcaaIYaWaaeWaaeaacaWGnbWa<br />% aeWaaeaacaWGnbWaaWbaaSqabeaacaWG0baaaOGaamytaaGaayjkai<br />% aawMcaamaaCaaaleqabaGaeyOeI0IaaGymaaaakiaad2eadaahaaWc<br />% beqaaiaadshaaaaakiaawIcacaGLPaaacqGHRaWkdaqadaqaaiaad2<br />% eadaqadaqaaiaad2eadaahaaWcbeqaaiaadshaaaGccaWGnbaacaGL<br />% OaGaayzkaaWaaWbaaSqabeaacqGHsislcaaIXaaaaOGaamytamaaCa<br />% aaleqabaGaamiDaaaaaOGaayjkaiaawMcaamaabmaabaGaamytamaa<br />% bmaabaGaamytamaaCaaaleqabaGaamiDaaaakiaad2eaaiaawIcaca<br />% GLPaaadaahaaWcbeqaaiabgkHiTiaaigdaaaGccaWGnbWaaWbaaSqa<br />% beaacaWG0baaaaGccaGLOaGaayzkaaaabaGaeyypa0Jaamysaiabgk<br />% HiTiaaikdadaqadaqaaiaad2eadaqadaqaaiaad2eadaahaaWcbeqa<br />% aiaadshaaaGccaWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsi<br />% slcaaIXaaaaOGaamytamaaCaaaleqabaGaamiDaaaaaOGaayjkaiaa<br />% wMcaaiabgUcaRiaad2eadaqadaqaaiaad2eadaahaaWcbeqaaiaads<br />% haaaGccaWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislcaaI<br />% XaaaaOWaaeWaaeaacaWGnbWaaWbaaSqabeaacaWG0baaaOGaamytaa<br />% GaayjkaiaawMcaamaabmaabaGaamytamaaCaaaleqabaGaamiDaaaa<br />% kiaad2eaaiaawIcacaGLPaaadaahaaWcbeqaaiabgkHiTiaaigdaaa<br />% GccaWGnbWaaWbaaSqabeaacaWG0baaaaGcbaGaeyypa0Jaamysaiab<br />% gkHiTiaaikdadaqadaqaaiaad2eadaqadaqaaiaad2eadaahaaWcbe<br />% qaaiaadshaaaGccaWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGH<br />% sislcaaIXaaaaOGaamytamaaCaaaleqabaGaamiDaaaaaOGaayjkai<br />% aawMcaaiabgUcaRiaad2eadaqadaqaaiaad2eadaahaaWcbeqaaiaa<br />% dshaaaGccaWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislca<br />% aIXaaaaOGaamytamaaCaaaleqabaGaamiDaaaaaOqaaiabg2da9iaa<br />% dMeacqGHsisldaqadaqaaiaad2eadaqadaqaaiaad2eadaahaaWcbe<br />% qaaiaadshaaaGccaWGnbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGH<br />% sislcaaIXaaaaOGaamytamaaCaaaleqabaGaamiDaaaaaOGaayjkai<br />% aawMcaaiabg2da9iaadcfaaeaaaeaacqGHshI3caWGqbWaaWbaaSqa<br />% beaacaaIYaaaaOGaeyypa0JaamiuaaqaaaqaaiaabMfacaqGGaGaae<br />% yyaiaabccacaqGZbGaaeyDaiaabccacaqG2bGaaeyzaiaabQhacaqG<br />% 6aGaaeiiaiaadcfacaWGnbGaeyypa0ZaaiWaaeaacaWGjbGaeyOeI0<br />% IaamytamaabmaabaGaamytamaaCaaaleqabaGaamiDaaaakiaad2ea<br />% aiaawIcacaGLPaaadaahaaWcbeqaaiabgkHiTiaaigdaaaGccaWGnb<br />% WaaWbaaSqabeaacaWG0baaaaGccaGL7bGaayzFaaGaamytaiabg2da<br />% 9iaad2eacqGHsislcaWGnbWaaeWaaeaacaWGnbWaaWbaaSqabeaaca<br />% WG0baaaOGaamytaaGaayjkaiaawMcaamaaCaaaleqabaGaeyOeI0Ia<br />% aGymaaaakiaad2eadaahaaWcbeqaaiaadshaaaGccaWGnbGaeyypa0<br />% JaamytaiabgkHiTiaad2eacqGH9aqpcaaIWaaabaaabaGaeyO0H4Ta<br />% amiuaiaad2eacqGH9aqpcaaIWaaabaaabaGaamOyaiaacMcacaqGGa<br />% WaaeWaaeaacaWGnbWaaWbaaSqabeaacaWG0baaaOGaamytaaGaayjk<br />% aiaawMcaamaaCaaaleqabaGaamiDaaaakiabg2da9iaad2eadaahaa<br />% WcbeqaaiaadshaaaGccaWGnbGaaeiiaiaabYcacaqGGaGaaeiBaiaa<br />% bwhacaqGLbGaae4zaiaab+gacaqGGaGaamytamaaCaaaleqabaGaam<br />% iDaaaakiaad2eacaqGGaGaaeyzaiaabohacaqGGaGaae4CaiaabMga<br />% caqGTbGaaeyzaiaabshacaqGYbGaaeyAaiaabogacaqGHbGaaeOlaa<br />% qaaiabgkziUkaadcfadaahaaWcbeqaaiaadshaaaGccqGH9aqpdaqa<br />% daqaaiaadMeacqGHsislcaWGnbWaaeWaaeaacaWGnbWaaWbaaSqabe<br />% aacaWG0baaaOGaamytaaGaayjkaiaawMcaamaaCaaaleqabaGaeyOe<br />% I0IaaGymaaaakiaad2eadaahaaWcbeqaaiaadshaaaaakiaawIcaca<br />% GLPaaadaahaaWcbeqaaiaadshaaaGccqGH9aqpcaWGjbGaeyOeI0Ya<br />% aeWaaeaacaWGnbWaaeWaaeaacaWGnbWaaWbaaSqabeaacaWG0baaaO<br />% GaamytaaGaayjkaiaawMcaamaaCaaaleqabaGaeyOeI0IaaGymaaaa<br />% kiaad2eadaahaaWcbeqaaiaadshaaaaakiaawIcacaGLPaaadaahaa<br />% WcbeqaaiaadshaaaGccqGH9aqpcaWGjbGaeyOeI0Iaamytamaadmaa<br />% baWaaeWaaeaacaWGnbWaaWbaaSqabeaacaWG0baaaOGaamytaaGaay<br />% jkaiaawMcaamaaCaaaleqabaGaeyOeI0IaaGymaaaaaOGaay5waiaa<br />% w2faamaaCaaaleqabaGaamiDaaaakiaad2eadaahaaWcbeqaaiaads<br />% haaaaakeaacqGH9aqpcaWGjbGaeyOeI0IaamytamaabmaabaGaamyt<br />% amaaCaaaleqabaGaamiDaaaakiaad2eaaiaawIcacaGLPaaadaahaa<br />% WcbeqaaiabgkHiTiaaigdaaaGccaWGnbWaaWbaaSqabeaacaWG0baa<br />% aOGaeyypa0JaamiuaaqaaaqaaiaabYeacaqG1bGaaeyzaiaabEgaca<br />% qGVbGaaeilaiaabccacaqGqbGaaeiiaiaabwgacaqGZbGaaeiiaiaa<br />% bohacaqGPbGaaeyBaiaabwgacaqG0bGaaeOCaiaabMgacaqGJbGaae<br />% yyaiaab6caaaaa!7CF7!<br />\[<br />\begin{gathered}<br /> \boxed{SP2} \hfill \\<br /> a){\text{Trabajando con P:}} \hfill \\<br /> P^2 = \left( {I - M\left( {M^t M} \right)^{ - 1} M^t } \right)\left( {I - M\left( {M^t M} \right)^{ - 1} M^t } \right) \hfill \\<br /> = I - 2\left( {M\left( {M^t M} \right)^{ - 1} M^t } \right) + \left( {M\left( {M^t M} \right)^{ - 1} M^t } \right)\left( {M\left( {M^t M} \right)^{ - 1} M^t } \right) \hfill \\<br /> = I - 2\left( {M\left( {M^t M} \right)^{ - 1} M^t } \right) + M\left( {M^t M} \right)^{ - 1} \left( {M^t M} \right)\left( {M^t M} \right)^{ - 1} M^t \hfill \\<br /> = I - 2\left( {M\left( {M^t M} \right)^{ - 1} M^t } \right) + M\left( {M^t M} \right)^{ - 1} M^t \hfill \\<br /> = I - \left( {M\left( {M^t M} \right)^{ - 1} M^t } \right) = P \hfill \\<br /> \hfill \\<br /> \Rightarrow P^2 = P \hfill \\<br /> \hfill \\<br /> {\text{Y a su vez: }}PM = \left\{ {I - M\left( {M^t M} \right)^{ - 1} M^t } \right\}M = M - M\left( {M^t M} \right)^{ - 1} M^t M = M - M = 0 \hfill \\<br /> \hfill \\<br /> \Rightarrow PM = 0 \hfill \\<br /> \hfill \\<br /> b){\text{ }}\left( {M^t M} \right)^t = M^t M{\text{ }}{\text{, luego }}M^t M{\text{ es simetrica}}{\text{.}} \hfill \\<br /> \to P^t = \left( {I - M\left( {M^t M} \right)^{ - 1} M^t } \right)^t = I - \left( {M\left( {M^t M} \right)^{ - 1} M^t } \right)^t = I - M\left[ {\left( {M^t M} \right)^{ - 1} } \right]^t M^t \hfill \\<br /> = I - M\left( {M^t M} \right)^{ - 1} M^t = P \hfill \\<br /> \hfill \\<br /> {\text{Luego}}{\text{, P es simetrica}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](/tex-image/70c4a02a9bde86d84057570f000711fa.png) 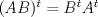de que manera transpusiste?? se supone que  y yo veo que haces 
|
|
|
|
|
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 05:27 PM |
