|
|
|
|
|
|
|
  |
 Sep 29 2012, 10:13 PM Sep 29 2012, 10:13 PM
Publicado:
#201
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Sep 30 2012, 04:53 PM Sep 30 2012, 04:53 PM
Publicado:
#202
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Propongo que proponga Marchiant Zotelo.
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Sep 30 2012, 06:28 PM Sep 30 2012, 06:28 PM
Publicado:
#203
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 206 Registrado: 25-January 11 Miembro Nº: 83.389 |
Esas son todas las soluciones,
http://www.wolframalpha.com/input/?i=k%5E2-7k%3Dn%5E2 Que proponga Marchiant Zotelo. |
|
|
|
 Oct 1 2012, 01:49 PM Oct 1 2012, 01:49 PM
Publicado:
#204
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ok, como no fue resuelto completamente, me veo en la obligación quizás de dar unos hint`s para que alguien lo resuelva, acá va:
Hint 1: Mega Hint 2 Salu2 Mensaje modificado por Seba² el Oct 1 2012, 01:59 PM -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Oct 1 2012, 02:58 PM Oct 1 2012, 02:58 PM
Publicado:
#205
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
@Seba:
Marchiant Zotelo dio todas las soluciones no-negativas. Es claro que con su primer argumento se puede determinar la única solución negativa (k=-9). -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Oct 1 2012, 04:36 PM Oct 1 2012, 04:36 PM
Publicado:
#206
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 19 Registrado: 28-March 12 Miembro Nº: 103.252 |
Falta otra solución, además del 0, el 7 y 16; Notar que k es entero (positivo o negativo)  Ok, como no fue resuelto completamente, me veo en la obligación.... Ok, señor obligado. No quiero proponer el siguiente. Adiós. PD: Que proponga el que se vea obligado a hacerlo. |
|
|
|
 Oct 1 2012, 07:18 PM Oct 1 2012, 07:18 PM
Publicado:
#207
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Primera cosa, a mi no me importa si se lo toman a mal, yo solo lo digo con todo el respeto y la buena onda...
Segunda cosa, yo puse ese Hint, para que la gente vea quizás un argumento simple(No digo que el tuyo sea más complejo), que sirve arto en ese estilo de problemas. Salu2!!! Mensaje modificado por Seba² el Oct 1 2012, 07:56 PM -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Oct 1 2012, 10:24 PM Oct 1 2012, 10:24 PM
Publicado:
#208
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 206 Registrado: 25-January 11 Miembro Nº: 83.389 |
Dada la situación, propongo:
Encuentre todas las parejas de enteros positivos ![TEX: \[(p, k)\]](/tex-image/cc6778d4aa45d6627054626893be7e65.png) para las cuales para las cuales ![TEX: \[p; (p + 2); (p + 2^k);(p + 2^k + 2) \]](/tex-image/1fce7dfef122d27f8b1fdacaa29ccfe8.png) son todos números primos. son todos números primos. |
|
|
|
 Oct 2 2012, 12:41 PM Oct 2 2012, 12:41 PM
Publicado:
#209
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Si p=2,3 la única solución es p=3, k=1.
Si p>3, entonces el análisis va así: p=3K-1 (pues p y p+2 son primos) p+2^k=3Q-1 (por la misma razón) sustituyendo tenemos 2^k=3(K-Q) así que K=Q, lo cual es imposible porque 2^k>0. Finalmente la única solución es (3,1) Si ta malo, bórrenlo. Si ta weno, propongan uds. Mensaje modificado por Kaissa el Oct 2 2012, 01:41 PM -------------------- |
|
|
|
 Oct 2 2012, 01:29 PM Oct 2 2012, 01:29 PM
Publicado:
#210
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 233 Registrado: 21-February 12 Desde: Cerro Navia, Santiago - Valparaíso Miembro Nº: 101.376 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
p=3K-1 (pues p y p+2 son primos) p+2^k=3Q-1 (por la misma razón) sustituyendo tenemos 2^k=3(K-Q) así que K=Q, lo cual es imposible porque 2^k>0. Finalmente no hay soluciones. Si ta malo, bórrenlo. Si ta weno, propongan uds. Está malo, pues el par (3,1) cumple lo pedido. --------------------  |
|
|
|
  |
3 usuario(s) está(n) leyendo esta discusión (3 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:25 PM |










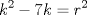
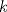 también debe ser cuadrado perfecto, y así obtienen una ecuación fácil de resolver
también debe ser cuadrado perfecto, y así obtienen una ecuación fácil de resolver

