|
|
|
|
|
|
|
  |
 Jun 2 2012, 11:59 PM Jun 2 2012, 11:59 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 17-April 12 Miembro Nº: 104.419 |
Maximo y mínimo de una función racional
Hola, me gustaria me pudiesen ayudar con 2 problemas, lo que pasa es que tengo una guía de maximo y minimo de funciones y cuando llegué a las racionales no supe que hacer, la guia es solo de ejercitacion no evaluada, Porfavor ayudenme es que no le entiendo mucho a mi profesor y me tengo clases con él hasta el lunes, pero yo quiero llegar preparado a esa clase: 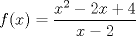 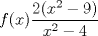 Dice determinar máximo y mínimo, los intervalos en donde la aplicación crece o decrece y la gráfica, pero con lo que me puedan ayudar estaré agradecido, ojala puedan ayudarme. Gracias. Mensaje modificado por Creeper el Jun 3 2012, 12:06 AM |
|
|
|
 Jun 3 2012, 12:10 AM Jun 3 2012, 12:10 AM
Publicado:
#2
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 85 Registrado: 11-August 08 Miembro Nº: 31.944 Nacionalidad:  Universidad:  Sexo:  |
para saber donde crece o decrece debes derivar y con los puntos criticos determinas
luego para hacer una grafica mas decente, encuentra la segunda derivada y sus puntos criticos con eso tendras un bosquejo mas claro de como es la grafica |
|
|
|
 Jun 3 2012, 12:13 AM Jun 3 2012, 12:13 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad:  Sexo:  |
recuerda que la derivada de una funcion en un punto es la pendiente de la recta tangente a la curva en ese punto
si la recta es horizontal, puede haber maximo o minimo en dicho punto, por lo que como es horizontal su pendiente es cero, es decir, su derivada en dicho punto es cero. la mecanica es derivar una vez, igualar a cero, encuentras los ceros de la derivada y tienes los puntos criticos para saber si es minimo o maximo tienes criterios de derivadas primeras por cambio de signos o por la segunda derivada.... |
|
|
|
 Jun 3 2012, 12:14 AM Jun 3 2012, 12:14 AM
Publicado:
#4
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 17-April 12 Miembro Nº: 104.419 |
para saber donde crece o decrece debes derivar y con los puntos criticos determinas luego para hacer una grafica mas decente, encuentra la segunda derivada y sus puntos criticos con eso tendras un bosquejo mas claro de como es la grafica Mira, gracias por querer ayudarme, en el primer ejercicio encontre los 2 puntos criticos de la funcion (4 y 0) pero luego no se como proseguir. |
|
|
|
 Jun 3 2012, 12:40 AM Jun 3 2012, 12:40 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad:  Sexo:  |
ojo que los puntos criticos deben ser de la PRIMERA DERIVADA
puedes postear tu primera derivada? |
|
|
|
 Jun 3 2012, 01:03 AM Jun 3 2012, 01:03 AM
Publicado:
#6
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 17-April 12 Miembro Nº: 104.419 |
ojo que los puntos criticos deben ser de la PRIMERA DERIVADA puedes postear tu primera derivada? Hola, gracias, mira, en esto voy: 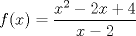 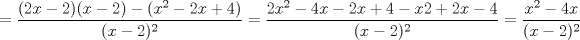 despues igualé la funcion a 0: 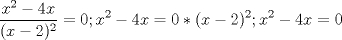 y me quedó una ecuacion, sus ceros me dieron como resultado: 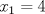 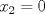 Hasta esa parte llego, lo hice guiándome con un video en youtube Mensaje modificado por Creeper el Jun 3 2012, 01:06 AM |
|
|
|
 Jun 3 2012, 01:11 AM Jun 3 2012, 01:11 AM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 608 Registrado: 18-April 10 Desde: Santiasco Miembro Nº: 69.076 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Mira acá
En resumen es: los puntos críticos los evalúas en la segunda derivada y; si te da < 0 es máximo, > 0 es mínimo -------------------- |
|
|
|
 Jun 3 2012, 01:13 AM Jun 3 2012, 01:13 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad:  Sexo:  |
yapo, ahora analicemos lo siguiente:
CRITERIO DE LA PRIMERA DERIVADA Si un punto critico hace cero la primera derivada, entonces quiere decir que en dicho punto la tangente es horizontal. por lo tanto, si la tangente se mueve de izquierda a derecha, DEBERIA haber un cambio de signo en la derivada evaluada en dicho punto. toma uno de tus puntos criticos, por ejemplo el x=4. Si en x=4 hay un maximo entonces quiere decir que a la izquierda del x=4 la derivada era positiva y a la derecha del x=4 la derivada es negativa... porque? imaginate la recta tangente recorriendo la grafica de izquierda a derecha... Entonces: toma un valor a izquierda y otro a derecha del x=4 y reemplaza en la primera derivada: Si tienes un cambio de signo de positivo a negativo entonces es maximo Si tienes un cambio de signo de negativo a positivo entonces es minimo. PD: este criterio no me gusta mucho porque debes tomar un valor muy cercano al cero...prefiero el de la segunda derivada que es mas FACIL Y DIRECTO. |
|
|
|
 Jun 3 2012, 01:44 AM Jun 3 2012, 01:44 AM
Publicado:
#9
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 85 Registrado: 11-August 08 Miembro Nº: 31.944 Nacionalidad:  Universidad:  Sexo:  |
lo hice, toy recagao de sueño y haciendo un informe, asi que puede que se me haya ido algo o me equivoque en algo, revisa bien
para el primer ejercicio, los puntos criticos son: x=0 y x=4 en donde la funcion crece entre (-infinito a 0) union (4, +infinito) y decrece en (0,4) aparte debes visualizar que en x=2 hay una asintota vertical por lo tanto en el punto (0,-2) tienes un maximo relativo y en (4,6) tienes un minimo relativo ahora si vuelves a derivar veras que en x=2 cambia la concavidad de la funcion por lo tanto: en (2,+ infinito) es concava hacia arriba y en (-infinito,2) es concava hacia abajo ahora para el segundo el punto critico seria x=0 hay asintotas verticales en x=-2 y x=2 por lo tanto la funcion crece en (0,+infinito) y decrece en -infinito, 0) la segunda derivada da como puntos criticos x=-2 y x=2 entonces la funcion es concava hacia arriba en (-2,2) y concava hacia abajo en (-infinito, -2) y (2, +infinito) aparte la funcion tiene asintota horizontal en y=2 ojala que todo lo que puse este bueno, que alguien corroborre, a esta hora no me quedan neuronas :xd salu2 |
|
|
|
 Jun 3 2012, 01:46 AM Jun 3 2012, 01:46 AM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad:  Sexo:  |
Siempre digo:
"El café, además de ser antioxidante, REGENERA Neuronas de manera exponencial entre las 01am y las 06am" |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:37 PM |