|
|
|
|
|
|
|
  |
 Apr 27 2012, 01:46 PM Apr 27 2012, 01:46 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
.
Mensaje modificado por El Geek el Sep 20 2014, 03:08 PM -------------------- Me voy, me jui.
|
|
|
|
 Apr 28 2012, 12:43 AM Apr 28 2012, 12:43 AM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 340 Registrado: 18-May 06 Desde: ..la eskinaa...!!! Miembro Nº: 1.125 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solución Problema 2:
b. Sea A un conjunto finito, probemos que toda sucesión en él tiene una subsucesión convergente, esto garantizará la compacidad de A. Sea 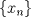 sucesión en A. Como la sucesión sucesión en A. Como la sucesión 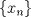 es infinita y A finito, existirá al menos un es infinita y A finito, existirá al menos un  que se repetirá infinitas veces en que se repetirá infinitas veces en 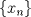 , o sea existe una subsucesión , o sea existe una subsucesión 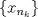 tal que tal que 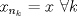 , la cual por tanto es convergente de límite , la cual por tanto es convergente de límite  . . De lo anterior concluimos que A es compacto. a. Como  es finito, entonces es compacto, luego es cerrado, por tanto es finito, entonces es compacto, luego es cerrado, por tanto 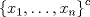 es abierto, de donde obtenemos que es abierto, de donde obtenemos que 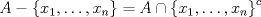 es abierto al ser intersección finita de abiertos. es abierto al ser intersección finita de abiertos.
|
|
|
|
 Apr 28 2012, 08:59 AM Apr 28 2012, 08:59 AM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No sé quien está mal, tu redacción o yo. Por otra parte, te falta en el 2 demostrar que está acotado.
Anímense con los problemas fuertes del asunto -------------------- Me voy, me jui.
|
|
|
|
 Apr 28 2012, 10:09 AM Apr 28 2012, 10:09 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La demostración de oliver está correcta, agrego que la definición estilo Weierstrass de compacidad (con sucesiones) es independiente de la de Heine-Borel, aunque claramente en espacios métricos son equivalentes.
-------------------- |
|
|
|
 Apr 29 2012, 09:06 AM Apr 29 2012, 09:06 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
¿Ah entonces está bien que haya escrito "entonces es compacto" cuándo eso es lo que se quiere demostrar?
-------------------- Me voy, me jui.
|
|
|
|
 Apr 29 2012, 09:09 AM Apr 29 2012, 09:09 AM
Publicado:
#6
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Es porque utilizó la parte b) para demostrar la a).
|
|
|
|
 Apr 29 2012, 01:44 PM Apr 29 2012, 01:44 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Bah, no había leido que primero solucionó b y luego a. Con razón me hacía corto circuito, gracias.
-------------------- Me voy, me jui.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 05:03 AM |










