Desigualdad de Nesbit - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Desigualdades > Problemas Resueltos

3 Páginas:

1 2 3 >

Reply to this topic

Start new topic

Desigualdad de Nesbit, 7 soluciones...Resuelto por TheLord, CAPQ, tebas, caf_tito, PaulRS, Re

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 6 2007, 03:03 PM Publicado: #1
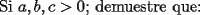Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: 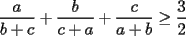Sexo:	$TEX: Si $a,b,c>0$; demuestre que:$ $TEX: $\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge \dfrac{3}{2}$$ Saludos

The Lord Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 6 2007, 04:53 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Esta desigualdad me trae lindos recuerdos, porq fue una de las primeras que hice $TEX: \noindent Por Cauchy sabemos que:\\<br />$((a+b)+(b+c)+(a+c))(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c})\ge 9$\\<br />\\<br />$(a+b+c)(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c})\ge\dfrac{9}{2}$\\<br />\\<br />$\dfrac{a+b+c}{a+b}+\dfrac{a+b+c}{b+c}+\dfrac{a+b+c}{a+c}\ge\dfrac{9}{2}$\\<br />\\<br />$\dfrac{a}{b+c}+1+\dfrac{b}{a+c}+1+\dfrac{c}{a+b}+1\ge\dfrac{9}{2}$\\<br />\\<br />$\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\ge\dfrac{3}{2}$\\<br />Asi probando lo pedido$ Saludos

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 6 2007, 04:59 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Muy bien, llevamos una solución correcta utilizando Cauchy-Shwarz faltan 3 mas (talvez darse unas vueltas por el sector contenidos en un par de capítulos mas no estaria mal)

CAPQ Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 10 2007, 09:03 AM Publicado: #4
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 22 Registrado: 22-June 07 Desde: Lima - Perú Miembro Nº: 6.962 Nacionalidad: Sexo:	$TEX: Aqui otra soluci\'on:\\<br />Sea\\<br />T = $\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}$\\\\<br />T +3 = $\dfrac{a}{b+c}+1+\dfrac{b}{a+c}+1+\dfrac{c}{a+b}+1$\\\\<br />T +3 = $\dfrac{a+b+c}{b+c}+\dfrac{a+b+c}{a+c}+\dfrac{a+b+c}{a+b}$\\\\<br />Luego: [media aritm\'etica] $\ge$ [media arm\'onica]\\\\<br />$\dfrac{\dfrac{a+b+c}{b+c}+\dfrac{a+b+c}{a+c}+\dfrac{a+b+c}{a+b}}{3}\ge\dfrac{3}{\dfrac{b+c}{a+b+c}+\dfrac{a+c}{a+b+c}+\dfrac{a+b}{a+b+c}}$\\\\<br />$\dfrac{T+3}{3}\ge\dfrac{3}{\dfrac{2(a+b+c)}{a+b+c}}$\\\\Por lo tanto: { } <br />$T\ge\dfrac{3}{2}$<br />$ Mensaje modificado por CAPQ el Jul 10 2007, 09:52 AM

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 10 2007, 03:49 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Correcta Saludos

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 18 2008, 02:09 PM Publicado: #6
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	CITA(Luffy @ Apr 6 2007, 06:03 PM) $TEX: Si $a,b,c>0$; demuestre que:$ $TEX: $\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge \dfrac{3}{2}$$ Saludos $TEX: \noindent Sin perdida de generalidad asumamos $a\ge b\ge c\ge 0$\\ $\implies a+b\ge a+c\ge b+c\therefore \dfrac{a}{b+c}\ge \dfrac{b}{a+c}\ge \dfrac{c}{a+b}$\\ por Chebyshev\\ $\left( {b + c + a + c + a + b} \right)\sum\limits_{ciclica} {\dfrac{a}{{b + c}}}\ge 3\left( {a + b + c} \right)$\\ $\implies \sum\limits_{ciclica} {\dfrac{a}{{b + c}}} \ge \dfrac{3}{2}$$ --------------------

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 18 2008, 10:27 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(caf_tito @ Jan 18 2008, 05:09 PM) $TEX: \noindent Sin perdida de generalidad asumamos $a\ge b\ge c\ge 0$\\ $\implies a+b\ge a+c\ge b+c\therefore \dfrac{a}{b+c}\ge \dfrac{b}{a+c}\ge \dfrac{c}{a+b}$\\ por Chebyshev\\ $\left( {b + c + a + c + a + b} \right)\sum\limits_{ciclica} {\dfrac{a}{{b + c}}}\ge 3\left( {a + b + c} \right)$\\ $\implies \sum\limits_{ciclica} {\dfrac{a}{{b + c}}} \ge \dfrac{3}{2}$$ Perfecto, esta era otra de las soluciones que pedí en algún momento cuando inicié este tema Se agradece y sigue asi

tebas Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 3 2008, 04:06 PM Publicado: #8
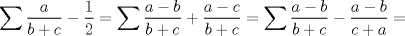Maestro Matemático Grupo: Usuario FMAT Mensajes: 85 Registrado: 9-January 08 Desde: Guatemala Miembro Nº: 14.478 Sexo:	No me acuerdo donde vi esta pero es interesante. 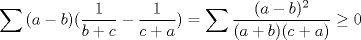$TEX: $\displaystyle \sum{\frac{a}{b+c}-\frac{1}{2}}=\sum{\frac{a-b}{b+c}+\frac{a-c}{b+c}}=\sum{\frac{a-b}{b+c}-\frac{a-b}{c+a}}=$$ $TEX: $\displaystyle\sum{(a-b)(\frac{1}{b+c}-\frac{1}{c+a})}=\sum{\frac{(a-b)^2}{(a+b)(c+a)}}\ge 0$$ y aqui hay otra con MA.GM Sean 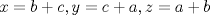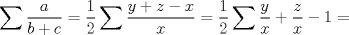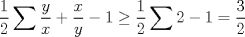$TEX: $x=b+c, y=c+a, z=a+b$$ $TEX: $\displaystyle\sum{\frac{a}{b+c}}=\frac{1}{2}\sum{\frac{y+z-x}{x}}=\frac{1}{2}\sum{\frac{y}{x}+\frac{z}{x}-1}=$$ $TEX: $\displaystyle\frac{1}{2}\sum{\frac{y}{x}+\frac{x}{y}-1}\ge\frac{1}{2}\sum{2-1}=\frac{3}{2}$$ Respueta al siguiente post: Editado. Que bonita la otra demostración. Mensaje modificado por tebas el Aug 5 2008, 11:01 PM

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2008, 07:46 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(tebas @ Aug 3 2008, 04:56 PM) No me acuerdo donde vi esta pero es interesante. 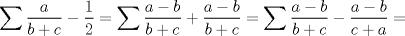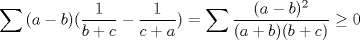$TEX: $\displaystyle \sum{\frac{a}{b+c}-\frac{1}{2}}=\sum{\frac{a-b}{b+c}+\frac{a-b}{b+c}}=\sum{\frac{a-b}{b+c}-\frac{a-b}{c+a}}=$$ $TEX: $\displaystyle\sum{(a-b)(\frac{1}{b+c}-\frac{1}{c+a})}=\sum{\frac{(a-b)^2}{(a+b)(b+c)}}\ge 0$$ y aqui hay otra con MA.GM Sean 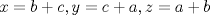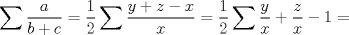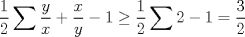$TEX: $x=b+c, y=c+a, z=a+b$$ $TEX: $\displaystyle\sum{\frac{a}{b+c}}=\frac{1}{2}\sum{\frac{y+z-x}{x}}=\frac{1}{2}\sum{\frac{y}{x}+\frac{z}{x}-1}=$$ $TEX: $\displaystyle\frac{1}{2}\sum{\frac{y}{x}+\frac{x}{y}-1}\ge\frac{1}{2}\sum{2-1}=\frac{3}{2}$$ Me parece que la primera desigualdad debiera desarrollarse de la siguiente manera: 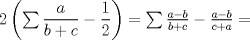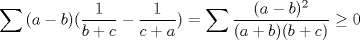$TEX: $2\left( \sum\dfrac{a}{b+c}-\dfrac{1}{2}\right) =\sum{\frac{a-b}{b+c}-\frac{a-b}{c+a}}=$$ $TEX: $\displaystyle\sum{(a-b)(\frac{1}{b+c}-\frac{1}{c+a})}=\sum{\frac{(a-b)^2}{(a+b)(b+c)}}\ge 0$$ Y la otra solución es correcta De hecho les anexo una adicional que encontré por ahí para los interesados: Sean 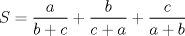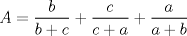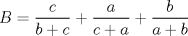$TEX: $S=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}$$ ; $TEX: $A=\dfrac{b}{b+c}+\dfrac{c}{c+a}+\dfrac{a}{a+b}$$ ; $TEX: $B=\dfrac{c}{b+c}+\dfrac{a}{c+a}+\dfrac{b}{a+b}$$ . $TEX: $A+S=\dfrac{a+b}{b+c}+\dfrac{b+c}{c+a}+\dfrac{c+a}{a+b}\ge 3\sqrt[3]{\dfrac{a+b}{b+c}\cdot \dfrac{b+c}{c+a}\cdot \dfrac{c+a}{a+b}}=3$$ $TEX: $B+S=\dfrac{c+a}{b+c}+\dfrac{a+b}{c+a}+\dfrac{b+c}{a+b}\ge 3\sqrt[3]{\dfrac{c+a}{b+c}\cdot \dfrac{a+b}{b+c}\cdot \dfrac{c+a}{a+b}}=3$$ $TEX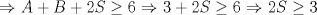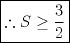: $A+B=\dfrac{b+c}{b+c}+\dfrac{c+a}{c+a}+\dfrac{a+b}{a+b}= 3$$ $TEX: $\Rightarrow$ $A+B+2S\ge 6$ $\Rightarrow$ $3+2S\ge 6$ $\Rightarrow$ $2S\ge 3$$ $TEX: $\boxed{\therefore S\ge \dfrac{3}{2}}$$ Saludos

PaulRS Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 5 2009, 05:19 PM Publicado: #10
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 156 Registrado: 11-June 07 Miembro Nº: 6.615 Nacionalidad: Sexo:	Por Cauchy-Schwarz: 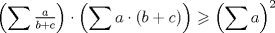$TEX: $$<br />\left( {\sum {\tfrac{a}<br />{{b + c}}} } \right) \cdot \left( {\sum {a \cdot \left( {b + c} \right)} } \right) \geqslant \left( {\sum a } \right)^2 <br />$$$ Ahora: 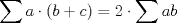$TEX: $$<br />\sum {a \cdot \left( {b + c} \right)} = 2 \cdot \sum {ab} <br />$$$ y luego: $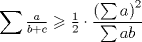TEX: $$<br />\sum {\tfrac{a}<br />{{b + c}}} \geqslant \tfrac{1}<br />{2} \cdot \frac{{\left( {\sum a } \right)^2 }}<br />{{\sum {ab} }}<br />$$$ Y como: $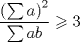TEX: $$<br />\frac{{\left( {\sum a } \right)^2 }}<br />{{\sum {ab} }} \geqslant 3<br />$$$ se sigue la desigualdad de Nesbit. Saludos -------------------- $TEX: $\sqrt[3]{\displaystyle\sum_{i=1}^n{i^{3\cdot{\sqrt[]{3}}-1}}}\approx{\displaystyle\sum_{i=1}^n{i^{\sqrt[]{3}-1}}}$$

« Posterior · Problemas Resueltos · Anterior »

3 Páginas:

1 2 3 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 10:02 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.