|
|
|
|
|
|
|
  |
 Mar 10 2012, 09:42 PM Mar 10 2012, 09:42 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
.
Mensaje modificado por El Geek el Sep 21 2014, 02:29 AM -------------------- Me voy, me jui.
|
|
|
|
 Mar 10 2012, 09:57 PM Mar 10 2012, 09:57 PM
Publicado:
#2
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Para el 6.a
![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqada<br />% qaamaalaaabaGaaGymaiabgUcaRiaadMgaaeaadaGcaaqaaiaaikda<br />% aSqabaaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaWGUbaaaOGaey<br />% ypa0ZaaeWaaeaadaWcaaqaaiaaigdaaeaadaGcaaqaaiaaikdaaSqa<br />% baaaaOGaey4kaSIaamyAaiabgwSixpaalaaabaGaaGymaaqaamaaka<br />% aabaGaaGOmaaWcbeaaaaaakiaawIcacaGLPaaadaahaaWcbeqaaiaa<br />% d6gaaaGccqGH9aqpdaqadaqaamaalaaabaWaaOaaaeaacaaIYaaale<br />% qaaaGcbaGaaGOmaaaacqGHRaWkcaWGPbWaaSaaaeaadaGcaaqaaiaa<br />% ikdaaSqabaaakeaacaaIYaaaaaGaayjkaiaawMcaamaaCaaaleqaba<br />% GaamOBaaaakiabg2da9maacmaabaGaam4yaiaadMgacaWGZbWaaeWa<br />% aeaadaWcaaqaaiabec8aWbqaaiaaisdaaaaacaGLOaGaayzkaaaaca<br />% GL7bGaayzFaaWaaWbaaSqabeaacaWGUbaaaOGaeyypa0Jaam4yaiaa<br />% dMgacaWGZbWaaeWaaeaadaWcaaqaaiaad6gacqGHflY1cqaHapaCae<br />% aacaaI0aaaaaGaayjkaiaawMcaaaqaaiabgkDiElaadIhadaWgaaWc<br />% baGaamOBaaqabaGccqGHRaWkcaWGPbGaamyEamaaBaaaleaacaWGUb<br />% aabeaakiabg2da9iaadogacaWGPbGaam4CamaabmaabaWaaSaaaeaa<br />% caWGUbGaeyyXICTaeqiWdahabaGaaGinaaaaaiaawIcacaGLPaaaae<br />% aaaeaacaqGmbGaaeyDaiaabwgacaqGNbGaae4BaiaabQdaaeaacaWG<br />% 4bWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaadMhadaWgaa<br />% WcbaGaamOBaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaad6gaaeqa<br />% aOGaamyEamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccqGH9a<br />% qpciGGJbGaai4BaiaacohadaqadaqaamaalaaabaWaaeWaaeaacaWG<br />% UbGaeyOeI0IaaGymaaGaayjkaiaawMcaaiabec8aWbqaaiaaisdaaa<br />% aacaGLOaGaayzkaaGaci4CaiaacMgacaGGUbWaaeWaaeaadaWcaaqa<br />% aiaad6gacqaHapaCaeaacaaI0aaaaaGaayjkaiaawMcaaiabgkHiTi<br />% GacogacaGGVbGaai4CamaabmaabaWaaSaaaeaacaWGUbGaeqiWdaha<br />% baGaaGinaaaaaiaawIcacaGLPaaaciGGZbGaaiyAaiaac6gadaqada<br />% qaamaalaaabaWaaeWaaeaacaWGUbGaeyOeI0IaaGymaaGaayjkaiaa<br />% wMcaaiabec8aWbqaaiaaisdaaaaacaGLOaGaayzkaaaabaGaamiEam<br />% aaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaWG5bWaaSbaaSqa<br />% aiaad6gaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaWGUbaabeaaki<br />% aadMhadaWgaaWcbaGaamOBaiabgkHiTiaaigdaaeqaaOGaeyypa0Ja<br />% ci4CaiaacMgacaGGUbWaaeWaaeaadaWcaaqaaiaad6gacqaHapaCae<br />% aacaaI0aaaaiabgkHiTmaalaaabaWaaeWaaeaacaWGUbGaeyOeI0Ia<br />% aGymaaGaayjkaiaawMcaaiabec8aWbqaaiaaisdaaaaacaGLOaGaay<br />% zkaaaabaGaamiEamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGc<br />% caWG5bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaamiEamaaBaaale<br />% aacaWGUbaabeaakiaadMhadaWgaaWcbaGaamOBaiabgkHiTiaaigda<br />% aeqaaOGaeyypa0Jaci4CaiaacMgacaGGUbWaaeWaaeaadaWcaaqaai<br />% abec8aWbqaaiaaisdaaaaacaGLOaGaayzkaaaabaGaamiEamaaBaaa<br />% leaacaWGUbGaeyOeI0IaaGymaaqabaGccaWG5bWaaSbaaSqaaiaad6<br />% gaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaWGUbaabeaakiaadMha<br />% daWgaaWcbaGaamOBaiabgkHiTiaaigdaaeqaaOGaeyypa0ZaaSaaae<br />% aadaGcaaqaaiaaikdaaSqabaaakeaacaaIYaaaaaaaaa!F5CF!<br />\[<br />\begin{gathered}<br /> \left( {\frac{{1 + i}}<br />{{\sqrt 2 }}} \right)^n = \left( {\frac{1}<br />{{\sqrt 2 }} + i \cdot \frac{1}<br />{{\sqrt 2 }}} \right)^n = \left( {\frac{{\sqrt 2 }}<br />{2} + i\frac{{\sqrt 2 }}<br />{2}} \right)^n = \left\{ {cis\left( {\frac{\pi }<br />{4}} \right)} \right\}^n = cis\left( {\frac{{n \cdot \pi }}<br />{4}} \right) \hfill \\<br /> \Rightarrow x_n + iy_n = cis\left( {\frac{{n \cdot \pi }}<br />{4}} \right) \hfill \\<br /> \hfill \\<br /> {\text{Luego:}} \hfill \\<br /> x_{n - 1} y_n - x_n y_{n - 1} = \cos \left( {\frac{{\left( {n - 1} \right)\pi }}<br />{4}} \right)\sin \left( {\frac{{n\pi }}<br />{4}} \right) - \cos \left( {\frac{{n\pi }}<br />{4}} \right)\sin \left( {\frac{{\left( {n - 1} \right)\pi }}<br />{4}} \right) \hfill \\<br /> x_{n - 1} y_n - x_n y_{n - 1} = \sin \left( {\frac{{n\pi }}<br />{4} - \frac{{\left( {n - 1} \right)\pi }}<br />{4}} \right) \hfill \\<br /> x_{n - 1} y_n - x_n y_{n - 1} = \sin \left( {\frac{\pi }<br />{4}} \right) \hfill \\<br /> x_{n - 1} y_n - x_n y_{n - 1} = \frac{{\sqrt 2 }}<br />{2} \hfill \\ <br />\end{gathered} <br />\]](/tex-image/15abe6d5c2c2b9f239a2327e32180793.png) -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
 Mar 10 2012, 10:04 PM Mar 10 2012, 10:04 PM
Publicado:
#3
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Para el 6.b
![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGdb<br />% Gaae4Baiaab6gacaqGZbGaaeyAaiaabsgacaqGLbGaaeOCaiaabwga<br />% caqGTbGaae4BaiaabohacaqGGaGaamOEaiabg2da9iaadggacqGHRa<br />% WkcaWGIbGaamyAaiabgIGiolablkqiJkabgkHiTmaacmaabaGaaGym<br />% aaGaay5Eaiaaw2haaiaabYcacaqGGaGaaeiBaiaabwhacaqGLbGaae<br />% 4zaiaab+gacaqG6aaabaWaaSaaaeaacaWG6bGaey4kaSIaaGymaaqa<br />% aiaadQhacqGHsislcaaIXaaaaiabg2da9maalaaabaGaamyyaiabgU<br />% caRiaadkgacaWGPbGaey4kaSIaaGymaaqaaiaadggacqGHRaWkcaWG<br />% IbGaamyAaiabgkHiTiaaigdaaaGaeyypa0ZaaSaaaeaadaqadaqaai<br />% aadggacqGHRaWkcaaIXaaacaGLOaGaayzkaaGaey4kaSIaamOyaiaa<br />% dMgaaeaadaqadaqaaiaadggacqGHsislcaaIXaaacaGLOaGaayzkaa<br />% Gaey4kaSIaamOyaiaadMgaaaGaeyypa0ZaaSaaaeaadaGadaqaamaa<br />% bmaabaGaamyyaiabgUcaRiaaigdaaiaawIcacaGLPaaacqGHRaWkca<br />% WGIbGaamyAaaGaay5Eaiaaw2haamaacmaabaWaaeWaaeaacaWGHbGa<br />% eyOeI0IaaGymaaGaayjkaiaawMcaaiabgkHiTiaadkgacaWGPbaaca<br />% GL7bGaayzFaaaabaWaaiWaaeaadaqadaqaaiaadggacqGHsislcaaI<br />% XaaacaGLOaGaayzkaaGaey4kaSIaamOyaiaadMgaaiaawUhacaGL9b<br />% aadaGadaqaamaabmaabaGaamyyaiabgkHiTiaaigdaaiaawIcacaGL<br />% PaaacqGHsislcaWGIbGaamyAaaGaay5Eaiaaw2haaaaaaeaadaWcaa<br />% qaaiaadQhacqGHRaWkcaaIXaaabaGaamOEaiabgkHiTiaaigdaaaGa<br />% eyypa0ZaaSaaaeaacaWGHbWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0<br />% IaaGymaiabgkHiTiaadkgacaWGPbWaaeWaaeaacaWGHbGaey4kaSIa<br />% aGymaaGaayjkaiaawMcaaiabgUcaRiaadkgacaWGPbWaaeWaaeaaca<br />% WGHbGaeyOeI0IaaGymaaGaayjkaiaawMcaaiabgUcaRiaadkgadaah<br />% aaWcbeqaaiaaikdaaaaakeaadaqadaqaaiaadggacqGHsislcaaIXa<br />% aacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOy<br />% amaaCaaaleqabaGaaGOmaaaaaaaakeaadaWcaaqaaiaadQhacqGHRa<br />% WkcaaIXaaabaGaamOEaiabgkHiTiaaigdaaaGaeyypa0ZaaSaaaeaa<br />% caWGHbWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOyamaaCaaale<br />% qabaGaaGOmaaaakiabgkHiTiaaigdacqGHRaWkcaWGIbGaamyAamaa<br />% bmaabaGaamyyaiabgkHiTiaaigdacqGHsislcaWGHbGaeyOeI0IaaG<br />% ymaaGaayjkaiaawMcaaaqaamaabmaabaGaamyyaiabgkHiTiaaigda<br />% aiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGIb<br />% WaaWbaaSqabeaacaaIYaaaaaaaaOqaamaalaaabaGaamOEaiabgUca<br />% RiaaigdaaeaacaWG6bGaeyOeI0IaaGymaaaacqGH9aqpdaWcaaqaai<br />% aadggadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGIbWaaWbaaSqa<br />% beaacaaIYaaaaOGaeyOeI0IaaGymaiabgkHiTiaaikdacaWGIbGaam<br />% yAaaqaamaabmaabaGaamyyaiabgkHiTiaaigdaaiaawIcacaGLPaaa<br />% daahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGIbWaaWbaaSqabeaaca<br />% aIYaaaaaaaaOqaamaalaaabaGaamOEaiabgUcaRiaaigdaaeaacaWG<br />% 6bGaeyOeI0IaaGymaaaacqGH9aqpdaWcaaqaaiaadggadaahaaWcbe<br />% qaaiaaikdaaaGccqGHRaWkcaWGIbWaaWbaaSqabeaacaaIYaaaaOGa<br />% eyOeI0IaaGymaaqaamaabmaabaGaamyyaiabgkHiTiaaigdaaiaawI<br />% cacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGIbWaaWba<br />% aSqabeaacaaIYaaaaaaakiabgkHiTmaacmaabaWaaSaaaeaacaaIYa<br />% GaamOyaaqaamaabmaabaGaamyyaiabgkHiTiaaigdaaiaawIcacaGL<br />% PaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGIbWaaWbaaSqabe<br />% aacaaIYaaaaaaaaOGaay5Eaiaaw2haaiaadMgaaeaaaeaacaqGbbGa<br />% ae4CaiaabMgacaqG6aGaaeiiaiGackfacaGGLbWaaiWaaeaadaWcaa<br />% qaaiaadQhacqGHRaWkcaaIXaaabaGaamOEaiabgkHiTiaaigdaaaaa<br />% caGL7bGaayzFaaGaeyypa0ZaaSaaaeaacaWGHbWaaWbaaSqabeaaca<br />% aIYaaaaOGaey4kaSIaamOyamaaCaaaleqabaGaaGOmaaaakiabgkHi<br />% TiaaigdaaeaadaqadaqaaiaadggacqGHsislcaaIXaaacaGLOaGaay<br />% zkaaWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOyamaaCaaaleqa<br />% baGaaGOmaaaaaaGccaqGSaGaaeiiaiaabMhacaqGGaGaaeiCaiaabg<br />% gacaqGYbGaaeyyaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaciOu<br />% aiaacwgadaGadaqaamaalaaabaGaamOEaiabgUcaRiaaigdaaeaaca<br />% WG6bGaeyOeI0IaaGymaaaaaiaawUhacaGL9baacqGH9aqpcaaIWaGa<br />% eyi1HS9aaSaaaeaacaWGHbWaaWbaaSqabeaacaaIYaaaaOGaey4kaS<br />% IaamOyamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaigdaaeaadaqa<br />% daqaaiaadggacqGHsislcaaIXaaacaGLOaGaayzkaaWaaWbaaSqabe<br />% aacaaIYaaaaOGaey4kaSIaamOyamaaCaaaleqabaGaaGOmaaaaaaGc<br />% cqGH9aqpcaaIWaaabaGaeyi1HSTaamyyamaaCaaaleqabaGaaGOmaa<br />% aakiabgUcaRiaadkgadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI<br />% XaGaeyypa0JaaGimaiabgsDiBlaadggadaahaaWcbeqaaiaaikdaaa<br />% GccqGHRaWkcaWGIbWaaWbaaSqabeaacaaIYaaaaOGaeyypa0JaaGym<br />% aaqaaaqaaiaabYeacaqG1bGaaeyzaiaabEgacaqGVbGaaeiiamaaem<br />% aabaGaamOEaaGaay5bSlaawIa7aiabg2da9iaaigdaaaaa!7671!<br />\[<br />\begin{gathered}<br /> {\text{Consideremos }}z = a + bi \in \mathbb{C} - \left\{ 1 \right\}{\text{, luego:}} \hfill \\<br /> \frac{{z + 1}}<br />{{z - 1}} = \frac{{a + bi + 1}}<br />{{a + bi - 1}} = \frac{{\left( {a + 1} \right) + bi}}<br />{{\left( {a - 1} \right) + bi}} = \frac{{\left\{ {\left( {a + 1} \right) + bi} \right\}\left\{ {\left( {a - 1} \right) - bi} \right\}}}<br />{{\left\{ {\left( {a - 1} \right) + bi} \right\}\left\{ {\left( {a - 1} \right) - bi} \right\}}} \hfill \\<br /> \frac{{z + 1}}<br />{{z - 1}} = \frac{{a^2 - 1 - bi\left( {a + 1} \right) + bi\left( {a - 1} \right) + b^2 }}<br />{{\left( {a - 1} \right)^2 + b^2 }} \hfill \\<br /> \frac{{z + 1}}<br />{{z - 1}} = \frac{{a^2 + b^2 - 1 + bi\left( {a - 1 - a - 1} \right)}}<br />{{\left( {a - 1} \right)^2 + b^2 }} \hfill \\<br /> \frac{{z + 1}}<br />{{z - 1}} = \frac{{a^2 + b^2 - 1 - 2bi}}<br />{{\left( {a - 1} \right)^2 + b^2 }} \hfill \\<br /> \frac{{z + 1}}<br />{{z - 1}} = \frac{{a^2 + b^2 - 1}}<br />{{\left( {a - 1} \right)^2 + b^2 }} - \left\{ {\frac{{2b}}<br />{{\left( {a - 1} \right)^2 + b^2 }}} \right\}i \hfill \\<br /> \hfill \\<br /> {\text{Asi: }}\operatorname{Re} \left\{ {\frac{{z + 1}}<br />{{z - 1}}} \right\} = \frac{{a^2 + b^2 - 1}}<br />{{\left( {a - 1} \right)^2 + b^2 }}{\text{, y para que }}\operatorname{Re} \left\{ {\frac{{z + 1}}<br />{{z - 1}}} \right\} = 0 \Leftrightarrow \frac{{a^2 + b^2 - 1}}<br />{{\left( {a - 1} \right)^2 + b^2 }} = 0 \hfill \\<br /> \Leftrightarrow a^2 + b^2 - 1 = 0 \Leftrightarrow a^2 + b^2 = 1 \hfill \\<br /> \hfill \\<br /> {\text{Luego }}\left| z \right| = 1 \hfill \\ <br />\end{gathered} <br />\]](/tex-image/3cbef85e79d74c95292c27796131246f.png) -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
 Mar 11 2012, 12:11 AM Mar 11 2012, 12:11 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.039 Registrado: 4-October 09 Desde: Valparaíso Miembro Nº: 59.794 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
A que se refiere eso de los "80 puntos"?
--------------------   |
|
|
|
 Mar 11 2012, 12:12 AM Mar 11 2012, 12:12 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.271 Registrado: 16-May 11 Miembro Nº: 88.746 |
A que se refiere eso de los "80 puntos"? Supongo que se le fue un 0 y debería ser 8 Puntos -------------------- cambié de cuenta, adiós |
|
|
|
 Mar 11 2012, 12:59 AM Mar 11 2012, 12:59 AM
Publicado:
#6
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 186 Registrado: 11-January 10 Miembro Nº: 65.010 Nacionalidad:  Sexo:  |
o quizas, debe ser que tiene que contestar un total de preguntas que sumen 80 puntos
|
|
|
|
 Mar 11 2012, 09:23 AM Mar 11 2012, 09:23 AM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
El problema 8 me tinca a buen propuesto para pedagogía.
Los demás son como "aplique la fórmula" -------------------- |
|
|
|
 Mar 11 2012, 01:05 PM Mar 11 2012, 01:05 PM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ditox, si te fijas cada pregunta tiene su puntaje. La gracia es que respondas un total de preguntas que sumen 80 puntos.
-------------------- Me voy, me jui.
|
|
|
|
 Feb 24 2013, 01:25 PM Feb 24 2013, 01:25 PM
Publicado:
#9
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 33 Registrado: 4-August 08 Miembro Nº: 31.437 Colegio/Liceo:  |
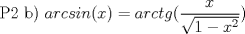 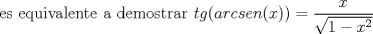 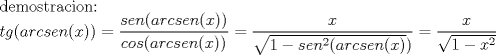
--------------------  Admisión 2013  Generación 2012 me gusta la química |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th February 2025 - 05:17 PM |












