n|a_n - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Teoría de Números > Problemas Propuestos

Reply to this topic

Start new topic

n|a_n

xD13G0x Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 6 2012, 12:53 PM Publicado: #1
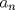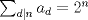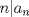Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad: Sexo:	Defina la secuencia $TEX: $a_n$$ por $TEX: $\sum_{d\|n}a_d=2^n$$ . Pruebe que $TEX: $n\|a_n$$ . -------------------- "I've never let my school interfere with my education.”

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 31 2017, 02:57 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Vamos a denotar $f(n)=a_n$, entonces debemos probar que $n\|f(n)$, donde $2^n=\sum_{d\|n}f(d)$. Lo primero es notar que $f(1)=2$. Sea $p$ un primo y $k>1$, entonces<br />\begin{center}$2^{p^k}=\sum_{d\|p^k}f(d)=\sum_{j=0}^k f(p^j)= f(p^k)+2^{p^{k-1}}$\end{center}<br />y por lo tanto $f(p^k)=2^{p^k}-2^{p^{k-1}}$ para $k>1$ y $f(p)=2^p-2$, pues $f(1)=2$.<br />Para $p\not=2$ tenemos que $2^p\equiv 2\mod p$ y así mediante el Lifting the exponent lemma<br />$$v_p(2^{p^2}-2^p)=v_p(2^p-2)+v_p(p)\ge 2.$$<br />Iterando este argumento se concluye que $p^k\|f(p^k)$. Por la fórmular de inversión de Moebius, y usando que $n\mapsto 2^n$ es multiplicativa, se deduce que $f$ es multiplicatica. Finalmente, usando que el resultado es cierto para potencias de primos, se concluye.$ Comentario: con inducción sale mucho más fácil pero no se puede visualizar la función. -------------------- blep

lang Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 31 2017, 03:02 PM Publicado: #3
Matemático Grupo: Validating Mensajes: 62 Registrado: 23-November 14 Miembro Nº: 134.118	CITA(snw @ Mar 31 2017, 02:57 PM) $TEX: Vamos a denotar $f(n)=a_n$, entonces debemos probar que $n\|f(n)$, donde $2^n=\sum_{d\|n}f(d)$. Lo primero es notar que $f(1)=2$. Sea $p$ un primo y $k>1$, entonces<br />\begin{center}$2^{p^k}=\sum_{d\|p^k}f(d)=\sum_{j=0}^k f(p^j)= f(p^k)+2^{p^{k-1}}$\end{center}<br />y por lo tanto $f(p^k)=2^{p^k}-2^{p^{k-1}}$ para $k>1$ y $f(p)=2^p-2$, pues $f(1)=2$.<br />Para $p\not=2$ tenemos que $2^p\equiv 2\mod p$ y así mediante el Lifting the exponent lemma<br />$$v_p(2^{p^2}-2^p)=v_p(2^p-2)+v_p(p)\ge 2.$$<br />Iterando este argumento se concluye que $p^k\|f(p^k)$. Por la fórmular de inversión de Moebius, y usando que $n\mapsto 2^n$ es multiplicativa, se deduce que $f$ es multiplicatica. Finalmente, usando que el resultado es cierto para potencias de primos, se concluye.$ Comentario: con inducción sale mucho más fácil pero no se puede visualizar la función. $TEX: $n \rightarrow 2^ n $$ multiplicativa?

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 31 2017, 03:06 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	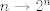CITA(lang @ Mar 31 2017, 04:02 PM) $TEX: $n \rightarrow 2^ n $$ multiplicativa? sheit, tienes razón. Bueno, quizás alguien termina el argumento -------------------- blep

lang Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 31 2017, 03:18 PM Publicado: #5
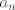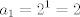Matemático Grupo: Validating Mensajes: 62 Registrado: 23-November 14 Miembro Nº: 134.118	Partiremos demostrando por induccion que $TEX: $a_n$$ es el numero de cadenas aperiodicas de 0s y 1s de largo n. En efecto $TEX: $$ a_1 = 2^1 = 2$$$ y hay dos cadenas de largo 1 aperiodicas (0 y 1). Si asumimos el resultado para k < n, entonces el numero de cadenas de largo n es 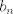$TEX: $2^n - b_n$$ donde $TEX: $b_n$$ es el numero de cadenas periodicas. 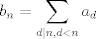Como el periodo divide a n, tenemos que $TEX: $$ b_n = \sum_{d \| n, d < n} a_ d$$$ de donde el numero de cadenas de largo n es 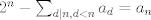$TEX: $2^n - \sum_{d \| n, d < n} a_ d = a_n$$ lo que termina la demostracion por induccion. Para terminar, sea A_n es conjunto de las cadenas aperiodicas de largo $TEX: $n$$ . 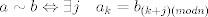Definimos la relacion de equivalencia $TEX: $$a \sim b \Leftrightarrow \exists j \quad a_k = b_{(k + j)(mod n)}$$$ La condicion de aperiodicidad nos dice que las clases de equivalencia tendran tamaño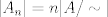 $TEX: $n$$ por lo que $TEX: $ \|A_n\| = n \|A / \sim \|$$ Mensaje modificado por lang el Mar 31 2017, 03:23 PM

« Posterior · Problemas Propuestos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 09:36 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.