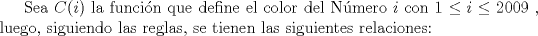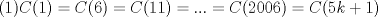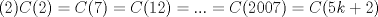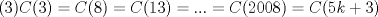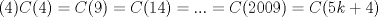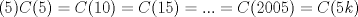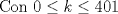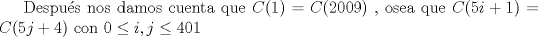|
|
|
|
|
|
|
  |
 Feb 1 2012, 01:38 PM Feb 1 2012, 01:38 PM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Colaborador Silver Mensajes: 423 Registrado: 4-January 11 Miembro Nº: 82.624 Nacionalidad:  Universidad: .png) Sexo:  |
IX CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT Fecha 4: 6 de Agosto del 2011 Tercer Nivel Individual Problema 1 Demuetre que si en un pentágono regular sus lados miden  y sus diagonales y sus diagonales  , entonces se tiene: , entonces se tiene: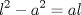 Problema 2 Existen 2011 colores disponibles. Cada elemento del conjunto: 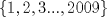 debe ser coloreado con uno de estos colores, de modo que: 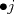 y y 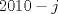 tienen el mismo color tienen el mismo color si si 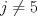 , entonces , entonces 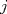 y y 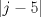 tienen el mismo color. tienen el mismo color.¿de cuantas maneras pueden ser coloreados los números? |
|
|
|
 Feb 1 2012, 02:36 PM Feb 1 2012, 02:36 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2
Saludos Mensaje modificado por Seba² el Feb 1 2012, 02:44 PM -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Feb 1 2012, 05:05 PM Feb 1 2012, 05:05 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 274 Registrado: 20-May 10 Miembro Nº: 71.064 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
  Saludos!! -------------------- 100% REAL NO FAKE 1 LINK MEGAUPLOAD KEYGEN + CRACK FULL HD 1080P SUBS ESPAÑOL [PORTABLE]
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 5th July 2025 - 01:25 PM |