Examen Cálculo diferencial e integral 2010/2

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Chile > Cálculo Diferencial

Examen Cálculo diferencial e integral 2010/2

Opciones

Shine Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2012, 11:42 PM Publicado: #1
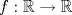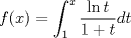Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.255 Registrado: 22-February 08 Miembro Nº: 15.777 Sexo:	Examen P1. 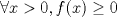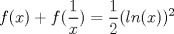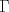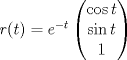Considere la función $TEX: $f: \mathbb{R}\to\mathbb{R}$$ definida por $TEX: $\displaystyle f(x)=\int_{1}^{x}\frac{\ln t}{1+t}dt$$ i) (1 punto)Demuestre que $TEX: $\forall x > 0, f(x)\geq 0$$ ii) (2 puntos) Demuestre que $TEX: $\displaystyle f(x)+ f(\frac{1}{x})= \frac{1}{2} (ln (x))^{2}$$ b.) (3 puntos) Considere la curva $TEX: $\Gamma$$ parametrizada por: $TEX: $r(t)= e^{-t}\begin{pmatrix}<br />\cos t\\ <br />\sin t<br />1<br />\end{pmatrix}$$ , donde $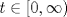TEX: $t\in [0,\infty)$$ Encuentre los vectores tangente T(t) y normal N(t) y el largo total de la curva 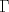$TEX: $\Gamma$$ P2. a.) (3 puntos) Un triángulo isóceles se inscribe en la elipse de ecuación 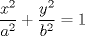$TEX: $\displaystyle \frac{x^{2}}{a^{2}}+ \frac{y^{2}}{b^{2}}=1$$ con el vértice en (a,0) y la base paralela al eje OY. Determine la altura del triángulo de área máxima y calcule dicha área. b.) (3 puntos) Calcular, para a>0 el valor de 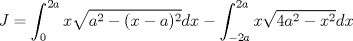$TEX: $\displaystyle J= \int_{0}^{2a}x\sqrt{a^{2}-(x-a)^{2}}dx- \int_{-2a}^{2a}x\sqrt{4a^{2}-x^{2}}dx$$ Indicación: Use, donde corresponda, propiedades de las integrales sobre funciones pares y/o impares P3 a.) Estudie la convergencia de las siguientes integrales, indicando su especie i) 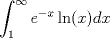$TEX: $\displaystyle \int_{1}^{\infty }e^{-x}\ln(x)dx$$ (1 punto) ii.) $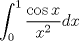TEX: $\displaystyle \int_{0}^{1}\frac{\cos x}{x^{2}}dx$$ (1 punto) b.) Estudie la convergencia absoluta y condicional de las series i) 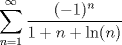$TEX: $\displaystyle \sum_{n=1}^{\infty }\frac{(-1)^{n}}{1+n+\ln(n)}$$ (1 punto) ii) $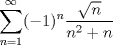TEX: $\displaystyle \sum_{n=1}^{\infty }(-1)^{n}\frac{\sqrt{n}}{n^{2}+n}$$ (1 punto) c) Recordando que 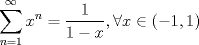$TEX: $\displaystyle \sum_{n=1}^{\infty }x^{n} = \frac{1}{1-x}, \forall x \in (-1,1)$$ , se pide: i) (1.5 puntos) Determinar las funciones f,g tales que sus series de potencias son: 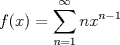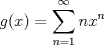$TEX: $\displaystyle f(x)= \sum_{n=1}^{\infty }nx^{n-1}$$ $TEX: $\displaystyle g(x)= \sum_{n=1}^{\infty }nx^{n} $$ ii) (0.5 puntos) Calcule el valor de la serie numérica: 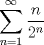$TEX: $\displaystyle \sum_{n=1}^{\infty }\frac{n}{2^{n}}$$ Tiempo: 3.0 horas Flojera... para el examen de mañana . Disfruten Mensaje modificado por Shine el Feb 12 2012, 07:53 PM