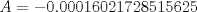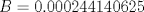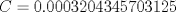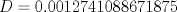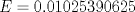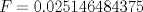|
|
|
|
|
|
|
  |
 Jan 10 2012, 02:48 PM Jan 10 2012, 02:48 PM
Publicado:
#1
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 95 Registrado: 24-September 07 Miembro Nº: 10.491 Nacionalidad:  Universidad:  Sexo:  |
Control 1 PEP 3 I.- II.- III.- Mensaje modificado por Ma.kiss el Jan 10 2012, 03:08 PM -------------------- |
|
|
|
 Jan 11 2012, 09:06 AM Jan 11 2012, 09:06 AM
Publicado:
#2
|
|
 Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 27-April 08 Desde: Rancagua Miembro Nº: 21.437 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Gracias, los haré hoy para la pep de mañana, éxito.
-------------------- Injusticias propagadas por la timidez Miedo al crecer ¡Esto no puede ser! Blasfemias al amanecer me atacan sin parar Trifulcas de sufrimiento agobian mi existencia.      |
|
|
|
 Jan 28 2012, 08:00 PM Jan 28 2012, 08:00 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.847 Registrado: 3-October 09 Miembro Nº: 59.760 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
se ve piola !
|
|
|
|
 Jan 29 2012, 09:03 AM Jan 29 2012, 09:03 AM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 18-May 11 Miembro Nº: 88.919 Nacionalidad:  Universidad:  Sexo:  |
1.a)
Espero que no haya algun error, este año quiero ser el super mechon flaite!! Mensaje modificado por Mauricio Muñoz el Jan 29 2012, 09:09 AM --------------------    |
|
|
|
 Jan 29 2012, 10:27 AM Jan 29 2012, 10:27 AM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 2-July 10 Desde: sdfs Miembro Nº: 73.602 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Espero que no haya algun error, este año quiero ser el super mechon flaite!! Okey -------------------- El de mi foto(avatar) es el fhurer, aunque no se si seguirá dando vueltas por aquí    Super chanta->
" El servir es una virtud de la mujer " Anita, dios sabe quien es. |
|
|
|
 Jan 30 2012, 10:51 PM Jan 30 2012, 10:51 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 539 Registrado: 21-January 11 Desde: Santiago - Osorno - Chile Miembro Nº: 83.254 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Aquí voy con el P.3
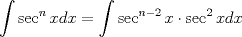 Usamos la fórmula de integración por partes: 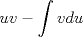 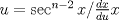 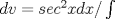 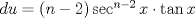 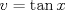 Retomando: 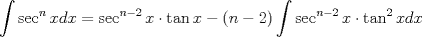 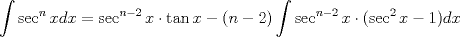 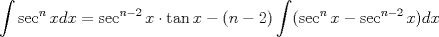 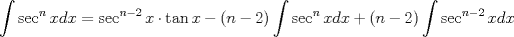 Si nos damos cuenta, tenemos la misma integral repetida en ambos lados, la despejamos únicamente y haciendo algunos arreglines algebraicos llegamos a que: 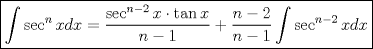 Que es la fórmula pedida, y se puede usar de manera repetitiva hasta que el grado baje al nivel deseado. Calculando 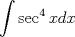 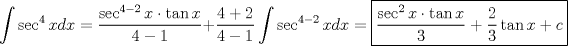
Mensaje modificado por E.Rodriguez el Jan 30 2012, 11:01 PM -------------------- Esteban A. Rodríguez M.
Ex- alumno Generación 2011 Colegio San Mateo-Osorno    "Por muy larga que sea la tormenta, el sol siempre vuelve a brillar entre las nubes" - Khalil Gibran |
|
|
|
 Jan 31 2012, 06:34 AM Jan 31 2012, 06:34 AM
Publicado:
#7
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 95 Registrado: 24-September 07 Miembro Nº: 10.491 Nacionalidad:  Universidad:  Sexo:  |
Si alguien se anima con la c) de la parte I, yo aún no logro resolverlo, no se me ocurre una forma de hacerlo "más corto". Y me sale tan monstruoso que lo abandono xD
-------------------- |
|
|
|
 Jan 31 2012, 08:39 AM Jan 31 2012, 08:39 AM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 18-May 11 Miembro Nº: 88.919 Nacionalidad:  Universidad:  Sexo:  |
Si alguien se anima con la c) de la parte I, yo aún no logro resolverlo, no se me ocurre una forma de hacerlo "más corto". Y me sale tan monstruoso que lo abandono xD Estaba aburrido y empece a meterle mano. Fue muy tentador separar la expresion en fracciones parciales, pero se llega a algo muy muy feo: 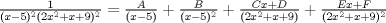 Aqui los resultados: Te recomiendo hecharle una revizada a mis resultados, los números son feos así que es muy posible que me haya equivocado en algun númerito o signo antes de resolver el sistema. --------------------    |
|
|
|
 Jan 31 2012, 09:46 AM Jan 31 2012, 09:46 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 539 Registrado: 21-January 11 Desde: Santiago - Osorno - Chile Miembro Nº: 83.254 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Estaba aburrido y empece a meterle mano. Fue muy tentador separar la expresion en fracciones parciales, pero se llega a algo muy muy feo: 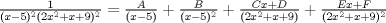 Aqui los resultados: Te recomiendo hecharle una revizada a mis resultados, los números son feos así que es muy posible que me haya equivocado en algun númerito o signo antes de resolver el sistema. Sí, esos son los coeficientes, mensa pajita que te mandaste haciendo esa weá XDD, me da la impresión que no es la idea del ejercicio, queda algo demasiado largo, y despues queda una integral no muy linda de evaluar :S -------------------- Esteban A. Rodríguez M.
Ex- alumno Generación 2011 Colegio San Mateo-Osorno    "Por muy larga que sea la tormenta, el sol siempre vuelve a brillar entre las nubes" - Khalil Gibran |
|
|
|
 Jan 6 2016, 09:36 AM Jan 6 2016, 09:36 AM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 579 Registrado: 17-April 11 Miembro Nº: 87.233 Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 12th April 2025 - 07:25 AM |





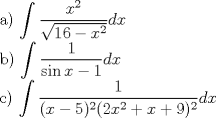
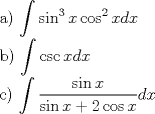
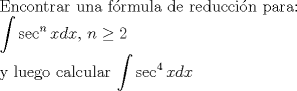






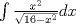
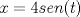
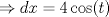
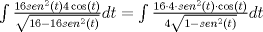
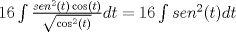
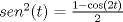
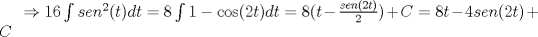
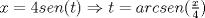
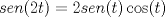
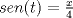
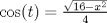

 <!--SPOILER DIV-->
<!--SPOILER DIV-->