|
|
|
|
|
|
|
  |
 Mar 29 2007, 05:05 PM Mar 29 2007, 05:05 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
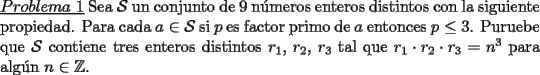 Solucion: (Pendiente)  Solucion:  Solucion: (Pendiente) 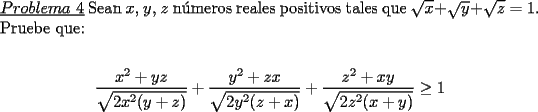 Solucion:  Solucion: |
|
|
|
 Mar 29 2007, 05:26 PM Mar 29 2007, 05:26 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Solución P4:
 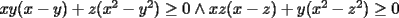 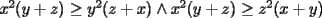 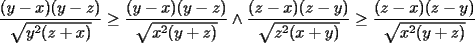 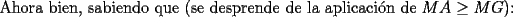 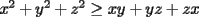 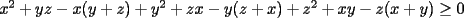 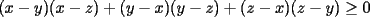 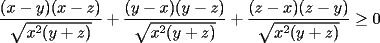 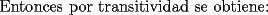 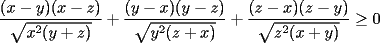 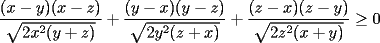 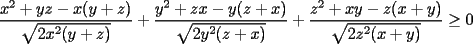 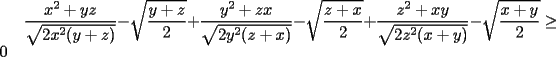 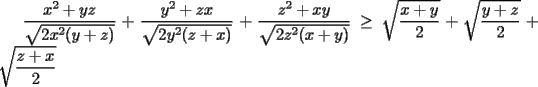 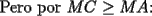 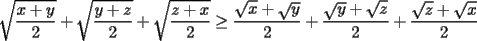 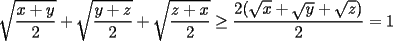  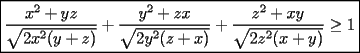 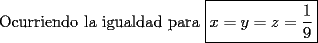 |
|
|
|
 Jun 4 2007, 11:13 PM Jun 4 2007, 11:13 PM
Publicado:
#3
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 19-July 06 Desde: Conce, Jazz Capitol Miembro Nº: 1.716 Nacionalidad:  Sexo:  |
|
|
|
|
 Jun 15 2007, 02:10 PM Jun 15 2007, 02:10 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Resultó simple la solución al siguiente problema. Si quieren más detalles, pueden preguntar.
Solución al problema 3 Dados dos números: i, j en el conjunto {1,2,...,n}, diremos que el par (i,j) es bueno si el círculo Ci contiene propiamente al círculo Cj. Algunas propiedades evidentes (considerando i, j como en esta definición):
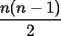 . Esta cota superior puede ser alcanzada, como muestra el siguiente arreglo (daré una descripción cartesiana de los círculos): . Esta cota superior puede ser alcanzada, como muestra el siguiente arreglo (daré una descripción cartesiana de los círculos):
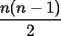 . .
-------------------- |
|
|
|
 Jul 25 2007, 12:26 AM Jul 25 2007, 12:26 AM
Publicado:
#5
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 19-July 06 Desde: Conce, Jazz Capitol Miembro Nº: 1.716 Nacionalidad:  Sexo:  |
Para cada i en el conjunto {1,2,...,n-1}, la circunferencia de Ci pasa por el punto de coordenadas (2i,0), que es el centro del círculo Ci+1. Pero de acuerdo al enunciado se supone que es la circunferencia 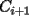 la que debe pasar por el centro de la que debe pasar por el centro de 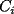 . . Mensaje modificado por Vicho_Correa el Jul 25 2007, 12:28 AM |
|
|
|
 Aug 5 2007, 01:06 AM Aug 5 2007, 01:06 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Ups es cierto, xsebastian tiene que arreglar ese problema, por mientras el problema sigue en pie.
Gracias |
|
|
|
 Aug 19 2007, 05:30 PM Aug 19 2007, 05:30 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
Ojalá que esté bien, además mi redacción no es de las mejores.
![TEX: \[<br />\begin{gathered}<br /> \boxed{S_1 } \hfill \\<br /> r_1 = 2^{q_1 } 3^{p_1 } \hfill \\<br /> r_2 = 2^{q_2 } 3^{p_2 } \hfill \\<br /> r_3 = 2^{q_3 } 3^{p_3 } \hfill \\<br /> \vdots \hfill \\<br /> r_9 = 2^{q_9 } 3^{p_9 } \hfill \\<br /> {\text{Se cumple lo pedido}} \Leftrightarrow \left. 3 \right|q_x + q_y + q_z \wedge \left. 3 \right|p_x + p_y + p_z \hfill \\<br /> \hfill \\<br /> {\text{Como todo numero divido por 3}}{\text{, deja resto 0}} \vee {\text{1}} \vee 2,{\text{ los elementos de }}S \hfill \\<br /> {\text{podemos clasificarlos en estos 9 subconjuntos}} \hfill \\<br /> 2^{q_a } 3^{p_a } \in S_{0a} \Leftrightarrow \forall q_a ,p_a {\text{ se cumple que: }}q_a \equiv 0\bmod 3 \wedge p_a \equiv 0\bmod 3 \hfill \\<br /> 2^{q_b } 3^{p_b } \in S_{0b} \Leftrightarrow \forall q_b ,p_b {\text{ se cumple que: }}q_b \equiv 0\bmod 3 \wedge p_b \equiv 1\bmod 3 \hfill \\<br /> 2^{q_c } 3^{p_c } \in S_{0c} \Leftrightarrow \forall q_c ,p_c {\text{ se cumple que: }}q_c \equiv 0\bmod 3 \wedge p_c \equiv 2\bmod 3 \hfill \\<br /> 2^{q_d } 3^{p_d } \in S_{1a} \Leftrightarrow \forall q_d ,p_d {\text{ se cumple que: }}q_d \equiv 1\bmod 3 \wedge p_d \equiv 0\bmod 3 \hfill \\<br /> 2^{q_e } 3^{p_e } \in S_{1b} \Leftrightarrow \forall q_e ,p_e {\text{ se cumple que: }}q_e \equiv 1\bmod 3 \wedge p_e \equiv 1\bmod 3 \hfill \\<br /> 2^{q_f } 3^{p_f } \in S_{1c} \Leftrightarrow \forall q_f ,p_f {\text{ se cumple que: }}q_f \equiv 1\bmod 3 \wedge p_f \equiv 2\bmod 3 \hfill \\<br /> 2^{q_g } 3^{p_g } \in S_{2a} \Leftrightarrow \forall q_g ,p_g {\text{ se cumple que: }}q_g \equiv 2\bmod 3 \wedge p_g \equiv 0\bmod 3 \hfill \\<br /> 2^{q_h } 3^{p_h } \in S_{2b} \Leftrightarrow \forall q_h ,p_h {\text{ se cumple que: }}q_h \equiv 2\bmod 3 \wedge p_h \equiv 1\bmod 3 \hfill \\<br /> 2^{q_i } 3^{p_i } \in S_{2c} \Leftrightarrow \forall q_i ,p_i {\text{ se cumple que: }}q_i \equiv 2\bmod 3 \wedge p_i \equiv 2\bmod 3 \hfill \\ <br />\end{gathered} <br />\]](./tex/1187752430.gif) ![TEX: \[<br />\begin{gathered}<br /> {\text{Caso 1}} \hfill \\<br /> {\text{Si al menos 3 de los elementos pertenecen al mismo subconjunto }}S_i {\text{ se cumple}} \hfill \\<br /> {\text{lo pedido}}{\text{.}} \hfill \\<br /> {\text{Dem 1:}} \hfill \\<br /> {\text{Al sumar tres numeros con el mismo resto al ser divido por 3}}{\text{, se obtiene que}} \hfill \\<br /> {\text{la suma es divisible por 3}} \hfill \\<br /> a \equiv 0\bmod 3,b \equiv 0\bmod 3,c \equiv 0\bmod 3 \Rightarrow a + b + c \equiv 0\bmod 3 \hfill \\<br /> a \equiv 1\bmod 3,b \equiv 1\bmod 3,c \equiv 1\bmod 3 \Rightarrow a + b + c \equiv 3 \equiv 0\bmod 3 \hfill \\<br /> a \equiv 2\bmod 3,b \equiv 2\bmod 3,c \equiv 2\bmod 3 \Rightarrow a + b + c \equiv 6 \equiv 0\bmod 3 \hfill \\ <br />\end{gathered} <br />\]](./tex/1187752588.gif) ![TEX: \[<br />\begin{gathered}<br /> {\text{Caso 2}} \hfill \\<br /> {\text{Supongamos que a lo mas hay elementos por cada subconjunto }}\left( {{\text{para que no}}} \right. \hfill \\<br /> \left. {{\text{se cumpla el Caso 1}}} \right). \hfill \\<br /> {\text{Cada subconjunto posee a lo mas dos elementos}}{\text{, y como son 9 elementos}} \hfill \\<br /> {\text{habran por lo menos 5 subconjuntos con elementos}}{\text{. Notemos que podemos}} \hfill \\<br /> {\text{clasificar a estos subconjuntos en las siguientes categorias:}} \hfill \\<br /> \boxed{S_{0a} ,S_{0b} ,S_{0c} } \hfill \\<br /> \boxed{S_{1a} ,S_{1b} ,S_{1c} } \hfill \\<br /> \boxed{S_{2a} ,S_{2b} ,S_{2c} } \hfill \\<br /> \hfill \\<br /> \boxed{S_{0a} ,S_{1a} ,S_{2a} } \hfill \\<br /> \boxed{S_{0b} ,S_{1b} ,S_{2b} } \hfill \\<br /> \boxed{S_{0c} ,S_{1c} ,S_{2c} } \hfill \\<br /> \hfill \\<br /> \boxed{S_{0a} ,S_{1b} ,S_{2c} } \hfill \\<br /> \boxed{S_{0a} ,S_{1c} ,S_{2b} } \hfill \\<br /> \boxed{S_{0b} ,S_{1a} ,S_{2c} } \hfill \\<br /> \boxed{S_{0b} ,S_{1c} ,S_{2a} } \hfill \\<br /> \boxed{S_{0c} ,S_{1a} ,S_{2b} } \hfill \\<br /> \boxed{S_{0c} ,S_{1b} ,S_{2a} } \hfill \\<br /> \hfill \\<br /> {\text{Es evidente que siempre habra una categoria donde todos sus subconjuntos}} \hfill \\<br /> {\text{tengan por lo menos un elemento}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{Finalmente tendremos que demostrar; si cada subconjunto de una categoria}} \hfill \\<br /> {\text{posee al menos un elemento se cumple lo pedido}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](./tex/1187752359.gif) ![TEX: \[<br />\begin{gathered}<br /> Lema \hfill \\<br /> {\text{Las categorias de la forma }}\boxed{S_{ta} ,S_{tb} ,S_{tc} }{\text{ cumple lo pedido}} \hfill \\<br /> {\text{Dem 2:}} \hfill \\<br /> {\text{Notemos que todos los conjuntos de la forma }}S_{ta} ,S_{tb} ,S_{tc} {\text{ posee cada uno}} \hfill \\<br /> {\text{un }}q{\text{ con el mismo resto}}{\text{, entonces por la Dem }}1{\text{ se cumple lo pedido}} \hfill \\<br /> {\text{para }}q. \hfill \\<br /> {\text{Notemos tambien que }} \hfill \\<br /> S_{ta} {\text{ posee un }}p_{ta} \equiv 0\bmod 3 \hfill \\<br /> S_{tb} {\text{ posee un }}p_{tb} \equiv 1\bmod 3 \hfill \\<br /> S_{tc} {\text{ posee un }}p_{tc} \equiv 2\bmod 3 \hfill \\<br /> \Rightarrow {\text{ }}p_{ta} + p_{tb} + p_{tc} \equiv 3 \equiv 0\bmod 3 \hfill \\<br /> {\text{Demostrando asi nuestro }}Lema \hfill \\<br /> \hfill \\<br /> Lema{\text{ 2}} \hfill \\<br /> {\text{Las categorias de la forma }}\boxed{S_{0p} ,S_{1p} ,S_{2p} }{\text{ cumple lo pedido}} \hfill \\<br /> Dem{\text{ 3:}} \hfill \\<br /> {\text{Basta leer la dem 2 y cambiar las }}q{\text{ por las }}p. \hfill \\<br />\end{gathered} <br />\]](./tex/1187752370.gif) ![TEX: \[<br />\begin{gathered}<br /> {\text{Lema 3}} \hfill \\<br /> {\text{Las categorias de la forma }}S_{0m} ,S_{1n} ,S_{2r} {\text{ cumplen lo pedido}}{\text{.}} \hfill \\<br /> {\text{Dem 4}} \hfill \\<br /> {\text{Como definimos anteriormente es claro que }}S_{0m} {\text{ posee un 2}}^{q_m } 3^{p_m } {\text{ tal que}} \hfill \\<br /> q_m \equiv 0\bmod 3.{\text{ Analogamente }}S_{1n} {\text{ y }}S_{2r} {\text{ poseen }}q's{\text{ tal que son }}q_n \equiv 1\bmod 3 \hfill \\<br /> {\text{y }}q_r \equiv 2\bmod 3. \hfill \\<br /> {\text{Luego notemos que }}S_{0m} ,S_{1n} ,S_{2r} {\text{ poseen cada uno un 2}}^q 3^p {\text{ tal que sus}} \hfill \\<br /> p{\text{ tienen residuos distintos entre si al ser dividos por tres}}{\text{.}} \hfill \\<br /> {\text{Tomando la demo 2 el razonamiento es analogo para }}q{\text{ y }}p \hfill \\<br /> \hfill \\<br /> {\text{Con esto finaliza la demostracion pues siempre se cumple el Caso 1 o el Caso 2}} \hfill \\<br /> {\text{P}}{\text{.S: Notar que el }}Lema{\text{ }}3{\text{ es mas general que el }}Lema{\text{ }}2. \hfill \\ <br />\end{gathered} <br />\]](./tex/1187752826.gif) Editado. Mensaje modificado por caf_tito el Aug 21 2007, 10:21 PM -------------------- |
|
|
|
 Aug 19 2007, 07:23 PM Aug 19 2007, 07:23 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
|
|
|
|
 Aug 19 2007, 07:54 PM Aug 19 2007, 07:54 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
Por qué es evidente??? Contraejemplo: 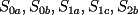 Creo que tu idea de agrupar es muy buena, pero creo que te faltó poner talvez unas 6 categorias más que debes analizar para dar por correcta tu solución Saludos -------------------- |
|
|
|
 Aug 25 2007, 07:24 PM Aug 25 2007, 07:24 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Ahora que agregaste estas 6 nuevas categorias, es cierto que siempre hay una con los 3 subconjuntos con almenos 1 elemento; pero no es tan evidente como tu lo plateas, me gustaria que argumentaras bien eso para darla por correcta de modo que quede a la comprensión de todos.
Saludos |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:22 PM |






![TEX: <br />\[<br />\begin{gathered}<br /> {\text{Tengamos en cuenta que H debe estar al interior del }}\vartriangle ABC.{\text{ Sea D el pie de la altura bajada }} \hfill \\<br /> {\text{desde C}}{\text{. Notemos que I no puede estar al interior del }}\vartriangle ADC.{\text{ En efecto}}{\text{, de no ser as\'i }}{\text{, se }} \hfill \\<br /> {\text{tendr\'ia que }}\angle ACI < 30 \Rightarrow \angle ACB < 60.{\text{ Adem\'as}}{\text{, I no puede estar a interior del }}\vartriangle BHC.{\text{ En }} \hfill \\<br /> {\text{efecto}}{\text{, de no ser as\'i }}{\text{, se tendr\'ia que }}\angle ABI > 30 \Rightarrow \angle ABC > 60.{\text{ Luego}}{\text{, I debe estar al interior }} \hfill \\<br /> {\text{del }}\vartriangle DBH.{\text{ Sea }}\angle {\text{ACB = }}\beta {\text{. Notemos que }}\angle {\text{BHC = 120 y que }}\angle {\text{BIC = 180 - }}\left( {\frac{\beta }<br />{{\text{2}}} + 60 - \frac{\beta }<br />{{\text{2}}}} \right) = .{\text{ }} \hfill \\<br /> {\text{120. Luego}}{\text{, el cuadril\'atero BIHC es c\'iclico}}{\text{, de donde }}\angle {\text{IHB = }}\frac{\beta }<br />{{\text{2}}}.{\text{ Adem\'as}}{\text{, }}\angle AHB = 180 - \beta {\text{, de }} \hfill \\<br /> {\text{donde }}\angle AHI = 180 - \frac{{3\beta }}<br />{2}{\text{. Ahora es f\'acil concluir lo pedido}}{\text{, teniendo en cuenta que }} \hfill \\<br /> \angle ABC = 120 - \beta . \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/1181016789.gif)




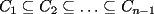 son evidentes, porque el punto de coordenadas (0,0) es el punto de tangencia de todas sus circunferencias, porque el eje Y es tangente común a todos ellos, y porque sus centros están ubicados sobre la parte positiva del eje X, en el orden adecuado (prefiero que hagan un dibujo y lo entiendan intuitivamente, antes de llenar de fórmulas).
son evidentes, porque el punto de coordenadas (0,0) es el punto de tangencia de todas sus circunferencias, porque el eje Y es tangente común a todos ellos, y porque sus centros están ubicados sobre la parte positiva del eje X, en el orden adecuado (prefiero que hagan un dibujo y lo entiendan intuitivamente, antes de llenar de fórmulas).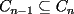 , lo cual también dejo de verificación al lector
, lo cual también dejo de verificación al lector

![TEX: \[<br />\begin{gathered}<br /> {\text{Caso 2}} \hfill \\<br /> {\text{Supongamos que a lo mas hay 2 elementos por cada subconjunto (para que no}} \hfill \\<br /> {\text{se cumpla el Caso 1)}}{\text{.}} \hfill \\<br /> {\text{Cada subconjunto posee a lo mas dos elementos}}{\text{,y como son 9 elementos}} \hfill \\<br /> {\text{habran por lo menos 5 subconjuntos con elementos}}{\text{.Notemos que podemos}} \hfill \\<br /> {\text{clasificar a estos subconjuntos en las siguientes categorias:}} \hfill \\<br /> \boxed{S_{0a} ,S_{0b} ,S_{0c} } \hfill \\<br /> \boxed{S_{1a} ,S_{1b} ,S_{1c} } \hfill \\<br /> \boxed{S_{2a} ,S_{2b} ,S_{2c} } \hfill \\<br /> \boxed{S_{0a} ,S_{1a} ,S_{2a} } \hfill \\<br /> \boxed{S_{0b} ,S_{1b} ,S_{2b} } \hfill \\<br /> \boxed{S_{0c} ,S_{1c} ,S_{2c} } \hfill \\<br /> {\text{Es evidente que siempre habra una categoria donde todos sus}} \hfill \\<br /> {\text{subconjuntos tengan por lo menos un elemento}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{Finalemente tendremos que demostrar que si cada subconjunto de una categoria}} \hfill \\<br /> {\text{posee al menos un elemento se cumple lo pedido}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](./tex/1187562650.gif)