|
|
|
|
|
|
|
  |
 Dec 8 2011, 04:19 PM Dec 8 2011, 04:19 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
El objetivo de esta maratón es que entre todos los usuarios que quieran participar lo hagan (sin verse afectados de sus experticia en el tema) y así lo pasemos bien, además de que también todos aquellos usuarios con ganas de introducirse en el mundo de la Geometría en Olimpiadas puedan hacerlo, por lo tanto, los ejercicios a postear deben tener un grado de dificultad que varíe entre no tan fácil y difícil, así motivamos a los distintos usuarios a participar de esta maratón.
Las reglas son las siguientes:
En un triángulo 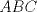 cualquiera cualquiera 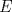 y y 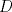 son puntos interiores de son puntos interiores de 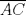 y y 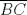 respectivamente. Luego, se tiene un punto respectivamente. Luego, se tiene un punto 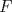 de forma que de forma que 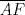 bisecta a bisecta a 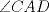 , y , y 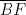 bisecta bisecta 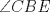 . Demuestre que . Demuestre que 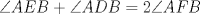 Recuerden que para este y los futuros problemas, las soluciones deben ser en lo posible, claras. Saludos. Mensaje modificado por El Geek el Dec 8 2011, 04:40 PM -------------------- Me voy, me jui.
|
|
|
|
 Dec 8 2011, 05:07 PM Dec 8 2011, 05:07 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Acá va mi solución:
Saludos Mensaje modificado por Seba² el Dec 8 2011, 05:40 PM -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Dec 8 2011, 05:44 PM Dec 8 2011, 05:44 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solución correcta, proponga. La fuente es conocidísima: challenging problems in geometry.
Saludos. PD: publicidad -------------------- Me voy, me jui.
|
|
|
|
 Dec 8 2011, 05:55 PM Dec 8 2011, 05:55 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Se tiene un punto
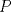 en el interior de un rectangulo en el interior de un rectangulo 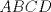 de tal manera que de tal manera que 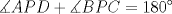 . Encuentre la suma de los angulos . Encuentre la suma de los angulos 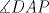 y y 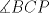 . .
-------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Dec 8 2011, 07:48 PM Dec 8 2011, 07:48 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 Sea 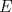 tal que [ tal que [ ![TEX: \[\overrightarrow {PE} \]](/tex-image/895a2b667b5ab7e35d10c0c6a3fe5020.png) paralelo a paralelo a 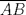 y el triángulo DPA es congruente al triángulo CEB, por esto, como y el triángulo DPA es congruente al triángulo CEB, por esto, como 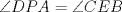 y y  , entonces el cuadrilátero PDEC es cíclico, luego , entonces el cuadrilátero PDEC es cíclico, luego 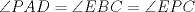 . Luego, por el paralelismo de PE respecto de las bases, entonces PE es perpendicular a BC, luego . Luego, por el paralelismo de PE respecto de las bases, entonces PE es perpendicular a BC, luego 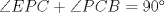 , pero , pero 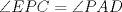 , entonces , entonces 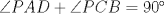 . .Saludos. Mensaje modificado por El Geek el Dec 8 2011, 08:07 PM -------------------- Me voy, me jui.
|
|
|
|
 Dec 8 2011, 08:12 PM Dec 8 2011, 08:12 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solución Correcta, ahora proponga uno Geek
La Fuente: Isacus Newtonus me pasó este problema, no me sé bien la fuente xD. Saludos -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 Dec 8 2011, 09:03 PM Dec 8 2011, 09:03 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Se me ha pedido que proponga yo, puesto que este es un problema bonito, simpatico, no dificil pero que el geek no ha resuelto y en vista de que no se quiere postear alguna burrada dificil aun, aqui vamos:
 Arreglada la pifia de planteo xD Mensaje modificado por Kaissa el Dec 8 2011, 09:10 PM -------------------- |
|
|
|
 Dec 8 2011, 10:12 PM Dec 8 2011, 10:12 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 274 Registrado: 20-May 10 Miembro Nº: 71.064 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Saludos! -------------------- 100% REAL NO FAKE 1 LINK MEGAUPLOAD KEYGEN + CRACK FULL HD 1080P SUBS ESPAÑOL [PORTABLE]
|
|
|
|
 Dec 9 2011, 08:00 AM Dec 9 2011, 08:00 AM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
Permitanme mi aporte.
Saludos. Mejor explicacion de algunas cosas: XT=TY pues en el triangulo ASB, SM es mediana y XY//AB PX=XY pues en el triangulo ADB, DM es mediana y PY//AB Mensaje modificado por cev el Dec 10 2011, 07:30 AM
Archivo(s) Adjunto(s)
-------------------- |
|
|
|
 Dec 9 2011, 09:16 PM Dec 9 2011, 09:16 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Bueno, dado que ya casi han pasado 24 hrs y Kaissa aún no ha aparecido para validar la solución de Sushi_8, la valido yo para que el show continúe.
Proponga señor Enzo. -------------------- Me voy, me jui.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:55 PM |
















