|
|
|
|
|
|
|
  |
 Dec 2 2011, 12:05 PM Dec 2 2011, 12:05 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 1-April 10 Miembro Nº: 67.566 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Hola, tengo el siguiente ejercicio:
Demostrar que 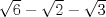 es irracional. es irracional.Lo intenté resolver usando la siguiente fórmula: 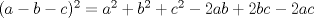 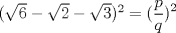 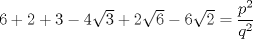 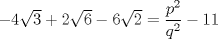 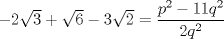 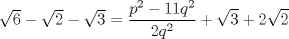 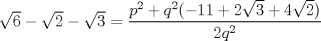 Quería saber si hice el procedimiento correctamente. Desde ya muchas gracias. Mensaje modificado por fede0563 el Dec 2 2011, 12:11 PM |
|
|
|
 Dec 2 2011, 12:07 PM Dec 2 2011, 12:07 PM
Publicado:
#2
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 372 Registrado: 20-December 10 Desde: Colina Miembro Nº: 82.064 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No se ve nada XD
-------------------- Medicion de mi esfuerzo:
66 paginas densas de calculos 20 ensayos "robados" a los preus XD ~2300 ejercicios en puntajenacional.cl ~500 ejercicios en mi preu Y subiendo cada dia! Si no saco más de 800, me corto uno, y lo dono XDD Informatica USM alla voy! xD |
|
|
|
 Dec 2 2011, 12:12 PM Dec 2 2011, 12:12 PM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 1-April 10 Miembro Nº: 67.566 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ya arreglé el inconveniente
|
|
|
|
 Dec 2 2011, 09:42 PM Dec 2 2011, 09:42 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 11-April 10 Desde: Santiago Miembro Nº: 68.358 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No es demasiado simple??
Raiz de 2 y raiz de 3 son irracionales. Su suma es irracional. La suma de cualquier irracional con un racional es siempre irracional. Por lo tanto, esa expresion es irracional Fin |
|
|
|
 Dec 2 2011, 10:39 PM Dec 2 2011, 10:39 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No es demasiado simple?? Raiz de 2 y raiz de 3 son irracionales. Su suma es irracional. La suma de cualquier irracional con un racional es siempre irracional. Por lo tanto, esa expresion es irracional Fin La suma de dos irracionales no es siempre irracional. La prueba no ha llegado a su Fin. |
|
|
|
 Dec 2 2011, 11:04 PM Dec 2 2011, 11:04 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 11-April 10 Desde: Santiago Miembro Nº: 68.358 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No siempre es irracional??
Contraejemplo? |
|
|
|
 Dec 2 2011, 11:10 PM Dec 2 2011, 11:10 PM
Publicado:
#7
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 274 Registrado: 20-May 10 Miembro Nº: 71.064 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
-------------------- 100% REAL NO FAKE 1 LINK MEGAUPLOAD KEYGEN + CRACK FULL HD 1080P SUBS ESPAÑOL [PORTABLE]
|
|
|
|
 Dec 2 2011, 11:11 PM Dec 2 2011, 11:11 PM
Publicado:
#8
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 18-August 11 Miembro Nº: 93.098 |
jaja me ganaron, xddd
pero hay otro ejemplo que es sumando dos en ambos lados, osea lo mismo xddd esto de las matematicas Mensaje modificado por h1s0k4 el Dec 2 2011, 11:12 PM |
|
|
|
 Dec 2 2011, 11:11 PM Dec 2 2011, 11:11 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 11-April 10 Desde: Santiago Miembro Nº: 68.358 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Descartando obviamente el caso trivial cuando un irracional es el inverso aditivo del otro. Intuitivamente diría que sí lo son. Aunque la intuición falla algunas veces.
Pero habría que ver alguna prueba formal. |
|
|
|
 Dec 2 2011, 11:21 PM Dec 2 2011, 11:21 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 11-April 10 Desde: Santiago Miembro Nº: 68.358 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
La pregunta de abstracción sería:
"Puedo expresar un racional como una combinación algebraica de irracionales (de módulos distintos)??" Pero no se ve muy fácil de demostrar aquello xD |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:03 PM |











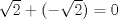 y el cero es racional
y el cero es racional