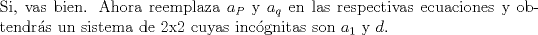P.A - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Álgebra > Progresiones: Aritmética y Geométrica

2 Páginas:

1 2 >

Reply to this topic

Start new topic

P.A

kkcoro3 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 23 2011, 05:59 PM Publicado: #1
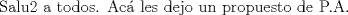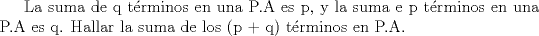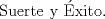Dios Matemático Grupo: Usuario FMAT Mensajes: 354 Registrado: 2-April 11 Desde: Temuco Miembro Nº: 86.120 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Salu2 a todos. Acá les dejo un propuesto de P.A.$ $TEX: La suma de q términos en una P.A es p, y la suma e p términos en una P.A es q. <br /> Hallar la suma de los (p + q) términos en P.A.$ $TEX: Suerte y Éxito.$ -------------------- $TEX: Suerte y Éxito. Nos vemos.$

alexis parra Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 24 2011, 12:05 AM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad: Sexo:	Sea $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaaaaa!37C0!<br />\[{a_1}\]$ el primer termino de la P.A y sea d la diferencia de la P.A La suma de los primeros q terminos es $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaakiaacIcacaWGXbGaeyOeI0IaaGOmaiaacMca<br />% cqGHRaWkcaWGKbGaaiikaiaadghacqGHsislcaaIXaGaaiykaiabg2<br />% da9iaadchaaaa!437F!<br />\[{a_1}(q - 2) + d(q - 1) = p\]$ La suma de los primeros p terminos es $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaakiaacIcacaWGWbGaeyOeI0IaaGOmaiaacMca<br />% cqGHRaWkcaWGKbGaaiikaiaadchacqGHsislcaaIXaGaaiykaiabg2<br />% da9iaadghaaaa!437E!<br />\[{a_1}(p - 2) + d(p - 1) = q\]$ Por lo tanto $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgU<br />% caRiaadghacqGH9aqpcaWGHbWaaSbaaSqaaiaaigdaaeqaaOWaamWa<br />% aeaacaWGWbGaey4kaSIaamyCaiabgkHiTiaaisdaaiaawUfacaGLDb<br />% aacqGHRaWkcaWGKbWaamWaaeaacaWGWbGaey4kaSIaamyCaiabgkHi<br />% TiaaikdacaGGPaaacaGLBbGaayzxaaaaaa!4AE7!<br />\[p + q = {a_1}\left[ {p + q - 4} \right] + d\left[ {p + q - 2)} \right]\]$ Espero respuesta.

tochalo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 24 2011, 12:28 AM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 426 Registrado: 13-January 08 Desde: desde la pieza de tu hermana Miembro Nº: 14.612 Nacionalidad: Colegio/Liceo: Sexo:	CITA(alexis parra @ Jul 24 2011, 02:05 AM) Sea $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaaaaa!37C0!<br />\[{a_1}\]$ el primer termino de la P.A y sea d la diferencia de la P.A La suma de los primeros q terminos es $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaakiaacIcacaWGXbGaeyOeI0IaaGOmaiaacMca<br />% cqGHRaWkcaWGKbGaaiikaiaadghacqGHsislcaaIXaGaaiykaiabg2<br />% da9iaadchaaaa!437F!<br />\[{a_1}(q - 2) + d(q - 1) = p\]$ La suma de los primeros p terminos es $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaakiaacIcacaWGWbGaeyOeI0IaaGOmaiaacMca<br />% cqGHRaWkcaWGKbGaaiikaiaadchacqGHsislcaaIXaGaaiykaiabg2<br />% da9iaadghaaaa!437E!<br />\[{a_1}(p - 2) + d(p - 1) = q\]$ Por lo tanto $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgU<br />% caRiaadghacqGH9aqpcaWGHbWaaSbaaSqaaiaaigdaaeqaaOWaamWa<br />% aeaacaWGWbGaey4kaSIaamyCaiabgkHiTiaaisdaaiaawUfacaGLDb<br />% aacqGHRaWkcaWGKbWaamWaaeaacaWGWbGaey4kaSIaamyCaiabgkHi<br />% TiaaikdacaGGPaaacaGLBbGaayzxaaaaaa!4AE7!<br />\[p + q = {a_1}\left[ {p + q - 4} \right] + d\left[ {p + q - 2)} \right]\]$ Espero respuesta. $TEX: \noindent<br />La idea es que a partir de los datos puedas encontrar $a_1$ y $d$, pues de esta forma la P.A queda determinada$

alexis parra Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 24 2011, 12:29 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad: Sexo:	CITA(tochalo @ Jul 24 2011, 01:28 AM) $TEX: \noindent<br />La idea es que a partir de los datos puedas encontrar $a_1$ y $d$, pues de esta forma la P.A queda determinada$

kkcoro3 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 24 2011, 01:26 AM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 354 Registrado: 2-April 11 Desde: Temuco Miembro Nº: 86.120 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(alexis parra @ Jul 24 2011, 01:05 AM) Sea $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaaaaa!37C0!<br />\[{a_1}\]$ el primer termino de la P.A y sea d la diferencia de la P.A La suma de los primeros q terminos es $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaakiaacIcacaWGXbGaeyOeI0IaaGOmaiaacMca<br />% cqGHRaWkcaWGKbGaaiikaiaadghacqGHsislcaaIXaGaaiykaiabg2<br />% da9iaadchaaaa!437F!<br />\[{a_1}(q - 2) + d(q - 1) = p\]$ La suma de los primeros p terminos es $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa<br />% aaleaacaaIXaaabeaakiaacIcacaWGWbGaeyOeI0IaaGOmaiaacMca<br />% cqGHRaWkcaWGKbGaaiikaiaadchacqGHsislcaaIXaGaaiykaiabg2<br />% da9iaadghaaaa!437E!<br />\[{a_1}(p - 2) + d(p - 1) = q\]$ Por lo tanto $TEX: % MathType!MTEF!2!1!+-<br />% feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgU<br />% caRiaadghacqGH9aqpcaWGHbWaaSbaaSqaaiaaigdaaeqaaOWaamWa<br />% aeaacaWGWbGaey4kaSIaamyCaiabgkHiTiaaisdaaiaawUfacaGLDb<br />% aacqGHRaWkcaWGKbWaamWaaeaacaWGWbGaey4kaSIaamyCaiabgkHi<br />% TiaaikdacaGGPaaacaGLBbGaayzxaaaaaa!4AE7!<br />\[p + q = {a_1}\left[ {p + q - 4} \right] + d\left[ {p + q - 2)} \right]\]$ Espero respuesta. $TEX: Incorrecto, siga participando. Salu2.$ -------------------- $TEX: Suerte y Éxito. Nos vemos.$

kkcoro3 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 31 2011, 06:15 AM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 354 Registrado: 2-April 11 Desde: Temuco Miembro Nº: 86.120 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Saludos. ¿Se pudo?$ -------------------- $TEX: Suerte y Éxito. Nos vemos.$

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 31 2011, 01:14 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	ya estaba, propuesto por xdanielx y originalmente sacado del Hall&Knight Higher Algebra -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

el_troncoso Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 31 2011, 02:42 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 537 Registrado: 13-June 10 Desde: Linares Miembro Nº: 72.473 Nacionalidad: Sexo:	$TEX: <br />\begin{align}<br /> & \sum\limits_{i=1}^{p+q}{a_{i}=\frac{(p+q)(a_{1}+a_{p+q})}{2}}=\frac{(p+q)(2a_{1}+(p+q-1)d)}{2} \\ <br /> & \text{de donde desconocemos }a_{1}\text{ y }d,\text{pero del problema sabemos:} \\ <br /> & \sum\limits_{i=1}^{p}{a_{i}=\frac{p(a_{1}+a_{p})}{2}}=q \\ <br /> & \sum\limits_{i=1}^{q}{a_{i}=\frac{q(a_{1}+a_{q})}{2}}=p \\ <br /> & \text{tambien podemos deducir:} \\ <br /> & a_{p}=a_{1}+(p-1)d \\ <br /> & a_{q}=a_{1}+(q-1)d \\ <br /> & \text{de donde tenemos 4 ecuaciones y 4 incognitas(}a_{p},a_{q},a_{1}\text{ y }d) \\ <br />\end{align}$ si voy mal me dicen! me da flojerita ahora resolver el sistema ... -------------------- Recopilación Propuestos PSU 2011 Desafío PSU 2011 Derivadas de la forma $TEX: $$f(x)=g(x)^{h(x)}$$$ --> AQUÍ CITA "...La vida de investigacion no es tener LA idea y ganarse un Nobel, es una vida de dedicacion y hacer las cosas por gusto y realizacion personal, no por ganar determinado premio y quedar bien frente a todos. Los premios no son malos, obviamente, pero si esa es tu unica motivacion entonces vas a tener una carrera muy triste. (...) La cosa no funciona asi, la ciencia es una enorme selva desconocida y nosotros solo somos humildes exploradores que caemos en la mitad de ella sin un rumbo claro. Uno explora, y reporta lo que encuentra. Te puede gustar un area determinada, si, pero uno nunca sabe de antemano con que cosa te vas a encontrar. Solo exploramos y reportamos, no andamos buscando desesperadamente un descubrimiento genial que nos lleve al Nobel. Pasten

tochalo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 31 2011, 03:53 PM Publicado: #9
Dios Matemático Grupo: Usuario FMAT Mensajes: 426 Registrado: 13-January 08 Desde: desde la pieza de tu hermana Miembro Nº: 14.612 Nacionalidad: Colegio/Liceo: Sexo:	CITA(el_troncoso @ Jul 31 2011, 04:42 PM) $TEX: <br />\begin{align}<br /> & \sum\limits_{i=1}^{p+q}{a_{i}=\frac{(p+q)(a_{1}+a_{p+q})}{2}}=\frac{(p+q)(2a_{1}+(p+q-1)d)}{2} \\ <br /> & \text{de donde desconocemos }a_{1}\text{ y }d,\text{pero del problema sabemos:} \\ <br /> & \sum\limits_{i=1}^{p}{a_{i}=\frac{p(a_{1}+a_{p})}{2}}=q \\ <br /> & \sum\limits_{i=1}^{q}{a_{i}=\frac{q(a_{1}+a_{q})}{2}}=p \\ <br /> & \text{tambien podemos deducir:} \\ <br /> & a_{p}=a_{1}+(p-1)d \\ <br /> & a_{q}=a_{1}+(q-1)d \\ <br /> & \text{de donde tenemos 4 ecuaciones y 4 incognitas(}a_{p},a_{q},a_{1}\text{ y }d) \\ <br />\end{align}$ si voy mal me dicen! me da flojerita ahora resolver el sistema ... $TEX: <br />\noindent<br />Si, vas bien. Ahora reemplaza $a_P$ y $a_q$ en las respectivas ecuaciones y obtendrás un sistema de 2x2 cuyas incógnitas son $a_1$ y $d$. <br />$ Saludos

el_troncoso Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 31 2011, 11:34 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 537 Registrado: 13-June 10 Desde: Linares Miembro Nº: 72.473 Nacionalidad: Sexo:	CITA(tochalo @ Jul 31 2011, 04:53 PM) $TEX: <br />\noindent<br />Si, vas bien. Ahora reemplaza $a_P$ y $a_q$ en las respectivas ecuaciones y obtendrás un sistema de 2x2 cuyas incógnitas son $a_1$ y $d$. <br />$ Saludos llegué a algo refeo -------------------- Recopilación Propuestos PSU 2011 Desafío PSU 2011 Derivadas de la forma $TEX: $$f(x)=g(x)^{h(x)}$$$ --> AQUÍ CITA "...La vida de investigacion no es tener LA idea y ganarse un Nobel, es una vida de dedicacion y hacer las cosas por gusto y realizacion personal, no por ganar determinado premio y quedar bien frente a todos. Los premios no son malos, obviamente, pero si esa es tu unica motivacion entonces vas a tener una carrera muy triste. (...) La cosa no funciona asi, la ciencia es una enorme selva desconocida y nosotros solo somos humildes exploradores que caemos en la mitad de ella sin un rumbo claro. Uno explora, y reporta lo que encuentra. Te puede gustar un area determinada, si, pero uno nunca sabe de antemano con que cosa te vas a encontrar. Solo exploramos y reportamos, no andamos buscando desesperadamente un descubrimiento genial que nos lleve al Nobel. Pasten

« Posterior · Progresiones: Aritmética y Geométrica · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 05:00 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.