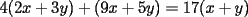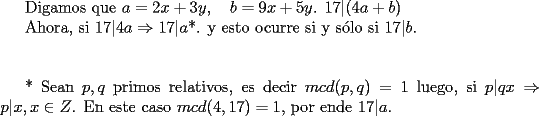|
|
|
|
|
|
|
  |
 Sep 15 2005, 06:28 PM Sep 15 2005, 06:28 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Probar que las expresiones
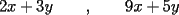  e e 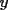 Este es uno de los primeros problemas importantes de saber hacer cuando uno quiere saber un poco mas de disibilidad...veramos como les va a ustedes con este problemita -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
| Corecrasher |
 Sep 15 2005, 08:35 PM Sep 15 2005, 08:35 PM
Publicado:
#2
|
|
Invitado |
Notemos que
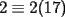 y que y que 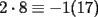 y -1 por impar siempre es -1 , osea y -1 por impar siempre es -1 , osea 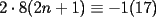 siempre. A su vez siempre. A su vez 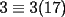 y y 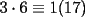 , o sea , o sea 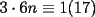 sumando los restos sumando los restos 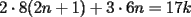 ; por lo cual ; por lo cual 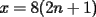 e e 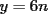 siempre. Ahora bien, siempre. Ahora bien, 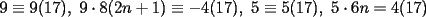 , sumando los restos tenemos que la suma es de la forma , sumando los restos tenemos que la suma es de la forma 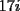 , probando lo pedido. , probando lo pedido.
|
|
|
|
 Sep 23 2005, 11:40 PM Sep 23 2005, 11:40 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
No comprendo esta solución. Esto quiere decir que está mala, o bien que no te expresaste muy bien, dando a entender tus ideas de una forma que no es muy clara. En algún momento sacaste de la manga, el hecho (rotundamente falso) que
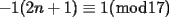 , y me parece que trabajaste con ideas de ese tipo, todo el tiempo. Por lo menos, esto requiere una revisión, para modificar la respuesta, o bien para expresarla en términos claros. , y me parece que trabajaste con ideas de ese tipo, todo el tiempo. Por lo menos, esto requiere una revisión, para modificar la respuesta, o bien para expresarla en términos claros.
-------------------- |
|
|
|
| Corecrasher |
 Oct 20 2005, 09:22 PM Oct 20 2005, 09:22 PM
Publicado:
#4
|
|
Invitado |
Pensemoslo de este modo:
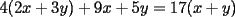 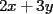 es divisible por 17 lo que implica que es divisible por 17 lo que implica que 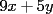 tambien lo sea ya que 4 es coprimo con 17, viceversa lo mismo tambien lo sea ya que 4 es coprimo con 17, viceversa lo mismo |
|
|
|
 Oct 22 2005, 10:39 PM Oct 22 2005, 10:39 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución ahora sí está un poco más cerca de ser algo correcto. Me parece que la acotación "4 es coprimo con 17", está mal posicionada.
Para ser más claro, quieres demostrar una proposición del tipo si y sólo si... explicaste un sentido, donde no hacía falta dicha acotación. Para la otra sí hace falta. O sea debería concluirse con "y viceversa lo mismo, porque 4 es coprimo con 17" ¿Me explico? De todos modos es sólo afinar detalles. Lo otro sería derechamente aprender a redactar una solución -------------------- |
|
|
|
 Feb 19 2006, 09:55 AM Feb 19 2006, 09:55 AM
Publicado:
#6
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Bueno, hacemos un llamado a fundamentar bien este problemita....de tal manera que podamos pasarlo a problemas resueltos(ya lleva mucho tiempo sin una justificacion completa)
Solamente sabiendo interpretar correctamente que: 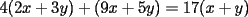 es posible finiquitar el problema...asi que esperamos soluciones -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 7 2007, 10:26 PM Aug 7 2007, 10:26 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- Comienza a crear documentos con LaTeX.
Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería |
|
|
|
 Aug 14 2007, 03:20 PM Aug 14 2007, 03:20 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Aún no tenemos una solución correcta... ciertamente, el problema es simple (para quien entiende ciertas ideas de uso común en Teoría de Números), pero debe explicarse lo necesario el paso importante (si 17 | 4a, entonces 17 | a)
Saludos -------------------- |
|
|
|
 Sep 9 2007, 07:37 PM Sep 9 2007, 07:37 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
hola
Digamos que para ciertos valores de 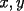 , , 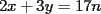 Supongamos que 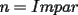 , entonces, como , entonces, como 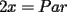 , , 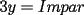 , para conservar la Paridad ( gracias xsebastian , para conservar la Paridad ( gracias xsebastian Ahora si 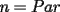 , entonces , por la misma razón anterior, , entonces , por la misma razón anterior, 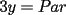 . .Hay que notar que en ambos casos, la paridad de 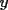 y la paridad de y la paridad de  es la misma. es la misma.Como 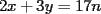 , concluimos que , concluimos que 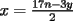 . .Reemplazando en la segunda expresión : 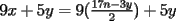 lo que equivale a: lo que equivale a: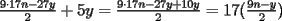 Como hemos dicho al inicio,  e e 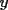 poseen la misma paridad, y ya que cuando sumamos o restamos numeros de la misma paridad, obtenemos un par, que al ser dividido en 2, se obtiene un número entero, concluimos que poseen la misma paridad, y ya que cuando sumamos o restamos numeros de la misma paridad, obtenemos un par, que al ser dividido en 2, se obtiene un número entero, concluimos que 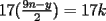 con con 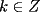 , probando que ambas expresiones son divisibles en 17 para los mismos valores de , probando que ambas expresiones son divisibles en 17 para los mismos valores de 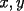 . .
--------------------  |
|
|
|
 Oct 19 2007, 01:32 PM Oct 19 2007, 01:32 PM
Publicado:
#10
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 329 Registrado: 24-August 06 Desde: Concepción Miembro Nº: 2.038 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Veamos si está correcto:
Tenemos, como dijo Kenshin: 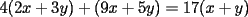 Tomemos un par de enteros (x,y) tal que 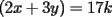 (k es entero) (k es entero)Luego: 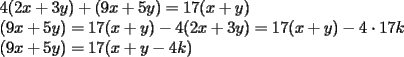 Por lo tanto 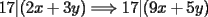 La implicancia también es cierta en sentido opuesto, la demostración es análoga a la ya presentada. Así llegamos a: 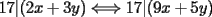 Con lo que demostramos lo pedido. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 09:48 AM |