FMAT Integral Bee! - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Cálculo > Integrales

14 Páginas:

< 1 2 3 4 5 > »

Closed Topic

Start new topic

FMAT Integral Bee!

7words Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 17 2011, 09:08 PM Publicado: #21
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.756 Registrado: 16-September 07 Desde: al frente del Express Miembro Nº: 10.238 Nacionalidad: Universidad: Sexo:	$TEX: \[\int_{ - \infty }^\infty {\frac{{\cos \left( x \right)}}<br />{{{e^x} + {e^{ - x}}}}dx} = \int_{ - \infty }^\infty {\frac{{{e^x}\cos \left( x \right)}}<br />{{{e^{2x}} + 1}}dx} = \operatorname{Re} \left\{ {\int_{ - \infty }^\infty {\frac{{{e^{x\left( {1 + i} \right)}}}}<br />{{{e^{2x}} + 1}}dx} } \right\}\]<br />$ pero: $TEX: \[\int_{ - \infty }^\infty {\frac{{{e^{x\left( {1 + i} \right)}}}}<br />{{{e^{2x}} + 1}}dx} \underbrace = _{x = \log \left( u \right)}\int_0^\infty {\frac{{{u^i}}}<br />{{{u^2} + 1}}du} \]<br />$ Usando la transformada de Mellin,tenemos que: $TEX: \[\int_0^\infty {\frac{{{u^i}}}<br />{{{u^2} + 1}}du = - \frac{{\pi {e^{ - i\pi \left( {1 + i} \right)}}}}<br />{{sen\left( {\pi \left( {1 + i} \right)} \right)}}} \left[ {res\left( {\frac{{{z^i}}}<br />{{{z^2} + 1}}, \pm i} \right)} \right] = \frac{{\pi {e^{ - i\pi \left( {1 + i} \right)}}}}<br />{{sen\left( {\pi \left( {2 + i} \right)} \right)}}\left( {\frac{{{{\left( { \pm i} \right)}^i}}}<br />{{ \pm 2i}}} \right)\]$ $TEX: \[\int_0^\infty {\frac{{{u^{1 + i}}}}<br />{{{u^2} + 1}}du} = \frac{{\pi {e^{ - i\pi \left( {1 + i} \right)}}}}<br />{{sen\left( {\pi \left( {1 + i} \right)} \right)}}\left[ { - \frac{1}<br />{2}{e^{i\pi \left( {1 + i} \right)}}\cos \left( {\frac{{\pi \left( {1 + i} \right)}}<br />{2}} \right)} \right] = \frac{\pi }<br />{2}\sec \left( {\frac{\pi }<br />{2}i} \right)\]$ $TEX: \[Luego:\int_{ - \infty }^\infty {\frac{{\cos \left( x \right)}}<br />{{{e^x} + {e^{ - x}}}}dx} = \operatorname{Re} \left\{ {\int_0^\infty {\frac{{{u^i}}}<br />{{{u^2} + 1}}du} } \right\} = 0\]$ -------------------- Ahora van quedando en el foro solo los niñitos tontitos graves, que lata... u.u

Gastón Burrull	Jun 17 2011, 09:22 PM Publicado: #22
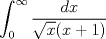
Invitado	Como 7 dejó libre el cupo, propongo: $TEX: $$\int_0^{\infty} \frac{dx}{\sqrt{x}(x+1)}$$$ Mensaje modificado por Gastón Burrull el Jun 17 2011, 09:22 PM

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 17 2011, 09:31 PM Publicado: #23
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	La respuesta de 7words no es correcta. Gastón Burrull, trata de ver otro problema, porque ese es fácil, sale con un cambio de variable y sería.

nmg1302 Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 17 2011, 09:33 PM Publicado: #24
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 832 Registrado: 11-September 07 Desde: París, Francia Miembro Nº: 10.056 Nacionalidad: Sexo:	CITA(7words @ Jun 17 2011, 10:08 PM) $TEX: \[\int_{ - \infty }^\infty {\frac{{\cos \left( x \right)}}<br />{{{e^x} + {e^{ - x}}}}dx} = \int_{ - \infty }^\infty {\frac{{{e^x}\cos \left( x \right)}}<br />{{{e^{2x}} + 1}}dx} = \operatorname{Re} \left\{ {\int_{ - \infty }^\infty {\frac{{{e^{x\left( {1 + i} \right)}}}}<br />{{{e^{2x}} + 1}}dx} } \right\}\]<br />$ pero: $TEX: \[\int_{ - \infty }^\infty {\frac{{{e^{x\left( {1 + i} \right)}}}}<br />{{{e^{2x}} + 1}}dx} \underbrace = _{x = \log \left( u \right)}\int_0^\infty {\frac{{{u^i}}}<br />{{{u^2} + 1}}du} \]<br />$ Usando la transformada de Mellin,tenemos que: $TEX: \[\int_0^\infty {\frac{{{u^i}}}<br />{{{u^2} + 1}}du = - \frac{{\pi {e^{ - i\pi \left( {1 + i} \right)}}}}<br />{{sen\left( {\pi \left( {1 + i} \right)} \right)}}} \left[ {res\left( {\frac{{{z^i}}}<br />{{{z^2} + 1}}, \pm i} \right)} \right] = \frac{{\pi {e^{ - i\pi \left( {1 + i} \right)}}}}<br />{{sen\left( {\pi \left( {2 + i} \right)} \right)}}\left( {\frac{{{{\left( { \pm i} \right)}^i}}}<br />{{ \pm 2i}}} \right)\]$ $TEX: \[\int_0^\infty {\frac{{{u^{1 + i}}}}<br />{{{u^2} + 1}}du} = \frac{{\pi {e^{ - i\pi \left( {1 + i} \right)}}}}<br />{{sen\left( {\pi \left( {1 + i} \right)} \right)}}\left[ { - \frac{1}<br />{2}{e^{i\pi \left( {1 + i} \right)}}\cos \left( {\frac{{\pi \left( {1 + i} \right)}}<br />{2}} \right)} \right] = \frac{\pi }<br />{2}\sec \left( {\frac{\pi }<br />{2}i} \right)\]$ $TEX: \[Luego:\int_{ - \infty }^\infty {\frac{{\cos \left( x \right)}}<br />{{{e^x} + {e^{ - x}}}}dx} = \operatorname{Re} \left\{ {\int_0^\infty {\frac{{{u^i}}}<br />{{{u^2} + 1}}du} } \right\} = 0\]$ resultado incorrecto 7words(no se si con el pozo te referías a eso) aunque no conozco la transformada de mellin como para ver que esta mal

7words Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 17 2011, 09:37 PM Publicado: #25
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.756 Registrado: 16-September 07 Desde: al frente del Express Miembro Nº: 10.238 Nacionalidad: Universidad: Sexo:	CITA(nmg1302 @ Jun 17 2011, 10:33 PM) resultado incorrecto 7words(no se si con el pozo te referías a eso) aunque no conozco la transformada de mellin como para ver que esta mal ahahahhaha qeria probar eso no mas.... lo otro es por que no estaba seguro xd,seguiré intentando. -------------------- Ahora van quedando en el foro solo los niñitos tontitos graves, que lata... u.u

master_c	Jun 17 2011, 10:30 PM Publicado: #26
Invitado	CITA(Gastón Burrull @ Jun 17 2011, 10:22 PM) Como 7 dejó libre el cupo, propongo: $TEX: $$\int_0^{\infty} \frac{dx}{\sqrt{x}(x+1)}$$$ nisiquiera es necesario un cambio $TEX: $$<br />I = \int_0^{ + \infty } {\frac{{dx}}<br />{{\sqrt x \left( {x + 1} \right)}}} = \int_0^{ + \infty } {\frac{{x^{\frac{1}<br />{2} - 1} }}<br />{{\left( {1 + x} \right)^{\frac{1}<br />{2} + \frac{1}<br />{2}} }}dx} = \beta \left( {\frac{1}<br />{2},\frac{1}<br />{2}} \right) = \pi <br />$$$

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 17 2011, 11:51 PM Publicado: #27
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(7words @ Jun 17 2011, 10:37 PM) ahahahhaha qeria probar eso no mas.... lo otro es por que no estaba seguro xd,seguiré intentando. Mi recomendacion personal es que nunca te metas con cosas no-exponenciales con exponente complejo. Dado que son cosas multivaluadas (y nos vamos a la ce te eme) -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

master_c	Jun 17 2011, 11:56 PM Publicado: #28
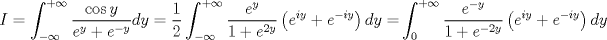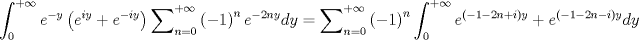Invitado	me falta encontrar la serie y listo $TEX: $$<br />I = \int_{ - \infty }^{ + \infty } {\frac{{\cos y}}<br />{{e^y + e^{ - y} }}dy} = \frac{1}<br />{2}\int_{ - \infty }^{ + \infty } {\frac{{e^y }}<br />{{1 + e^{2y} }}\left( {e^{iy} + e^{ - iy} } \right)dy = } \int_0^{ + \infty } {\frac{{e^{ - y} }}<br />{{1 + e^{ - 2y} }}\left( {e^{iy} + e^{ - iy} } \right)dy} <br />$$$ $TEX: $$<br />\int_0^{ + \infty } {e^{ - y} \left( {e^{iy} + e^{ - iy} } \right)\sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n e^{ - 2ny} } dy} = \sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n \int_0^{ + \infty } {e^{\left( { - 1 - 2n + i} \right)y} + e^{\left( { - 1 - 2n - i} \right)y} dy} } <br />$$$ $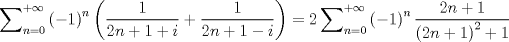TEX: $$<br />\sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n \left( {\frac{1}<br />{{2n + 1 + i}} + \frac{1}<br />{{2n + 1 - i}}} \right) = 2} \sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n \frac{{2n + 1}}<br />{{\left( {2n + 1} \right)^2 + 1}}} <br />$$$

Crash! Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 18 2011, 12:13 AM Publicado: #29
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(master_c @ Jun 18 2011, 12:56 AM) me falta encontrar la serie y listo 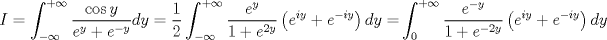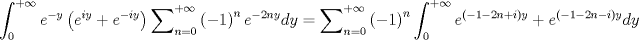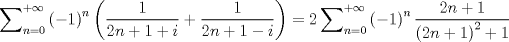$TEX: $$<br />I = \int_{ - \infty }^{ + \infty } {\frac{{\cos y}}<br />{{e^y + e^{ - y} }}dy} = \frac{1}<br />{2}\int_{ - \infty }^{ + \infty } {\frac{{e^y }}<br />{{1 + e^{2y} }}\left( {e^{iy} + e^{ - iy} } \right)dy = } \int_0^{ + \infty } {\frac{{e^{ - y} }}<br />{{1 + e^{ - 2y} }}\left( {e^{iy} + e^{ - iy} } \right)dy} <br />$$$ $TEX: $$<br />\int_0^{ + \infty } {e^{ - y} \left( {e^{iy} + e^{ - iy} } \right)\sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n e^{ - 2ny} } dy} = \sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n \int_0^{ + \infty } {e^{\left( { - 1 - 2n + i} \right)y} + e^{\left( { - 1 - 2n - i} \right)y} dy} } <br />$$$ $TEX: $$<br />\sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n \left( {\frac{1}<br />{{2n + 1 + i}} + \frac{1}<br />{{2n + 1 - i}}} \right) = 2} \sum\nolimits_{n = 0}^{ + \infty } {\left( { - 1} \right)^n \frac{{2n + 1}}<br />{{\left( {2n + 1} \right)^2 + 1}}} <br />$$$ Llegué a la misma serie sin variable compleja $TEX: \[\begin{gathered}<br /> \frac{1}{{1 + {e^{ - 2x}}}} = \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}{e^{ - 2kx}}} \hfill \\<br /> \frac{{{e^x}}}{{{e^x} - {e^{ - x}}}} = \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}{e^{ - 2kx}}} \hfill \\<br /> \Rightarrow \frac{{\cos \left( x \right)}}{{{e^x} - {e^{ - x}}}} = \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}{e^{ - 2kx - x}}\cos \left( x \right)} \hfill \\<br /> \Rightarrow I = 2\int\limits_0^\infty {\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}{e^{ - 2kx - x}}\cos \left( x \right)} dx} \hfill \\<br /> I = 2\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}\int\limits_0^\infty {{e^{ - \left( {2k + 1} \right)x}}\cos \left( x \right)dx} } \hfill \\<br /> I = 2\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}L\left\{ {\cos \left( x \right)} \right\}\left( {2k + 1} \right)} \hfill \\<br /> I = 2\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}\frac{{2k + 1}}{{{{\left( {2k + 1} \right)}^2} + 1}}} \hfill \\ <br />\end{gathered} \]$ -------------------- Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed.

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 18 2011, 12:13 AM Publicado: #30
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Yo creo que con residuos demas que sale --------------------

« Posterior · Integrales · Anterior »

14 Páginas:

< 1 2 3 4 5 > »

Closed Topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 11:01 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.