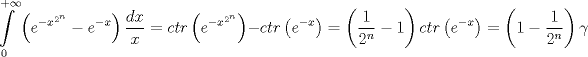FMAT Integral Bee! - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Cálculo > Integrales

14 Páginas:

« < 11 12 13 14 >

FMAT Integral Bee!

Opciones

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 3 2011, 04:54 PM Publicado: #121
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(danielxbeats @ Aug 3 2011, 05:13 PM) solo qedaria analizar el caso a = 1 pues claramente se indetermina con la solucion anterior 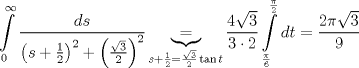$TEX: $$<br />\int\limits_{0}^{\infty }{\frac{ds}{\left( s+\frac{1}{2} \right)^{2}+\left( \frac{\sqrt{3}}{2} \right)^{2}}}\underbrace{=}_{s+\frac{1}{2}=\frac{\sqrt{3}}{2}\tan t}\frac{4\sqrt{3}}{3\cdot 2}\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}}{dt}=\frac{2\pi \sqrt{3}}{9}$$<br />$ --------------------

master_c	Aug 6 2011, 04:05 PM Publicado: #122
Invitado	danielomalmsteen te toca proponer .

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 6 2011, 07:29 PM Publicado: #123
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(master_c @ Aug 6 2011, 05:05 PM) danielomalmsteen te toca proponer . Me da japita vivancooo xd Propon una tuu pooo....una pica a SOS xD --------------------

master_c	Aug 6 2011, 07:41 PM Publicado: #124
Invitado	wusajkjksakj dale, propongo si n natural 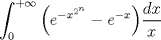$TEX: $$<br />\int_0^{ + \infty } {\left( {e^{ - x^{2^n } } - e^{ - x} } \right)} \frac{{dx}}<br />{x}<br />$$$

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 6 2011, 08:59 PM Publicado: #125
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(master_c @ Aug 6 2011, 08:41 PM) wusajkjksakj dale, propongo si n natural $TEX: $$<br />\int_0^{ + \infty } {\left( {e^{ - x^{2^n } } - e^{ - x} } \right)} \frac{{dx}}<br />{x}<br />$$$ Consideramos 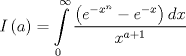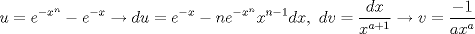$TEX: $$<br />I\left( a \right)=\int\limits_{0}^{\infty }{\frac{\left( e^{-x^{n}}-e^{-x} \right)dx}{x^{a+1}}}<br />$$$ $TEX: $$<br />u=e^{-x^{n}}-e^{-x}\to du=e^{-x}-ne^{-x^{n}}x^{n-1}dx,\text{ }dv=\frac{dx}{x^{a+1}}\to v=\frac{-1}{ax^{a}}<br />$$$ Luego, $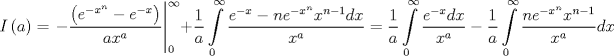TEX: $$<br />I\left( a \right)=\left. 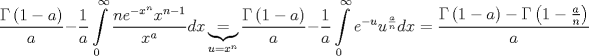-\frac{\left( e^{-x^{n}}-e^{-x} \right)}{ax^{a}} \right\|_{0}^{\infty }+\frac{1}{a}\int\limits_{0}^{\infty }{\frac{e^{-x}-ne^{-x^{n}}x^{n-1}dx}{x^{a}}}=\frac{1}{a}\int\limits_{0}^{\infty }{\frac{e^{-x}dx}{x^{a}}-\frac{1}{a}\int\limits_{0}^{\infty }{\frac{ne^{-x^{n}}x^{n-1}}{x^{a}}}dx}<br />$$$ $TEX: $$<br />\frac{\Gamma \left( 1-a \right)}{a}-\frac{1}{a}\int\limits_{0}^{\infty }{\frac{ne^{-x^{n}}x^{n-1}}{x^{a}}}dx\underbrace{=}_{u=x^{n}}\frac{\Gamma \left( 1-a \right)}{a}-\frac{1}{a}\int\limits_{0}^{\infty }{e^{-u}u^{\frac{a}{n}}}dx=\frac{\Gamma \left( 1-a \right)-\Gamma \left( 1-\frac{a}{n} \right)}{a}<br />$$$ Ahora para evaluar en cero, tomamos Limite y aplicamos LH! xd 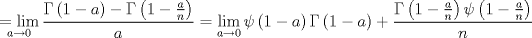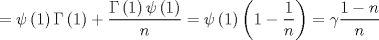$TEX: $$<br />\underset{a\to 0}{\mathop{=\lim }}\,\frac{\Gamma \left( 1-a \right)-\Gamma \left( 1-\frac{a}{n} \right)}{a}=\underset{a\to 0}{\mathop{\lim }}\,\psi \left( 1-a \right)\Gamma \left( 1-a \right)+\frac{\Gamma \left( 1-\frac{a}{n} \right)\psi \left( 1-\frac{a}{n} \right)}{n}<br />$$$ $TEX: $$<br />=\psi \left( 1 \right)\Gamma \left( 1 \right)+\frac{\Gamma \left( 1 \right)\psi \left( 1 \right)}{n}=\psi \left( 1 \right)\left( 1-\frac{1}{n} \right)=\gamma \frac{1-n}{n}<br />$$$ Entonces la integral de Vivanco vale 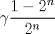$TEX: $$<br />\gamma \frac{1-2^{n}}{2^{n}}<br />$$$ Voi saliendo asi que propongan no maaaaaas xd --------------------

master_c	Aug 6 2011, 09:45 PM Publicado: #126
Invitado	respuesta no correcta xd debe ser con el signo cambiado saludos! Mensaje modificado por master_c el Aug 6 2011, 09:49 PM

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 6 2011, 10:32 PM Publicado: #127
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(master_c @ Aug 6 2011, 10:45 PM) respuesta no correcta xd debe ser con el signo cambiado saludos! Aahhh wnnn es lo de menoss xd, propoongaaaa xD --------------------

master_c	Aug 6 2011, 10:40 PM Publicado: #128
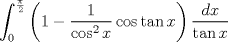Invitado	Calcular $TEX: $$<br />\int_0^{\frac{\pi }<br />{2}} {\left( {1 - \frac{1}<br />{{\cos ^2 x}}\cos \tan x} \right)\frac{{dx}}<br />{{\tan x}}} <br />$$$

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 7 2011, 12:10 AM Publicado: #129
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(master_c @ Aug 6 2011, 10:45 PM) respuesta no correcta xd debe ser con el signo cambiado saludos! 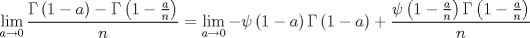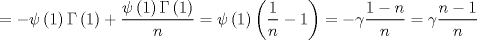$TEX: $$<br />\mathop {\lim }\limits_{a \to 0} \frac{{\Gamma \left( {1 - a} \right) - \Gamma \left( {1 - \frac{a}<br />{n}} \right)}}<br />{n} = \mathop {\lim }\limits_{a \to 0} - \psi \left( {1 - a} \right)\Gamma \left( {1 - a} \right) + \frac{{\psi \left( {1 - \frac{a}<br />{n}} \right)\Gamma \left( {1 - \frac{a}<br />{n}} \right)}}<br />{n}<br />$$<br />$ $TEX: $$<br /> = - \psi \left( 1 \right)\Gamma \left( 1 \right) + \frac{{\psi \left( 1 \right)\Gamma \left( 1 \right)}}<br />{n} = \psi \left( 1 \right)\left( {\frac{1}<br />{n} - 1} \right) = - \gamma \frac{{1 - n}}<br />{n} = \gamma \frac{{n - 1}}<br />{n}<br />$$<br />$ Entonces la integral valee: 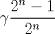$TEX: $$<br />\gamma \frac{{2^n - 1}}<br />{{2^n }}<br />$$<br />$ Mensaje modificado por danielomalmsteen el Aug 7 2011, 12:14 AM --------------------

master_c	Aug 7 2011, 07:42 PM Publicado: #130
Invitado	CITA(danielomalmsteen @ Aug 7 2011, 01:10 AM) $TEX: $$<br />\mathop {\lim }\limits_{a \to 0} \frac{{\Gamma \left( {1 - a} \right) - \Gamma \left( {1 - \frac{a}<br />{n}} \right)}}<br />{n} = \mathop {\lim }\limits_{a \to 0} - \psi \left( {1 - a} \right)\Gamma \left( {1 - a} \right) + \frac{{\psi \left( {1 - \frac{a}<br />{n}} \right)\Gamma \left( {1 - \frac{a}<br />{n}} \right)}}<br />{n}<br />$$<br />$ $TEX: $$<br /> = - \psi \left( 1 \right)\Gamma \left( 1 \right) + \frac{{\psi \left( 1 \right)\Gamma \left( 1 \right)}}<br />{n} = \psi \left( 1 \right)\left( {\frac{1}<br />{n} - 1} \right) = - \gamma \frac{{1 - n}}<br />{n} = \gamma \frac{{n - 1}}<br />{n}<br />$$<br />$ Entonces la integral valee: $TEX: $$<br />\gamma \frac{{2^n - 1}}<br />{{2^n }}<br />$$<br />$ ahora si correcto que alguien se anime a resolver y que propongan saludos! $TEX: $$<br />\int\limits_0^{ + \infty } {\left( {e^{ - x^{2^n } } - e^{ - x} } \right)\frac{{dx}}<br />{x}} = ctr\left( {e^{ - x^{2^n } } } \right) - ctr\left( {e^{ - x} } \right) = \left( {\frac{1}<br />{{2^n }} - 1} \right)ctr\left( {e^{ - x} } \right) = \left( {1 - \frac{1}<br />{{2^n }}} \right)\gamma <br />$$$ Mensaje modificado por master_c el Aug 7 2011, 09:55 PM

« Posterior · Integrales · Anterior »

14 Páginas:

« < 11 12 13 14 >

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 11:55 PM