|
|
|
|
|
|
|
  |
 Jun 16 2011, 10:28 PM Jun 16 2011, 10:28 PM
Publicado:
#1
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Esto funciona de la siguiente manera: se empieza dando una integral para resolver. Si se tiene una respuesta completa y correcta, se postea, de lo contrario no posteen.
Se postea la solución y en el mismo post, la integral para que otros la resuelvan. Si nadie resuelve la integral durante 48 horas, que no es muy probable, el que la propuso ha de resolverla y de nuevo será el turno para desafiarnos con un problema nuevo. Cualquiera puede participar, e incluso se pueden postear soluciones alternas a problemas ya resueltos. (Para esto citen el problema para mantener el orden.) Finalmente, asegúrense de que su problema sea interesante, con resultado elemental y que tampoco sea muy fácil de resolver, ni mucho menos den un Hint!!! (Pueden asumir resultados clásicos para ser aplicados a la resolución de cualquier problema.) Partimos: Evaluar 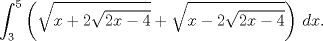
|
|
|
|
 Jun 16 2011, 10:46 PM Jun 16 2011, 10:46 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 541 Registrado: 31-May 08 Desde: 33º28'32'' S 70º34'57'' W Miembro Nº: 25.337 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Evaluar 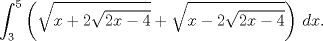  Ahora propongo el mio. 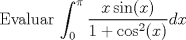 EDIT: 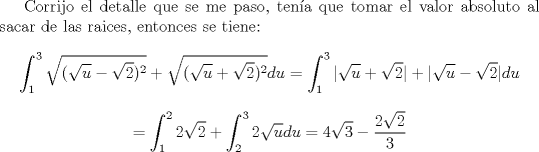
Mensaje modificado por NickdrA el Jun 16 2011, 10:59 PM --------------------  Recopilación de posts notables para todos los gustos: |
|
|
|
 Jun 16 2011, 10:51 PM Jun 16 2011, 10:51 PM
Publicado:
#3
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
NickdrA, el resultado no es correcto, revísalo.
|
|
|
|
 Jun 16 2011, 11:04 PM Jun 16 2011, 11:04 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
[quote name='NickdrA' date='Jun 16 2011, 11:46 PM' post='534517']
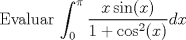 ![TEX: \[\begin{gathered}<br /> I = \int\limits_0^\pi {\frac{{x\sin xdx}}<br />{{1 + {{\cos }^2}x}}} \underbrace = _{x \to \pi - x} - \int\limits_\pi ^0 {\frac{{\left( {\pi - x} \right)\sin xdx}}<br />{{1 + {{\cos }^2}x}}} = \pi \int\limits_0^\pi {\frac{{\sin xdx}}<br />{{1 + {{\cos }^2}x}}} - I \hfill \\<br /> \hfill \\<br /> 2I = \pi \int\limits_0^\pi {\frac{{\sin xdx}}<br />{{1 + {{\cos }^2}x}}} \underbrace = _{u = \cos x}\pi \int\limits_{ - 1}^1 {\frac{{du}}<br />{{1 + {u^2}}}} = \pi \left( {\arctan \left( 1 \right) - \arctan \left( { - 1} \right)} \right) = \frac{{{\pi ^2}}}<br />{2} \hfill \\<br /> \hfill \\<br /> \to I = \frac{{{\pi ^2}}}<br />{4} \hfill \\ <br />\end{gathered} \]<br />](/tex-image/ea3d3b1fe611d76d55c7dab59ec69d24.png) Propongo: ![TEX: \[\int\limits_0^1 {\frac{{\ln xdx}}<br />{{1 + {x^2}}}} \]<br />](/tex-image/cec3d782b447ffd55a922303b6d17163.png)
--------------------  |
|
|
|
 Jun 16 2011, 11:05 PM Jun 16 2011, 11:05 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: \[\begin{gathered}<br /> {\text{hacemos la sustitucion }}t = \pi - x \hfill \\<br /> I = \int\limits_0^\pi {\frac{{\left( {\pi - t} \right)\sin \left( t \right)}}{{1 + {{\cos }^2}\left( t \right)}}dt} = \pi \int\limits_0^\pi {\frac{{\sin \left( t \right)}}{{1 + {{\cos }^2}\left( t \right)}}dt} - I \hfill \\<br /> 2I = \pi \arctan \left( {\cos \left( t \right)} \right)_\pi ^0 = 2\pi \arctan \left( 1 \right) \hfill \\<br /> I = \frac{{{\pi ^2}}}{4} \hfill \\<br /> \hfill \\<br /> {\text{Evaluar}} \hfill \\<br /> \int\limits_0^{\frac{\pi }{2}} {\sqrt {\cot \left( x \right)} dx} \hfill \\ <br />\end{gathered} \]](/tex-image/cb8fb5d8b846541e49d381bc53103e51.png) me ganaste ¬¬ Mensaje modificado por Crash! el Jun 16 2011, 11:05 PM --------------------  Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed. |
|
|
|
 Jun 16 2011, 11:18 PM Jun 16 2011, 11:18 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
--------------------  |
|
|
|
 Jun 16 2011, 11:25 PM Jun 16 2011, 11:25 PM
Publicado:
#7
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
No se desordenen, este fue el problema que había de ser resuelto:
![TEX: \[\int\limits_0^1 {\frac{{\ln xdx}}<br />{{1 + {x^2}}}} \]<br />](/tex-image/cec3d782b447ffd55a922303b6d17163.png) 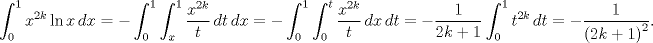 Entonces, 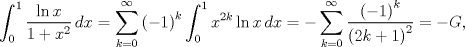 donde donde 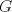 es la constante de Catalán. es la constante de Catalán.
|
|
|
|
 Jun 16 2011, 11:29 PM Jun 16 2011, 11:29 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 929 Registrado: 22-June 08 Desde: Santiago Miembro Nº: 27.979 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: \[\begin{gathered}<br /> sea \hfill \\<br /> I = \int\limits_0^1 {\frac{{\ln \left( {1 + x} \right)}}{x}dx} \hfill \\<br /> como\;\frac{1}{{1 + x}} = \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}{x^k}} \hfill \\<br /> I = \int\limits_0^1 {\sum\limits_{k = 0}^\infty {\frac{{{{\left( { - 1} \right)}^k}{x^k}}}{{k + 1}}} dx} = \sum\limits_{k = 0}^\infty {\frac{{{{\left( { - 1} \right)}^k}}}{{{{\left( {k + 1} \right)}^2}}}} = \sum\limits_{k = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{k + 1}}}}{{{k^2}}}} = \frac{{{\pi ^2}}}{{12}} \hfill \\ <br />\end{gathered} \]](/tex-image/94b59ee14aac1034070deff377d7c2a4.png) ![TEX: \[\int\limits_0^\infty {\frac{{\cos \left( x \right) - 1}}{{{x^2}}}dx} \]](/tex-image/2ccd516986b314532d59cd9ca7e36a19.png)
Mensaje modificado por Crash! el Jun 16 2011, 11:39 PM --------------------  Ex-Electrico Usach 2008 Mechón Injenieria 2009 Tengo Sed. |
|
|
|
 Jun 17 2011, 12:10 AM Jun 17 2011, 12:10 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: \[\begin{gathered}<br /> sea \hfill \\<br /> I = \int\limits_0^1 {\frac{{\ln \left( {1 + x} \right)}}{x}dx} \hfill \\<br /> como\;\frac{1}{{1 + x}} = \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}{x^k}} \hfill \\<br /> I = \int\limits_0^1 {\sum\limits_{k = 0}^\infty {\frac{{{{\left( { - 1} \right)}^k}{x^k}}}{{k + 1}}} dx} = \sum\limits_{k = 0}^\infty {\frac{{{{\left( { - 1} \right)}^k}}}{{{{\left( {k + 1} \right)}^2}}}} = \sum\limits_{k = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{k + 1}}}}{{{k^2}}}} = \frac{{{\pi ^2}}}{{12}} \hfill \\ <br />\end{gathered} \]](/tex-image/94b59ee14aac1034070deff377d7c2a4.png) ![TEX: \[\int\limits_0^\infty {\frac{{\cos \left( x \right) - 1}}{{{x^2}}}dx} \]](/tex-image/2ccd516986b314532d59cd9ca7e36a19.png) ![TEX: \[\begin{gathered}<br /> I\left( u \right) = \int\limits_0^\infty {\frac{{\cos \left( {ux} \right) - 1}}<br />{{{x^2}}}dx} \to I'\left( u \right) = - \int\limits_0^\infty {\frac{{\sin \left( {ux} \right)}}<br />{x}dx} = - \frac{\pi }<br />{2} \hfill \\<br /> \hfill \\<br /> \to I'\left( u \right) = - \frac{\pi }<br />{2} \to I\left( u \right) = - \frac{{\pi u}}<br />{2} + C \hfill \\<br /> \hfill \\<br /> I\left( 0 \right) = 0 \to C = 0 \hfill \\<br /> \hfill \\<br /> \therefore I\left( 1 \right) = - \frac{\pi }<br />{2} \hfill \\ <br />\end{gathered} \]<br />](/tex-image/7be9ece2cf9c3f6d7b6fb678c4cd602e.png) Propongo: ![TEX: \[\int\limits_0^1 {\frac{{\ln x}}<br />{{\sqrt x }}dx} \]<br />](/tex-image/9425c1afe98118e0ab4050111c0707eb.png) cambiada a pedido del publico xD cambiada a pedido del publico xD
Mensaje modificado por danielomalmsteen el Jun 17 2011, 12:33 AM --------------------  |
|
|
|
 Jun 17 2011, 12:25 AM Jun 17 2011, 12:25 AM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ta muy Paja? xDD
Edit:ahi la cambie xd Mensaje modificado por danielomalmsteen el Jun 17 2011, 12:33 AM --------------------  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:55 PM |















![TEX: \[\begin{gathered}<br /> I = \int\limits_0^{\frac{\pi }<br />{2}} {\sqrt {\cot x} dx} = \int\limits_0^{\frac{\pi }<br />{2}} {{{\cos }^{2\left( {\frac{3}<br />{4}} \right) - 1}}x \cdot {{\sin }^{2\left( {\frac{1}<br />{4}} \right) - 1}}xdx} = \frac{1}<br />{2}{\rm B}\left( {\frac{3}<br />{4}} \right){\rm B}\left( {\frac{1}<br />{4}} \right) \hfill \\<br /> \hfill \\<br /> = \frac{1}<br />{2}\frac{\pi }<br />{{\sin \left( {\frac{\pi }<br />{4}} \right)}} = \frac{\pi }<br />{{\sqrt 2 }} \hfill \\ <br />\end{gathered} \]<br />](/tex-image/e956aa106a0580002db6f63889df99da.png)
![TEX: \[\int\limits_0^1 {\frac{{\ln \left( {1 + x} \right)dx}}<br />{x}} \]<br />](/tex-image/d2c0b26fc113a94bc1bb43cb3e79d127.png)