|
|
|
|
|
|
|
  |
 Nov 21 2005, 10:18 PM Nov 21 2005, 10:18 PM
Publicado:
#41
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(DarkBlader @ Nov 21 2005, 11:02 PM) la solu del problema 8: Como tengo 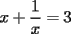 , si lo elevo al cubo, apareceran los terminos ke ando buscando. Para poder realizar la ecuacion, necesitare la piramide de pascal, y como la tercera linea de la piramide corresponde a un binomio elevado al cubo, diremos lo siguiente: , si lo elevo al cubo, apareceran los terminos ke ando buscando. Para poder realizar la ecuacion, necesitare la piramide de pascal, y como la tercera linea de la piramide corresponde a un binomio elevado al cubo, diremos lo siguiente: 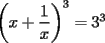 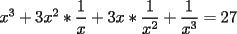 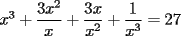 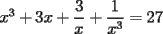 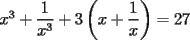 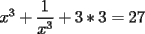 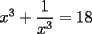 ... porque el 9 pasó restando al 27. ... porque el 9 pasó restando al 27. Solucion Impecable....el problema ya estaba resuelto en la primera hoja pero vale porque la solucion es diferente PD:La explicacion del problema de congruencia aun no me queda muy muy clara..creo que el argumento es super directo con congruencia y de verdad te recomiendo tratar de descubrir la propiedad que te recomendaba(o bien trata de explicarme con ejemplos lo que estabas tratando de decir,pero ejemplos que abarquen cualquier caso..o sea tu debes de asegurarme que tu argumento siempre es valido y no solo para el ejemplo que tu propones Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
| kata |
 Dec 14 2005, 11:00 AM Dec 14 2005, 11:00 AM
Publicado:
#42
|
|
Invitado |
p1: si se dice q hay
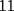 numero de numero de y se pueden hacer operaciones tomando y se pueden hacer operaciones tomando  de estos numero sumarle o retarles o en conjunto lo mas logico de pensar si son once no se podran tener de estos numero sumarle o retarles o en conjunto lo mas logico de pensar si son once no se podran tener 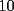 numeos de a once ya que el once es impar numeos de a once ya que el once es impar pero si se ´puede llegar a 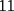 numero de numero de 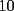 x ej si tenemos  (impar al = q el 11) numeros de a uno y llegar a (impar al = q el 11) numeros de a uno y llegar a 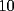 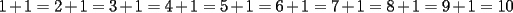 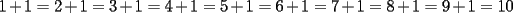 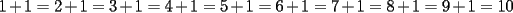 creo q estaa bien noc :S bueno grax david x incentivarme a postiar |
|
|
|
| Corecrasher |
 Dec 16 2005, 07:04 PM Dec 16 2005, 07:04 PM
Publicado:
#43
|
|
Invitado |
CITA(kata @ Dec 14 2005, 01:00 PM) p1: si se dice q hay 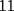 numero de[tex=./tex/19130.gif' alt='TEX: 1'> y se pueden hacer operaciones tomando numero de[tex=./tex/19130.gif' alt='TEX: 1'> y se pueden hacer operaciones tomando  de estos numero sumarle o retarles o en conjunto lo mas logico de pensar si son once no se podran tener de estos numero sumarle o retarles o en conjunto lo mas logico de pensar si son once no se podran tener 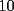 numeos de a once ya que el once es impar numeos de a once ya que el once es impar pero si se ´puede llegar a 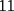 numero de numero de 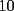 x ej si tenemos  numeros de a uno y llegar a <img src=) 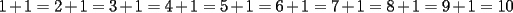 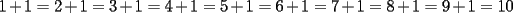 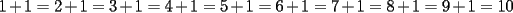 creo q estaa bien noc :S bueno grax david x incentivarme a postiar Kata , primero que nada , mejor registrate , asi tienes muchas mas atribuciones en el foro , pero lo mas importante es que leas esto http://www.fmat.cl/index.php?showtopic=7&view=findpost&p=118 |
|
|
|
 Dec 16 2005, 09:49 PM Dec 16 2005, 09:49 PM
Publicado:
#44
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 21 Registrado: 26-November 05 Desde: Santiagoo Miembro Nº: 420 |
Problema 10)
Bueno, lo que yo hice fue una tabla de doble entrada para ver todas las posibilidades de suma que tenía.. Si se trata de buscar combinaciones en que el resultado de las sumas tengan siempre un numero distinto en las unidades (en este caso del 0 al 9) [Dibujo 1] Por ejemplo: [Dibujo 2] De esta, o cualquier otra forma que elijamos, siempre se repite un número, en este caso nos faltaría un número terminado en 6… y así en todas las combinaciones posibles. De esta forma sería imposible escribir la segunda fila de números de forma que la suma tenga distintos números en la cifra de las unidades.. Eso..
Archivo(s) Adjunto(s)
-------------------- Al regresar verás mi carnaval
And I have honored your request for silence  |
|
|
|
 Dec 29 2005, 09:25 PM Dec 29 2005, 09:25 PM
Publicado:
#45
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Bueno....digamos k no es la forma mas "matemática" de resolver el problema; sin embargo, esa es la forma k podrias resolver el problema en un computador (lo cual no deja de ser interesante). Asi k a seguir haciendo aportes no mas!!!!!!!!
-------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 Jan 4 2006, 01:22 PM Jan 4 2006, 01:22 PM
Publicado:
#46
|
|
 Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 3-January 06 Miembro Nº: 483 |
Respuesta al problema 6:
Todo cuadrado perfecto contiene en su factorización potencias primas pares. Si el entero dado es cuadrado , puesto que tiene 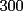 unos, es divisible por tres de acuerdo con la regla de divisibilidad (3|300). Ahora bien, si es divisible por unos, es divisible por tres de acuerdo con la regla de divisibilidad (3|300). Ahora bien, si es divisible por  , y es cuadrado, debe ser divisible por , y es cuadrado, debe ser divisible por  . Pero . Pero 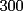 no es divisible por no es divisible por  . Por la regla de divisibilidad por . Por la regla de divisibilidad por  , ,  no es divisible por no es divisible por  . Por tanto, . Por tanto,  no es cuadrado. no es cuadrado.
-------------------- Aestus erat, mediamque dies exegerat horam;
adposui medio membra levanda toro. pars adaperta fuit, pars altera clausa fenestrae; quale fere silvae lumen habere solent, qualia sublucent fugiente crepuscula Phoebo, 5 aut ubi nox abiit, nec tamen orta dies. illa verecundis lux est praebenda puellis, qua timidus latebras speret habere pudor. ecce, Corinna venit, tunica velata recincta, candida dividua colla tegente coma— |
|
|
|
| Corecrasher |
 Jan 4 2006, 10:07 PM Jan 4 2006, 10:07 PM
Publicado:
#47
|
|
Invitado |
CITA(Publius Ovidius Naso @ Jan 4 2006, 03:22 PM) [u]Respuesta al problema 6: Todo cuadrado perfecto contiene en su factorización potencias primas pares. Si el entero dado es cuadrado , puesto que tiene 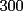 unos, es divisible por tres de acuerdo con la regla de divisibilidad (3|300). Ahora bien, si es divisible por unos, es divisible por tres de acuerdo con la regla de divisibilidad (3|300). Ahora bien, si es divisible por  , y es cuadrado, debe ser divisible por , y es cuadrado, debe ser divisible por  . Pero . Pero 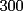 no es divisible por no es divisible por  . Por la regla de divisibilidad por . Por la regla de divisibilidad por  , ,  no es divisible por no es divisible por  . Por tanto, . Por tanto,  no es cuadrado. no es cuadrado.Todos los cuadrados o son divisibles por 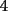 o dejan resto o dejan resto 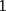 al dividirlos por al dividirlos por 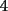 , entonces podemos decir que , entonces podemos decir que 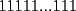  unos no es nunca cuadrado pues si nos fijamos en sus ultimas 2 cifras para usar la regla de divisibilidad por unos no es nunca cuadrado pues si nos fijamos en sus ultimas 2 cifras para usar la regla de divisibilidad por 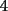 , estas no dejan ni resto , estas no dejan ni resto  ni resto ni resto 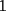 al dividirlos por cuatro , entonces no es cuadrado. Para el caso particular del caso basta con poner al dividirlos por cuatro , entonces no es cuadrado. Para el caso particular del caso basta con poner 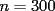
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:53 PM |












