|
|
|
|
|
|
|
  |
 May 29 2005, 04:44 PM May 29 2005, 04:44 PM
Publicado:
#31
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Gracias!! xDDDD
|
|
|
|
 Oct 5 2005, 07:26 PM Oct 5 2005, 07:26 PM
Publicado:
#32
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 129 Registrado: 20-June 05 Desde: Santiago ^^ Miembro Nº: 115 Nacionalidad:  Sexo:  |
P3)En un tablero de 4x4 Pedro y Martín se turnan para colocar ceros o unos en cada casillero. Pedro gana si la suma de los números de alguna fila es impar. De lo contrario gana Martín. Comienza jugando Pedro, ¿quién tiene la estrategia ganadora? Por qué.
La estrategia ganadora la tiene Martín Porque, si Pedro parte, supongamos parte con un 1, luego martín coloca un 1, y Pedro para lograr que sea impar, debe colocar un 1, y martín pondrá un 1, y dará como resultado 4, o sea par Ahora, la clave esta que como martin cierra la fila, lo que podría enfrentar sería lo siguiente;...que ya esten sumado 3, y él pondrá el 1 que falta... ...que sumen 2, y martin pondrá un 0 ...que sumen 1, y martin pondrá un 1 A lo que voy, Dependiendo de como vaya la suma, si es impar, martin pondra un 1, si es par martin pondra un 0... y así siempre logrará que de par Saludos |
|
|
|
 Nov 20 2005, 10:14 AM Nov 20 2005, 10:14 AM
Publicado:
#33
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 116 Registrado: 14-May 05 Desde: Buin, Santiago Miembro Nº: 26 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ahora lo posteo registrado
Ya...hola pos... bueno pase por aca... no habia visto esta sección, y voy a hacer una sol. cortita para el problema 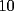 . .El asunto es que en la primera fila, los numeros del 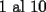 suman suman 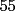 . .En la segunda, tb toos los numeros suman 55. Osea que la primera fila, mas la segunda fila suman 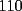 , por lo tanto, la suma de las unidades de la 3ra fila deberia ser , por lo tanto, la suma de las unidades de la 3ra fila deberia ser 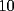 o un multiplo o un multiplo 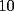 . . Sin embargo, nos damos cuenta que el problema nos dice que en la 3era fila las unidades deberian ser todas distintas, es decir, deberian estar las unidades desde el  hasta el hasta el  (no importa en que orden). Si suman esas unidades solamente, les da (no importa en que orden). Si suman esas unidades solamente, les da 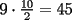 . Y como . Y como 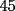 termina en termina en  y no en y no en  , significa que en la segunda fila es imposible que sean todas las unidades distintas, o sea que al menos una se deberia repetir. , significa que en la segunda fila es imposible que sean todas las unidades distintas, o sea que al menos una se deberia repetir.Ya pos...eso sería...chau no mas by 8) Master® --------------------   "Lo que no entiendes hoy lo comprenderás mañana" |
|
|
|
| Michael |
 Nov 20 2005, 01:36 PM Nov 20 2005, 01:36 PM
Publicado:
#34
|
|
Invitado |
en el problema 5 ¿ta bien la solu?
como nos damos cuenta, la suma de los digitos del 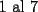 dan dan 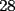 . este resultado da en cualquier caso si se forman . este resultado da en cualquier caso si se forman  numeros con estos digitos, pero ay una exepcion, ke es cuando la suma de dos de las cifras de los dos numeros formados da un numero ke tiene decena y unidad (entre numeros con estos digitos, pero ay una exepcion, ke es cuando la suma de dos de las cifras de los dos numeros formados da un numero ke tiene decena y unidad (entre 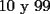 ), aqui pasa ke le tenemos ke restar ), aqui pasa ke le tenemos ke restar 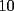 al numero al numero 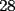 , porke se suprime la decena, que eslo mismo ke restarle , porke se suprime la decena, que eslo mismo ke restarle 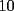 , y luego le sumamos , y luego le sumamos 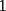 , por la reserva ke pasa por el borrado de la decena del numero anterior, de la sgte,. manera: , por la reserva ke pasa por el borrado de la decena del numero anterior, de la sgte,. manera: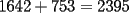 de esta manera cuando el se sumaron el  con el con el  , dio , dio 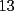 , y aqui se escribio el , y aqui se escribio el  , y se le sumo la reserva al , y se le sumo la reserva al 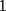 , y como vemos el resultado dio , y como vemos el resultado dio 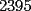 , donde la suma de sus cifras da , donde la suma de sus cifras da 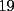 . Con la regla de divisibilidad del . Con la regla de divisibilidad del  , ke dice ke en un numero de , ke dice ke en un numero de  cifras, la suma de esas cifras, la suma de esas  cifras si da multiplo de cifras si da multiplo de  , es divisible por , es divisible por  , y como el , y como el 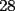 y el y el 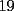 , ke son las posibilidades de las sumas de las cifras del numero ke se forma con los digitos del , ke son las posibilidades de las sumas de las cifras del numero ke se forma con los digitos del  no es multiplo de no es multiplo de  , es imposible la solucion. , es imposible la solucion.responde por fa si esta bueno o no |
|
|
|
| Michael |
 Nov 20 2005, 04:04 PM Nov 20 2005, 04:04 PM
Publicado:
#35
|
|
Invitado |
vamos a decir ke al ke le hicimos el problema penso un numero (n)
el al agregar un  al numero ke penso, es como decir ke al numero ke penso, es como decir ke  es igual al es igual al 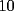 , y al numero ke le agrego el , y al numero ke le agrego el  es es 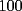 . Si pensamos hay ke restar el . Si pensamos hay ke restar el 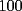 con el con el 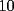 , y esto nos dio , y esto nos dio 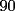 , ke esto es igual a , ke esto es igual a 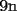 en una expresion algebraica. Luego pensamos ke la suma de las cifras del resultado de la resta es igual a un multiplo de en una expresion algebraica. Luego pensamos ke la suma de las cifras del resultado de la resta es igual a un multiplo de  , y ella al kitarle un digito, ke uede ser hasta , y ella al kitarle un digito, ke uede ser hasta  , sabremos ke le falta una cierta cantidasd para llegar a un multiplo de , sabremos ke le falta una cierta cantidasd para llegar a un multiplo de  mayor ke la suma de las cifras del resultado ke kedo al restarle la cifra. Por ejemplo: Penso el mayor ke la suma de las cifras del resultado ke kedo al restarle la cifra. Por ejemplo: Penso el 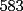 . . 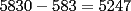 Luego: Luego: 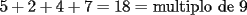 por ejemplo si le borro el 4 kedaria de la siguiente manera: 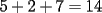 Luego: el multiplo de Luego: el multiplo de  mas cercano y mayor es mas cercano y mayor es 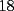 Como a 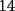 le faltan le faltan 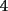 para llegar al para llegar al 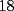 , se sabe ke , se sabe ke 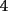 es el digito ke le borro. es el digito ke le borro. |
|
|
|
 Nov 20 2005, 04:17 PM Nov 20 2005, 04:17 PM
Publicado:
#36
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Michael @ Nov 20 2005, 02:36 PM) en el problema 5 ¿ta bien la solu? como nos damos cuenta, la suma de los digitos del 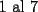 dan dan 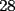 . este resultado da en cualquier caso si se forman . este resultado da en cualquier caso si se forman  numeros con estos digitos, pero ay una exepcion, ke es cuando la suma de dos de las cifras de los dos numeros formados da un numero ke tiene decena y unidad (entre numeros con estos digitos, pero ay una exepcion, ke es cuando la suma de dos de las cifras de los dos numeros formados da un numero ke tiene decena y unidad (entre 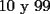 ), aqui pasa ke le tenemos ke restar ), aqui pasa ke le tenemos ke restar 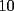 al numero al numero 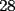 , porke se suprime la decena, que eslo mismo ke restarle , porke se suprime la decena, que eslo mismo ke restarle 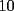 , y luego le sumamos , y luego le sumamos 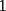 , por la reserva ke pasa por el borrado de la decena del numero anterior, de la sgte,. manera: , por la reserva ke pasa por el borrado de la decena del numero anterior, de la sgte,. manera: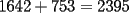 de esta manera cuando el se sumaron el  con el con el  , dio , dio 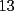 , y aqui se escribio el , y aqui se escribio el  , y se le sumo la reserva al , y se le sumo la reserva al 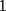 , y como vemos el resultado dio , y como vemos el resultado dio 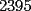 , donde la suma de sus cifras da , donde la suma de sus cifras da 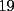 . Con la regla de divisibilidad del . Con la regla de divisibilidad del  , ke dice ke en un numero de , ke dice ke en un numero de  cifras, la suma de esas cifras, la suma de esas  cifras si da multiplo de cifras si da multiplo de  , es divisible por , es divisible por  , y como el , y como el 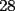 y el y el 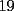 , ke son las posibilidades de las sumas de las cifras del numero ke se forma con los digitos del , ke son las posibilidades de las sumas de las cifras del numero ke se forma con los digitos del 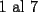 no es multiplo de no es multiplo de  , es imposible la solucion. , es imposible la solucion.responde por fa si esta bueno o no Veo que vamos mejorando las justificaciones pero aun asi solo dando un ejemplo no me convence que con cualquier combinacion no se pueda... Como una ayuda fijate que si miras un numero cualquiera Por ejemplo 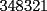 y lo divides por y lo divides por  y si tomas 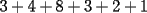 y lo divides por y lo divides por  ... ...Vuala...dejan el mismo resto(Comprobarlo en este caso y tratar de porque siempre es cierta esta propiedad) Ahora piensa en los numeros 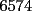 y y 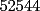 Fijate en que resto deja cada uno al dividir por  ,y suma esos restos...y a esa suma vuelve a dividirla por ,y suma esos restos...y a esa suma vuelve a dividirla por  y ve que resto deja y ve que resto dejaAhora intenta hacerlo sumando directamente 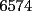 y y 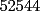 y a ese resultado dividelo por y a ese resultado dividelo por  . .Da lo mismo...? Es realmente asi siempre..que es lo que esta ocurriendo? Todas estas respuestas las puedes obtener en el sector de aprendizaje de fmat..en la parte de Congruencia Modulo... http://www.fmat.cl/index.php?showforum=77 Suerte y siguele intentando... Y te recomiendo que te registres...para asi ir creciendo en importancia dentro de fmat... Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Nov 20 2005, 04:20 PM Nov 20 2005, 04:20 PM
Publicado:
#37
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Michael @ Nov 20 2005, 05:04 PM) vamos a decir ke al ke le hicimos el problema penso un numero (n) el al agregar un  al numero ke penso, es como decir ke al numero ke penso, es como decir ke  es igual al es igual al 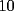 , y al numero ke le agrego el , y al numero ke le agrego el  es es 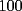 . Si pensamos hay ke restar el . Si pensamos hay ke restar el 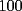 con el con el 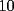 , y esto nos dio , y esto nos dio 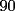 , ke esto es igual a , ke esto es igual a 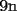 en una expresion algebraica. Luego pensamos ke la suma de las cifras del resultado de la resta es igual a un multiplo de en una expresion algebraica. Luego pensamos ke la suma de las cifras del resultado de la resta es igual a un multiplo de  , y ella al kitarle un digito, ke uede ser hasta , y ella al kitarle un digito, ke uede ser hasta  , sabremos ke le falta una cierta cantidasd para llegar a un multiplo de , sabremos ke le falta una cierta cantidasd para llegar a un multiplo de  mayor ke la suma de las cifras del resultado ke kedo al restarle la cifra. Por ejemplo: Penso el mayor ke la suma de las cifras del resultado ke kedo al restarle la cifra. Por ejemplo: Penso el 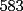 . . 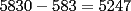 Luego: Luego: 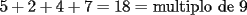 por ejemplo si le borro el 4 kedaria de la siguiente manera: 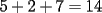 Luego: el multiplo de Luego: el multiplo de  mas cercano y mayor es mas cercano y mayor es 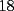 Como a 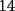 le faltan le faltan 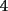 para llegar al para llegar al 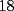 , se sabe ke , se sabe ke 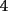 es el digito ke le borro. es el digito ke le borro. Esta justificacion me gusto mucho mas y esta correctisima...salvo que no explicaste porque se excluye eliminar alguna cifra igual a 0...pero de todas formas nada que decir..muy buena la solucion Felicidades y sigue participando..e insisto en que te registres Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Nov 21 2005, 04:06 PM Nov 21 2005, 04:06 PM
Publicado:
#38
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 21-November 05 Miembro Nº: 387 |
kenshin, ya me registre, me puse como darkblader. vale por invitarme.
|
|
|
|
 Nov 21 2005, 10:02 PM Nov 21 2005, 10:02 PM
Publicado:
#39
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 21-November 05 Miembro Nº: 387 |
la solu del problema 8:
Como tengo 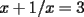 , si lo elevo al cubo, apareceran los terminos ke ando buscando. Para poder realizar la ecuacion, necesitare la piramide de pascal, y como la tercera linea de la piramide corresponde a un binomio elevado al cubo, diremos lo siguiente: , si lo elevo al cubo, apareceran los terminos ke ando buscando. Para poder realizar la ecuacion, necesitare la piramide de pascal, y como la tercera linea de la piramide corresponde a un binomio elevado al cubo, diremos lo siguiente: 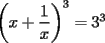 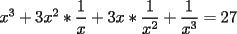 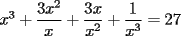 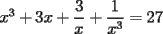 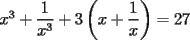 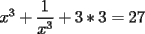 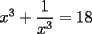 ... porque el 9 pasó restando al 27. ... porque el 9 pasó restando al 27. |
|
|
|
 Nov 21 2005, 10:08 PM Nov 21 2005, 10:08 PM
Publicado:
#40
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 21-November 05 Miembro Nº: 387 |
Para completar la respuesta de la pregunta 5, puedo decir ke otro numero ke puede dar de la suma de dos numeros formado por aquellos digitos, es el
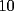 , en el caso de ke en la suma hayan 2 veces reservas, entonces podemos decir que , en el caso de ke en la suma hayan 2 veces reservas, entonces podemos decir que 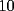 congruente con congruente con 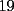 y congruente con y congruente con 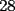 modulo3, ya ke daran todos resto modulo3, ya ke daran todos resto 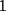 , entonces decimos ke es imposible formar dicho numero. , entonces decimos ke es imposible formar dicho numero. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 09:11 PM |











