|
|
|
|
|
|
|
  |
| Alvaro nawerwapi |
 May 13 2005, 05:29 AM May 13 2005, 05:29 AM
Publicado:
#11
|
|
Invitado |
5...
ya...jjajajaj oh me rei con la solucion de el seba...zephirox y ***....ta bien..pero en la parte tres pusiste cualquiier cosa.lo de los multplos de  ta super bien..de exo esa es la respuesta...por muxo q ordene y coloq los numeros siempre la suma los digitos va a dar ta super bien..de exo esa es la respuesta...por muxo q ordene y coloq los numeros siempre la suma los digitos va a dar 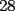 ....aparte cuando se suman numeros con reserva...esto me va a costar explikr...mm.....al pasar la reserva al lado izq(onda de unidades a decena.por ej)la suma total dada abajo,al suamr los dos digitos..."pierde" ....aparte cuando se suman numeros con reserva...esto me va a costar explikr...mm.....al pasar la reserva al lado izq(onda de unidades a decena.por ej)la suma total dada abajo,al suamr los dos digitos..."pierde"  unidades...por q el el resultado obtenido al suamr los dos digitos...cualesquiera q sea la combinacion,nunk va a ser multimpo de unidades...por q el el resultado obtenido al suamr los dos digitos...cualesquiera q sea la combinacion,nunk va a ser multimpo de  ...por q partiendo de ...por q partiendo de 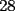 y "restando" y "restando"  nunk llegas a un numero en q la suma de los digitos q lo conforman sea multiplo de nunk llegas a un numero en q la suma de los digitos q lo conforman sea multiplo de  ... ...eso..ojala me entiendan... :cry: ....ya... seba demole y *** |
|
|
|
 May 13 2005, 05:30 AM May 13 2005, 05:30 AM
Publicado:
#12
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Hola nuevamente....
Lo que sucede es que si tu sumas 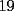 y y 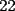 Y quieres sabes si esa suma es divisible en  , debes sacar su suma que es , debes sacar su suma que es 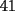 y luego hacer la suma de las cifras que es  ....tu lo haces en otro orden...sumas las cifras de una...antes de realizar la suma... ....tu lo haces en otro orden...sumas las cifras de una...antes de realizar la suma...Saludos David -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
| Alvaro nawerwapi |
 May 13 2005, 05:31 AM May 13 2005, 05:31 AM
Publicado:
#13
|
|
Invitado |
eee...ya eso lo del asunto...osea mi explikacion es la suma y despues el analisis...por ejemplo..en el mismo casoq diste tu...
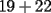 ....lo q hacia mi partner era sumar too altiro...y eso da ....lo q hacia mi partner era sumar too altiro...y eso da 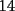 ... ...lo q dije yo..q al hacer la suma... 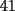 ahi recien hay q analizar si es divisible por ahi recien hay q analizar si es divisible por  ,tal como tu lo mencienas,si se fijan..."existe"una suma cn reserva y efectivamnte,como dije se "pierden" nuve unidades....por lo q la suma de los digitos es 5 a diferencia de lo de arriba q era ,tal como tu lo mencienas,si se fijan..."existe"una suma cn reserva y efectivamnte,como dije se "pierden" nuve unidades....por lo q la suma de los digitos es 5 a diferencia de lo de arriba q era 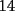 ...aparte...el problema de el tablero 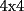 y los y los  y los y los 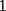 ...ganan las diagonales...o a la hacer mencion a filas te refieres soloa las horizontales?...genetalmnte es asi y columnas para las verticales...eso... ...ganan las diagonales...o a la hacer mencion a filas te refieres soloa las horizontales?...genetalmnte es asi y columnas para las verticales...eso...
|
|
|
|
 May 13 2005, 05:32 AM May 13 2005, 05:32 AM
Publicado:
#14
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Con respecto a tu duda...las filas siempre son horizontales...las columnas siempre vertiales(es cosa de pensar en la posicion de las columnas de un templo) y las diagonales no son ni filas ni columnas ^.^
Saludos...y sigan reflexionando... Hint: Lo que hicieron con eso de la suma divisible por 3 no esta del todo mal..muy por el contrario...lo que pasa es que hay algo que podrian demostrar....(traten de probar porque si la suma de las cifras de un numero es divisible por 3,entonces tb lo es el numero en si,quizas eso les daria una idea de como justificar algunas cosas...) |
|
|
|
| Alvaro nawerwapi |
 May 13 2005, 05:33 AM May 13 2005, 05:33 AM
Publicado:
#15
|
|
Invitado |
yaa..la demostracion de los multiplos de 3...jojojo
ya eee ..pongamos un numero formado por: 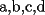 ......ya da lo mismo las cifras(cuantas sean) ......ya da lo mismo las cifras(cuantas sean)si tenemos que ... 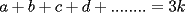 (*) (*)Queremos demostrar si el numero formado con esas cifras tambien es multiplo de  .... ....pongamonos en un caso corto...y veamos que es analogo para el resto de los casos... 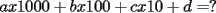 separemoslo convenientemente 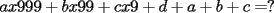 y eso... claramente por (*) es multiplo de  ...notemos tb q esto es independiente..tanto como del numero de cifras como del orden que coloquemos las mismas...ya eso....me voy a clases..jojojo ...notemos tb q esto es independiente..tanto como del numero de cifras como del orden que coloquemos las mismas...ya eso....me voy a clases..jojojochao |
|
|
|
 May 13 2005, 05:34 AM May 13 2005, 05:34 AM
Publicado:
#16
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Muy buena demostracion..pero aun no estas siendo explicito en como la aplicas..o sea insisto...
Tu si quieres ver si el numero 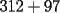 es o no divisible por es o no divisible por  ...lo que estas haciendo es sumar ...lo que estas haciendo es sumar 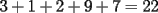 y ver si eso es divisible por y ver si eso es divisible por  (en realidad eso es efectivo..pero de eso quiero convencerme que entiendes a la perfeccion el porque ...) (en realidad eso es efectivo..pero de eso quiero convencerme que entiendes a la perfeccion el porque ...)O sea por el colegio para saber si 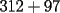 es o no es divisible por 3...lo que deberiamos haces es sumar primero,lo que nos da es o no es divisible por 3...lo que deberiamos haces es sumar primero,lo que nos da 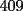 y luego sumar las cifras y dividir por y luego sumar las cifras y dividir por  .... ....O sea 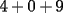 y eso da y eso da 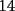 y deducir que el numero en este caso no es divisible por y deducir que el numero en este caso no es divisible por  ... ...Quiero en si que me justifiques basado en la demostracion que hiciste...que ambos razonamientos son correctos(notese que en un caso la suma nos da 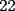 y en el otro caso nos dio y en el otro caso nos dio 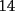 ,esa es la justificacion que yo espero...ademas de la demostracion que ya nos mandaste) ,esa es la justificacion que yo espero...ademas de la demostracion que ya nos mandaste)De verdad eres un joven muy aplicado..pero mi duda es...en que curso estas?....y donde estudias?....bueno...eso...y saludos Sigue asi ^.^ David -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
| MasterIN® |
 May 13 2005, 05:35 AM May 13 2005, 05:35 AM
Publicado:
#17
|
|
Invitado |
Ya...hola pos... bueno pase por aca... no habia visto esta sección, y voy a hacer una sol. cortita para el problema 10.
El asunto es que en la primera fila, los numeros del 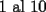 suman suman 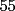 . .En la segunda, tb toos los numeros suman 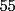 . Osea que la primera fila, mas la segunda fila suman . Osea que la primera fila, mas la segunda fila suman 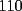 , por lo tanto, la suma de las unidades de la 3ra fila deberia ser , por lo tanto, la suma de las unidades de la 3ra fila deberia ser 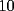 o un multiplo o un multiplo 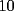 . . Sin embargo, nos damos cuenta que el problema nos dice que en la 3era fila las unidades deberian ser todas distintas, es decir, deberian estar las unidades desde el 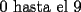 (no importa en que orden). Si suman esas unidades solamente, les da (no importa en que orden). Si suman esas unidades solamente, les da 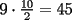 . Y como . Y como 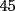 termina en termina en  y no en y no en  , significa que en la segunda fila es imposible que sean todas las unidades distintas, o sea que al menos una se deberia repetir. , significa que en la segunda fila es imposible que sean todas las unidades distintas, o sea que al menos una se deberia repetir.Ya pos...eso sería...chau no mas by 8) Master® |
|
|
|
| =))) |
 May 13 2005, 05:36 AM May 13 2005, 05:36 AM
Publicado:
#18
|
|
Invitado |
P2) ¿Tiene la ecuación
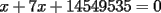 solucion para x en los enteros? solucion para x en los enteros? SOLU: 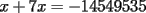 Sea  un entero par, por tanto un entero par, por tanto 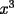 sigue siendo par , sigue siendo par , 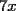 tambien , portanto jamas podria dar igual a una cantidad impar( tambien , portanto jamas podria dar igual a una cantidad impar(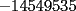 ). ).Sea x un entero impar , 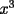 impar y impar y 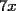 impar , impar mas impar es un par , por tanto jamas podria dar una igualdad con la susodicha cantidad impar( impar , impar mas impar es un par , por tanto jamas podria dar una igualdad con la susodicha cantidad impar(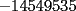 ). ).Se demuestra que la ecuacion no tiene soluciones enteras. Saludos , hasta pronto.... |
|
|
|
| =))) |
 May 13 2005, 05:37 AM May 13 2005, 05:37 AM
Publicado:
#19
|
|
Invitado |
P4)Un juego consiste de
 botones luminosos (de color verde o rojo) dispuestos formando un cuadrado de botones luminosos (de color verde o rojo) dispuestos formando un cuadrado de 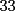 . Si se aprieta un botón del borde cambian de color él y todos sus vecinos, y si se aprieta el botón del centro cambian de color todos sus vecinos pero él no. ¿Es posible (apretando sucesivamente algunos botones) encender todas las luces con color verde, si inicialmente estaban todas encendidas con luz roja? Justifique la respuesta. . Si se aprieta un botón del borde cambian de color él y todos sus vecinos, y si se aprieta el botón del centro cambian de color todos sus vecinos pero él no. ¿Es posible (apretando sucesivamente algunos botones) encender todas las luces con color verde, si inicialmente estaban todas encendidas con luz roja? Justifique la respuesta.SOLU: Aunque paresca simple , la solucion del problema radica solo en darse cuenta de que cada vez que pulsamos un boton , un numero par de botones se transforman a un color , por tanto nunca se llenara de un solo color ya que  es impar. es impar.Adios ^^ |
|
|
|
 May 13 2005, 05:38 AM May 13 2005, 05:38 AM
Publicado:
#20
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Gracias Master IN y Cristobal pues sus aportes le han dado vida a esta parte del foro...se agradecen mucho sus excelentes soluciones...revisen las ediciones que hice en algunas de ellas..que les pueden servir de ayuda para ir perfeccionando aun mas sus explicaciones..que de verdad me han dejado demasiado contento...
Los felicito y me alegra conocer sus progresos... Saludos David ^.^ |
|
|
|
  |
3 usuario(s) está(n) leyendo esta discusión (3 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:20 PM |








