I2 Cálculo III - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Cálculo III

I2 Cálculo III, 1S 2011

Opciones

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	May 27 2011, 07:38 PM Publicado: #1
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent \\<br />\begin{center}MAT1630 - Cálculo III\\<br />Interrogación II - Miércoles 11 de Mayo de 2011 \end{center}<br />\begin{enumerate}<br />\item Dadas las funciones, <br /><br />$$\overrightarrow{G}(u, v) = (u, u^2, u\cos v), \overrightarrow{F}(x, y, z)=(x, xy, xyz),$$<br /><br />se considera la función compuesta $\overrightarrow{H}\equiv\overrightarrow{F}\circ\overrightarrow{G}=(H_1, H_2, H_3).$ Encontrar $\displaystyle\frac{\partial H_2}{\partial v}$ y $\displaystyle\frac{\partial H_3}{\partial u}$.<br /><br />\item Considere el sistema,<br /><br />$$x^2y+xe^v+u^2=4$$<br />$$x+2uv-vy=3$$<br /><br />\begin{enumerate}<br />\item Comprobar que existen funciones $u=u(x, y)$ y $v=v(x, y)$, definidas en una vecindad del punto $(0,1)$ tales que $u(0,1)=2, v(0,1)=1$ y que resuelven el sistema.<br /><br />\item Encuentre $\displaystyle\frac{\partial u}{\partial x}(0,1)$<br />\end{enumerate}<br /><br />\item <br />\begin{enumerate}<br />\item Sea $f(x,y)=x^2\|y\|$ y $R$ la región del plano interior al círculo $x^2+y^2=4$ y exterior a los círculos $x^2+(y-1)^2=1, x^2+(y+1)^2=1$. Calcule $\iint_R f(x,y)\ dx\ dy$.<br />\item Considere el tetraedro $T$ definido en $\mathbb{R}^3$ por los vértices $(0, 0, 0), (2, 0, 0), (0, 3, 0)$ y $(0, 0, 4)$. Calcular:<br /><br />$$\displaystyle\iiint_T x\ dx\ dy\ dz$$<br />\end{enumerate}<br /><br />\item Se considera el sólido $S$ descrito por:<br /><br />$$S=\{(x,y,z)\in\mathbb{R}^3: z\in[0, 1], x^2+y^2-2x(1-z)\le{0}.$$<br /><br />\end{enumerate}<br />$ $TEX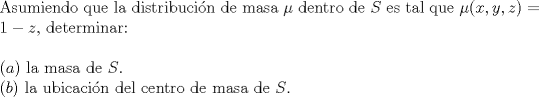: <br /><br />\noindent Asumiendo que la distribución de masa $\mu$ dentro de $S$ es tal que $\mu(x,y,z) = 1-z$, determinar:\\<br /><br />\noindent $(a)$ la masa de $S$.\\<br />$(b)$ la ubicación del centro de masa de $S$.<br /><br /><br />$ -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)