|
|
|
|
|
|
|
  |
 May 14 2011, 11:48 PM May 14 2011, 11:48 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987 |
IX CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT Fecha 2: Sábado 14 de Mayo de 2011 Cuarto Nivel Individual Problema 1 Sea ![TEX: \[<br />ABCD<br />\]](./tex/7162f4499cdbfe60b8c0e20de72c9844.png) un cuadrado y un cuadrado y ![TEX: \[<br />P,Q<br />\]](./tex/badb562dc6bb934d38ad3912c2caa882.png) puntos distintos en su interior, tales que puntos distintos en su interior, tales que ![TEX: \[<br />AP = BP = PQ = CQ = DQ = 10<br />\]](./tex/300f63c814cff3ba9c6d035f34786203.png) . . Encuentre la longitud del Lado del Cuadrado. Problema 2 Pruebe que si ![TEX: \[<br />a,b > 0<br />\]](./tex/d715d7afee22355e1cb606ee7b1825a5.png) son tales que son tales que![TEX: \[<br />\left( {\forall n \in \mathbb{N}} \right)\left( {\left\lfloor {10^n a} \right\rfloor - 10\left\lfloor {10^{n - 1} a} \right\rfloor > \left\lfloor {10^n b} \right\rfloor - 10\left\lfloor {10^{n - 1} b} \right\rfloor } \right) \Rightarrow \left( {\left\{ a \right\} \geqslant \left\{ b \right\} + \frac{1}<br />{9}} \right)<br />\]](./tex/54bc8a8b2305c721c2d9bb5fed33b749.png) Donde ![TEX: \[<br />\left\lfloor x \right\rfloor <br />\]](./tex/5e3a1a9758f82d68260211aa73b221de.png) es la parte entera de es la parte entera de ![TEX: \[<br />x<br />\]](./tex/080180eb79674b4a9f233212148e3aab.png) , y , y ![TEX: \[<br />\left\{ x \right\}<br />\]](./tex/e38f22e503efda4fd9da50b3f0de8930.png) es la parte decimal de es la parte decimal de ![TEX: \[<br />x<br />\]](./tex/e662988166876d841345a2923fc28e42.png) ( (![TEX: \[<br />\left\lfloor x \right\rfloor + \left\{ x \right\} = x<br />\]](./tex/917cfbe3ed0aeb079b7ab296552c454d.png) ) )Salu2. PD: No puedo subir los demas niveles debido a que no los tengo -------------------- CHAO.
|
|
|
|
 May 14 2011, 11:57 PM May 14 2011, 11:57 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.648 Registrado: 16-April 10 Desde: Dalcahue-Chiloe Miembro Nº: 68.853 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Buena loco, la estaba esperando !!!!!!!!!!!!!!!!!!
Mensaje modificado por Gerardo Soto el May 14 2011, 11:57 PM -------------------- >>He robado princesas a reyes agónicos. Incendié la ciudad de Trebon. He pasado la noche con Felurian y he despertado vivo y cuerdo.
Me expulsaron de la Universidad a una edad a la que a la mayoría todavía no los dejan entrar. He recorrido de noche caminos de los que otros no se atreven a hablar ni siquiera de día. He hablado con Dioses, he amado a mujeres y he escrito canciones que hacen llorar a los bardos.<< <<Me llamo Kvothe (<Cuouz>). Quizá hayas oído hablar de mí.”>> El nombre del viento, primer dìa de la historia de Kvothe .-“Todo hombre sabio le teme a tres cosas: Una noche sin luna, una tormenta en el mar y a la ira de un hombre bueno.”” Citas del Nombre del viento Para saber más de la trilogía de Patrick Rothfuss Click aquí |
|
|
|
 May 15 2011, 12:18 AM May 15 2011, 12:18 AM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 31-May 10 Desde: San antonio Miembro Nº: 71.730 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sean
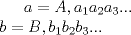 luego 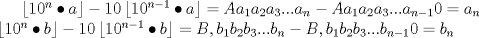 de aquí se desprende que para cualquier valor 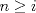 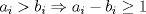 entonces 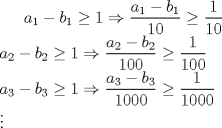 sumando las desigualdades 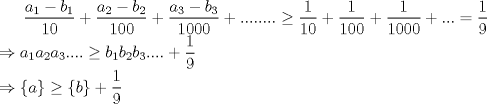 Saludos C: Mensaje modificado por luis_fz el May 15 2011, 12:34 AM |
|
|
|
 May 15 2011, 12:26 AM May 15 2011, 12:26 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.689 Registrado: 5-September 10 Desde: villarrica Miembro Nº: 76.659 Nacionalidad:  Sexo:  |
Problema 1:
el segmento PQ pasa por el centro del cuadrado dividiendolo en dos rectangulos congruentes. trazando los segmentos AP yBP, CQ y DQ, se forman dos triagulos y dos trapecios isosceles. mediante pitagoras me da que el lado del rectangulo es ![TEX: \[<br />5(\sqrt 7 + 1)<br />\]<br />](./tex/9de3aa0ce91f3a6af6a730be4100b999.png) PD: Disculpen que aun no se adjuntar imagenes. Si esta mal me avisan.... |
|
|
|
 May 15 2011, 12:43 AM May 15 2011, 12:43 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
^ Ese es el resultado pero no tan rápido, explica como lo haces pues la figura no está para llegar y hacerlo.
Saludos. Mensaje modificado por El Geek el May 15 2011, 12:53 AM -------------------- Me voy, me jui.
|
|
|
|
 May 15 2011, 02:12 AM May 15 2011, 02:12 AM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 274 Registrado: 20-May 10 Miembro Nº: 71.064 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
  Saludos P.D: tuve problemas para subir la imagen. Trataré de subirla en un rato más. Mensaje modificado por sushi_8 el May 15 2011, 04:47 AM -------------------- 100% REAL NO FAKE 1 LINK MEGAUPLOAD KEYGEN + CRACK FULL HD 1080P SUBS ESPAÑOL [PORTABLE]
|
|
|
|
 May 15 2011, 03:17 AM May 15 2011, 03:17 AM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Hola sushi, discrepo con tu resultado. Mira, prolonga AP hasta que intersecte al lado BC en
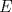 . Y digamos que . Y digamos que  y y 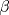 son ángulos complementarios y como son ángulos complementarios y como 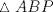 es isósceles de base es isósceles de base 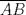 entonces entonces 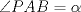 . Bien, ahora como el . Bien, ahora como el 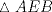 es rectángulo, entonces el es rectángulo, entonces el 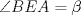 pues pues  y y 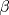 son complementarios. Ahora bien, como el trapecio son complementarios. Ahora bien, como el trapecio 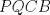 es isósceles, entonces es isósceles, entonces  , por lo que el cuadrilátero , por lo que el cuadrilátero 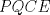 es paralelógramo, con lo que podemos deducir que es paralelógramo, con lo que podemos deducir que  . .Ahora bien, sea $a$ el lado del cuadrado, entonces 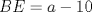 , lo que nos permite establecer el siguiente Pitagorazo: , lo que nos permite establecer el siguiente Pitagorazo: ![TEX: $AB^2 + BE^2 = AE^2 \Rightarrow a^2 + (a-10)^2 = 20^2 \therefore a = 5 + 5 \cdot \sqrt[2]{7} $](./tex/1d1529194b9161755cee7ff3b97606b7.png) Saludos -------------------- Me voy, me jui.
|
|
|
|
 May 15 2011, 04:44 AM May 15 2011, 04:44 AM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 274 Registrado: 20-May 10 Miembro Nº: 71.064 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Hola sushi, discrepo con tu resultado. Mira, prolonga AP hasta que intersecte al lado BC en 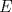 . Y digamos que . Y digamos que  y y 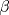 son ángulos complementarios y como son ángulos complementarios y como 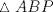 es isósceles de base es isósceles de base 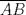 entonces entonces 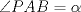 . Bien, ahora como el . Bien, ahora como el 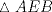 es rectángulo, entonces el es rectángulo, entonces el 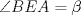 pues pues  y y 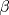 son complementarios. Ahora bien, como el trapecio son complementarios. Ahora bien, como el trapecio 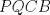 es isósceles, entonces es isósceles, entonces  , por lo que el cuadrilátero , por lo que el cuadrilátero 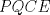 es paralelógramo, con lo que podemos deducir que es paralelógramo, con lo que podemos deducir que  . .Ahora bien, sea $a$ el lado del cuadrado, entonces 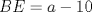 , lo que nos permite establecer el siguiente Pitagorazo: , lo que nos permite establecer el siguiente Pitagorazo: ![TEX: $AB^2 + BE^2 = AE^2 \Rightarrow a^2 + (a-10)^2 = 20^2 \therefore a = 5 + 5 \cdot \sqrt[2]{7} $](./tex/1d1529194b9161755cee7ff3b97606b7.png) Saludos asdsd xd, a la hora de editar me olvide de copiar la última línea que era el mismo resultado que tienes tu xd. Edito de inmediato xd. -------------------- 100% REAL NO FAKE 1 LINK MEGAUPLOAD KEYGEN + CRACK FULL HD 1080P SUBS ESPAÑOL [PORTABLE]
|
|
|
|
 May 15 2011, 02:08 PM May 15 2011, 02:08 PM
Publicado:
#9
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 341 Registrado: 8-November 09 Desde: Santiago de Chile Miembro Nº: 61.684 Nacionalidad:  Universidad:  Sexo:  |
Hola sushi, discrepo con tu resultado. Mira, prolonga AP hasta que intersecte al lado BC en 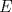 . Y digamos que . Y digamos que  y y 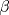 son ángulos complementarios y como son ángulos complementarios y como 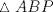 es isósceles de base es isósceles de base 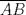 entonces entonces 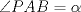 . Bien, ahora como el . Bien, ahora como el 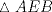 es rectángulo, entonces el es rectángulo, entonces el 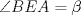 pues pues  y y 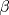 son complementarios. Ahora bien, como el trapecio son complementarios. Ahora bien, como el trapecio 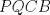 es isósceles, entonces es isósceles, entonces  , por lo que el cuadrilátero , por lo que el cuadrilátero 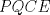 es paralelógramo, con lo que podemos deducir que es paralelógramo, con lo que podemos deducir que  . .Ahora bien, sea $a$ el lado del cuadrado, entonces 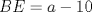 , lo que nos permite establecer el siguiente Pitagorazo: , lo que nos permite establecer el siguiente Pitagorazo: ![TEX: $AB^2 + BE^2 = AE^2 \Rightarrow a^2 + (a-10)^2 = 20^2 \therefore a = 5 + 5 \cdot \sqrt[2]{7} $](./tex/1d1529194b9161755cee7ff3b97606b7.png) Saludos -------------------- Para llegar a ser sabio, es preciso querer experimentar ciertas vivencias, es decir, meterse en sus fauces. Eso es, ciertamente, muy peligroso; más de un sabio ha sido devorado al hacerlo. Friedrich Nietzsche
kallensky |
|
|
|
 May 15 2011, 05:05 PM May 15 2011, 05:05 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Cabros, ahora subiré las otras pruebas (las tengo porque fui como examinador). -------------------- Me voy, me jui.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 12th April 2025 - 06:58 AM |









