|
|
|
|
|
|
|
  |
 May 10 2011, 11:58 PM May 10 2011, 11:58 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Control N°4 Geometria - MAT1305
Problema 1: Considere las rectas 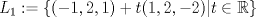 y y 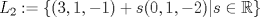 a) Demuestra que 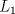 y y 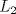 tienen intersección vacía. tienen intersección vacía.b) Encuentra la ecuación del plano  que contiene a que contiene a 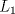 y una recta paralela a y una recta paralela a 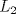 . .c) Considera 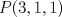 , y encuentra su proyección ortogonal a , y encuentra su proyección ortogonal a  Problema 2: Sean 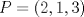 y y 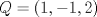 . Encuentra la ecuación del plano . Encuentra la ecuación del plano  tal que para todo tal que para todo 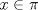 se cumple que se cumple que 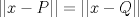 . .Problema 3: Sea 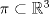 un plano y un plano y 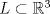 una recta. Demuestre que una y solo una de las siguientes afirmaciones se cumple: una recta. Demuestre que una y solo una de las siguientes afirmaciones se cumple:
-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th April 2025 - 06:43 PM |





 es vacío.
es vacío. consiste de un único punto.
consiste de un único punto.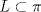 .
.

