C3 Geometría I (MAT1305)

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Geometría

C3 Geometría I (MAT1305), Vectores

Opciones

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	May 10 2011, 11:20 PM Publicado: #1
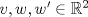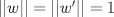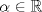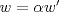Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Control N°3 Geometria - MAT1305 Sean $TEX: $v, w,w'\in \mathbb {R}^2$$ tales que $TEX: $\|\|w\|\|=\|\|w'\|\|=1$$ y que no existe $TEX: $\alpha \in \mathbb{R}$$ tal que $TEX: $w=\alpha w'$$ . 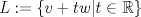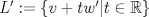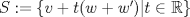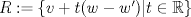Defina las rectas $TEX: $L:=\{v+tw\|t\in \mathbb {R}\}$$ , $TEX: $L':=\{v+tw'\|t\in \mathbb {R}\}$$ , y sean $TEX: $S:=\{v+t(w+w')\|t\in \mathbb {R}\}$$ y $TEX: $R:=\{v+t(w-w')\|t\in \mathbb {R}\}$$ . 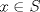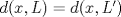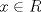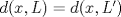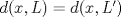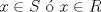a) Demuestre que si $TEX: $x\in S$$ , entonces $TEX: $d(x, L)=d(x, L')$$ b) Demuestre que si $TEX: $x\in R$$ , entonces $TEX: $d(x, L)=d(x, L')$$ c) Demuestre que si $TEX: $x$$ es tal que $TEX: $d(x,L)=d(x, L')$$ , entonces $TEX: $x\in S$ ó $x\in R$$ . Mensaje modificado por ~Fatal_Collapse~ el May 22 2011, 03:59 PM -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2013, 10:28 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	Outline: Para cada real t, el triángulo formado por L(t), L'(t) y O=(0,0) es isósceles así que al completar el paralelógramo obtendremos un rombo que como sabemos tiene sus diagonales perpendiculares y son bisectrices del correspondiente ángulo interior. Aplicamos esto al problema y "casi" no hay nada que calcular para hacer una demostración elegante y desde una perspectiva puramente geométrica, trolleando así los objetivos evidentes de la prueba -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Cenizas con Most... Cenizas con Mostaza Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2013, 11:35 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad: Universidad: Sexo:	CITA(Kaissa @ Aug 4 2013, 10:28 PM) Outline: Para cada real t, el triángulo formado por L(t), L'(t) y O=(0,0) es isósceles así que al completar el paralelógramo obtendremos un rombo que como sabemos tiene sus diagonales perpendiculares y son bisectrices del correspondiente ángulo interior. Aplicamos esto al problema y "casi" no hay nada que calcular para hacer una demostración elegante y desde una perspectiva puramente geométrica, trolleando así los objetivos evidentes de la prueba Nice -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass!

« Posterior · Geometría · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 05:03 AM